Au lycée en terminale scientifique : Une figure sur la loi normale N(0,1)

Pour faire cette figure, téléchargez la version 4.7 ou ultérieure de MathGraph32.

f est la fonction définie sur R par $f(t)=\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}}$ , fonction de densité de la loi normale N(0, 1) sur R.

Si X est une variable aléatoire suivant la loi normale N(0, 1), pour tout réel $\alpha$ de l’intervalle ]0 ; 1], il existe un unique réel $u_\alpha$ de R tel que $P(-u_\alpha \le X \le u_\alpha)=1-\alpha$.

Soit g la fonction définie sur R par $g(x) = \int_0^x {f(t)dt}$ .

Si x est un réel positif, $P( - x \le X \le x) = \int_{ - x}^x {f(t)dt} = 2\int_0^x {f(t)dt} = 2g(x)$.

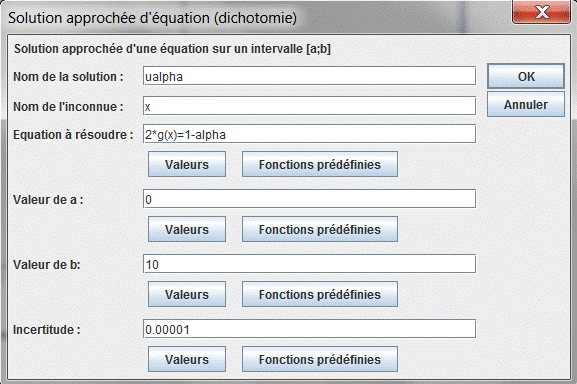
$u_\alpha$ est donc la solution positive de l’équation $2g(x) = 1 - \alpha$.

Utilisation de MathGraph32 pour calculer et représenter $u_\alpha$

Utilisez l’icône et choisissez un repère orthogonal avec pointillés sans vecteurs
.
Capturez l’origine O pour l’emmener en bas de la figure et le point J sur l’axe des ordonnées pour augmenter l’unité sur l’axe des abscisses.

Activez le style de trait continu épais dans la palette de style de trait.

Utilisez l’icône pour créer la fonction de densité :
–  Dans le champ nom de la fonction entrez f.
–  Dans le champ Variable formelle, entrez t.
–  Dans le champ Formule, entrez 2*exp(t)/sqrt(2*pi).
–  Laissez cochée la case Tracer courbe et validez.
La courbe de la fonction apparaît.

De nouveau, utilisez l’icône pour créer la fonction g.
–  Dans le champ Nom de la fonction entrez g.
–  Dans le champ Variable formelle, entrez x.
–  Dans le champ Formule, entrez 2*integrale(f(t),t,0,x).
–  Cette fois décochez la case Tracer courbe et validez.

Dans la palette de style de trait, activez le style fin continu.
Pour faire varier $u_{\alpha}$ nous allons utiliser un curseur. Utilisez l’icône pour créer un curseur en haut et à gauche de la figure.
Dans la boîte de dialogue de création du curseur :
–  Dans le champ Valeur mini, entrez 0.0001.
–  Dans le champ Valeur maxi, entrez 1.
–  Dans le champ Nom du calcul représentant le curseur, entrez alpha.
–  Dans le champ Affichage précédé de, entrez $\alpha=$
–  Dans le champ Affichage suivi de, entrez $ (les signes $ de début et de fin servent à utiliser le style LaTeX).
–  Validez.

Calculons maintenant une valeur approchée de $u_\alpha$.
Pour cela utilisez le menu Calculs – Nouveau calcul dans R - Solution approchée d’équation.

Remplissez la boîte de dialogue comme ci-dessous puis validez.

Cliquez ensuite sur l’icône d’affichage de valeur libre.
Cliquez au-dessous du curseur puis remplissez la boîte de dialogue comme ci-dessous :

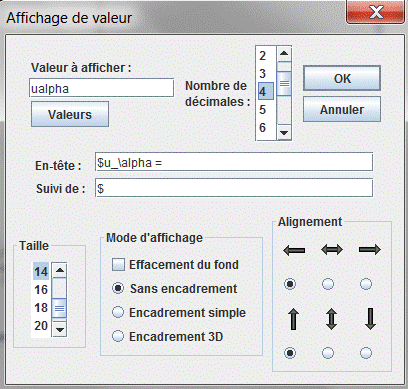
Là encore on utilise le style d’affichage LaTeX.
Utilisez maintenant l’icône pour créer le point de coordonnées (ualpha,0) et (- ualpha,0).

Nous allons maintenant hachurer l’aire sous la courbe correspondant à la probabilité .

Pour cela nous devons d’abord tracer la courbe de la fonction f sur l’intervalle $\left[ { - u_\alpha ;u_\alpha } \right]$ .
Utilisez l’icône de création de courbe. Dans la boîte de dialogue qui s’ouvre, cliquez sur l’icône ][a ;b][ pour tracer une courbe sur un intervalle. Remplissez la boîte de dialogue comme ci-dessous :

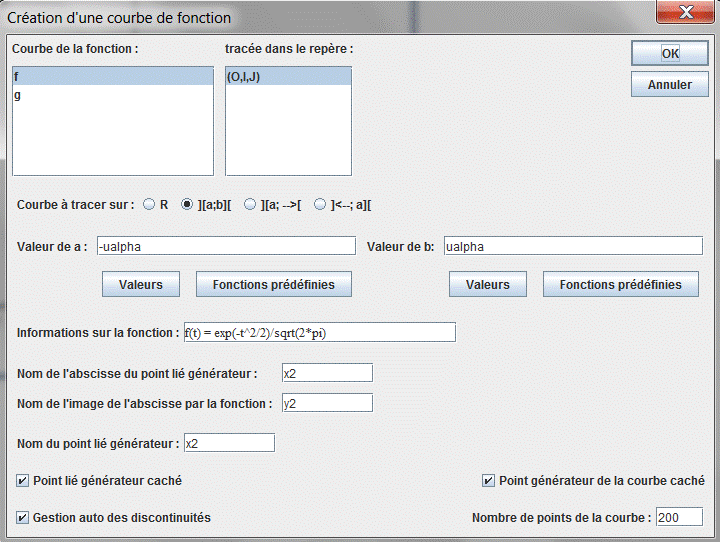
Dans la palette de couleurs activez la couleur bleue.
Maintenant activez l’icône qui sert à créer une surface délimitée par un lieu de points et une droite.

Cliquez sur la courbe (il faudra préciser que c’est le dernier objet qu’on utilise, il s’agit pour le logiciel d’un lieu de points) puis sur l’axe des abscisses.

Maintenant utilisez l’icône pour masquer la courbe qui nous a servi à créer cette surface.
Pour finir, utilisez l’icône pour créer un affichage LaTeX lié au point de coordonnées .
Dans le champ Code LaTeX, entrez u_\alpha.

De même créez un affichage LaTeX lié au point de coordonnées $\left( { - u_\alpha ;0} \right)$ avec comme code LaTeX : - u_\alpha.

Voici la figure terminée (en html5 animée avec le moteur javaScript de MathGraph32) :