Exemple 2 niveau Lycée (version Java) : Illustration d’une propriété des intégrales.

Nous souhaitons créer la figure ci-dessous (animée par le moteur JavaScript de MathGraph32). Vous pouvez y capturer les points a et b.

Vérifiez que le logiciel utilise bien le radian comme unité d’angle pour les nouvelles figures (menu Options >> Préférences, onglet Unité d’angle).

Créez une nouvelle figure munie d’un repère orthogonal (par exemple) avec le menu Utilisez l’icône de la barre supérieure.

Utilisez l’icône pour créer une nouvelle fonction réelle nommé f définie par f(t)=sin(pi*t)^2+cos(pi*t)+1. Pour cela, entrez f dans le champ Nom de la fonction, t dans le champ Variable formelle et entrez dans le champ Formule sin(pi*{t})^2+cos(pi*{t})+1. Laissez cochée la case Tracer courbe et demandez 500 points.

La courbe apparaît. Un point lié à l’axe des abscisses a été créé automatiquement nommé x. Un nouveau calcul a été créé nommé y et contenant comme formule f(x) puis un point de coordonnées (x ;f(x)). La courbe a été créée comme lieu de ce nouveau point. Vous pouvez utiliser la touche F5 appelant la boîte de dialogue d’historique pour voir tous les objets créés pour vous en créant cette courbe.

Dans la palette des couleurs, activez la couleur bleue.

Créez un point lié à l’axe des abscisses (outil et nommez-le a (outil ).

Pour mesurer l’abscisse de ce point utilisez l’icône
Un message vous prévient que cette abscisse est nommée xCoord(a,O,I,J)).

Créez maintenant avec l’outil un calcul nommé a contenant comme formule xCoord(a,O,I,J) (utilisez le bouton Liste des valeurs]. a contient donc notre abscisse précédemment mesurée.

Créez le point de coordonnées (a + 2 ; 0) (outil ).

Nous allons maintenant créer un commentaire (texte) lié à ce dernier point. Utilisez pour cela l’icône . Cliquez sur le dernier point créé. Une boîte de dialogue s’ouvre. Entrez comme texte du commentaire : a + 2 et validez. Ce commentaire se déplacera avec le point auquel il est lié. Vous pouvez utiliser l’outil pour changer sa position relative par rapport à ce point.

Nous allons maintenant créer la courbe représentative de f sur l’intervalle [a ; a + 2] à l’aide de l’icône .

Dans la boîte de dialogue qui s’ouvre, cochez la case Courbe à tracer sur [a ; b]. Complétez cette boîte comme ci-dessous.

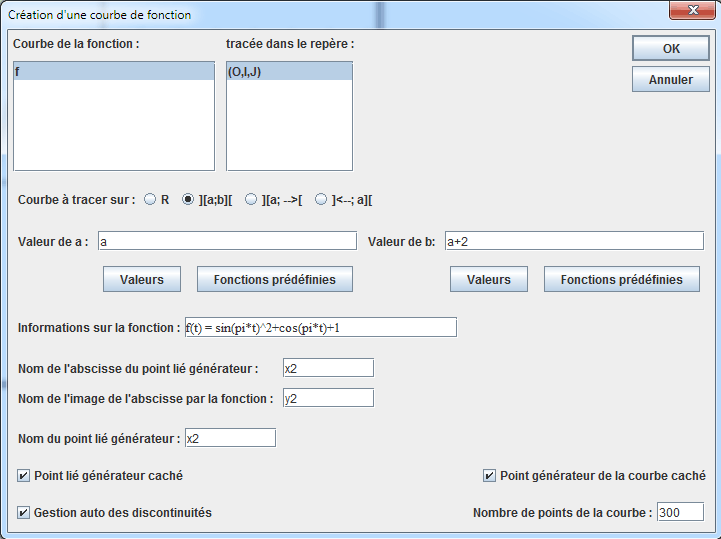
Dans la palette de style de remplissage choisissez le style de hachure . Utilisez l’icône pour hachurer la surface comprise entre la dernière courbe et l’axe des abscisses (cliquez d’abord sur la courbe qui est un lieu de points puis sur l’axe des abscisses). Il vous sera demandé quel lieu d’objets vous voulez désigner, premier ou dernier. Il s’agit du dernier.

Créez ensuite les points de coordonnées (a ; f(a)) et (a + 2 ; f(a + 2)) (outil et joignez en pointillé par des segments les points de coordonnées (a ; 0) et (a ; f(a)) et (a + 2 ; 0) et (a + 2 ; f(a + 2)).

Masquez ensuite la courbe de f sur l’intervalle [a ; a + 2] (outil ). Il s’agit du dernier lieu de points).

Dans la palette de couleurs, activez la couleur verte.

Créez un nouveau point lié à l’axe des abscisses que vous nommerez b, mesurez son abscisse dans notre repère, créez un nouveau calcul nommé b contenant cette abscisse, et la courbe représentative de f sur l’intervalle [b ;b + 2].

Dans la palette de style de remplissage choisissez le style de remplissage avec effet de transparence.

Cliquez sur l’outil de choix de couleur personnalisée. Une boîte de choix de couleur personnalisée s’ouvre. Choisissez une couleur verte très claire et validez.

Procédez de même que précédemment pour remplir la surface comprise entre la courbe de f sur l’intervalle [b ;b + 2] et l’axe des abscisses.

Améliorons encore notre figure pour illustrer que notre fonction est périodique de période 2.

Dans la palette de couleurs activez la couleur noire et dans la palette de style de trait activez le trait épais.

Cliquez sur l’icône de création d’un vecteur. Cliquez successivement sur les points de coordonnées (a ; f(a)) et (a + 2 ; f(a + 2)).

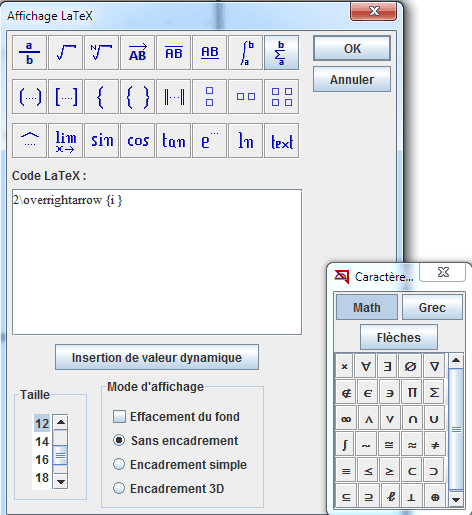
Créons maintenant un affichage de code LaTeX spécial lié au deuxième de ces points pour afficher $2\vec i$ au voisinage du point. Pour cela utilisez l’icône et cliquez sur le point de coordonnées (a + 2 ; f(a + 2)). Une boîte de dialogue s’ouvre. Dans le champ texte du commentaire, entrez 2 puis cliquez sur l bouton . Complétez le code LaTeX comme ci-dessous et validez.

Vous pouvez utiliser l’outil pour changer la position relative du commentaire par rapport au point.