A library on conics

Thanks to Luis Belcredi a library of constructions on conics is available.

This article has been adapted to the JavaScript version of MathGraph32.

If not already done, download predefined MathGraph32 on this page or underneath. Unzip the file in the directory of your choice.

In Mathgraph32, conics are not native objects. In this library they will be emulated as point locuses.

Here is a simple example using this library.

Create a new empty figure with icon and 5 free points with icon .

In the upper toolbar, use icon making available more tools to manage constructions.

Use icon (constructions management) and choose item Incorporate construction from file. Browse to the directory you unzipped the construction zip file to. Open the directory conics and select the construction named Conic Through 5 points then click on button Open. This construction is now part of your figure.

Again use icon and select item Implement a construction of the figure. In the list, the only available construction is already selected. Click on button Implement like underneath.

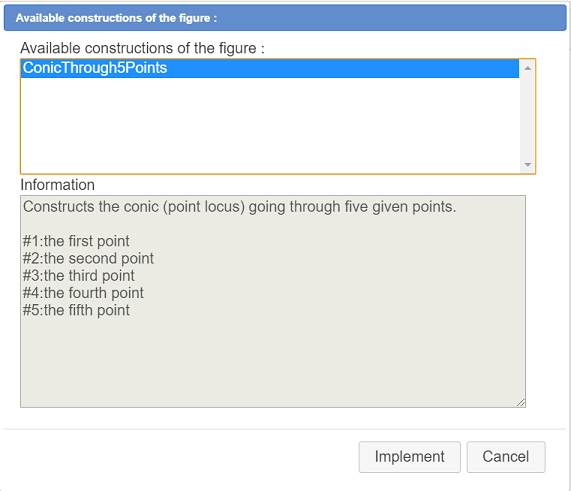
Then click on the 5 points.

The conic appears (In fact a point locus generated by the macro construction).

Now use icon and create a point linked to the conic (in fact the point locus).

Again use icon , activate item Incorporate a construction from file. In the directory Conics, click on the construction named Tangent to conic At point. This new construction is now part of your figure.

Click again on icon and activate item Implement a construction of the figure figure. This time select the construction TangentToConicAtPoint then click on button Implement as underneath.

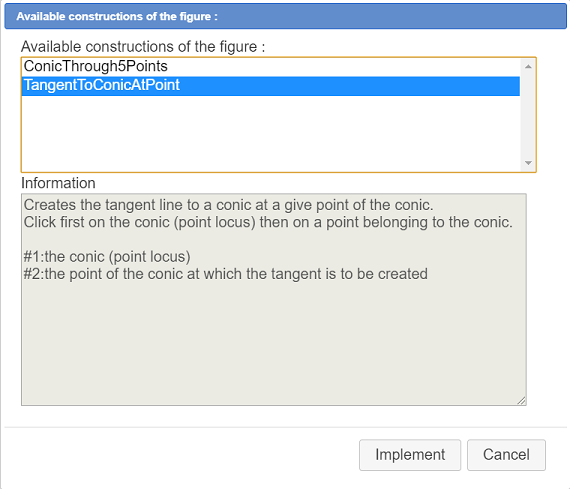
Click on the conic then on the linked point. The tangent appears.

Underneath you can see the figure. You can capture all the six points.