Exemple d’utilisation avancée du calcul dans MathGraph32 : La courbe du blancmange

Dans cet article je vais montrer comment illustrer ce TP du livre de Terminale S édité par les éditions Magnard, premier livre de terminale S libre sous licence CC by SA.

L’association Sesamath s’est chargée des relectures et des compléments numériques de ce manuel.

Le TP que nous allons illustrer est le TP page 114 (récréations et énigmes). Vous remarquerez la petite icône Mg qui indique qu’une figure MathGraph32 est disponible. Il suffit de cliquer sur cette icône pour que la figure se lance dans votre navigateur. Celle-ci est disponible pour les élèves, d’autres nécessitent que le professeur soit connecté avec son compte Sesaprof).

Il s’agit donc de créer une approximation graphique de la fonction blanc définie sur R par $blanc(x)=\sum_{n=0}^{+\infty}\frac{1}{2^k}\left| 2^kx-\left[ 2^kx+\frac{1}{2} \right] \right|$ où [x] désigne la partie entière du réel x.

Les explications ci-dessous se réfèrent à la version JavaScript de MathGraph32 (version 5.5.4 ou ultérieure). Vous pouvez l’utiliser en ligne sur cette page.

Commençons par créer une nouvelle figure munie d’un repère orthonormal avec l’icône . Choisissez Figure avec repère . Demandez un repère non quadrillé et sans graduations.

A l’aide de l’icône de capture, emmenez l’origine O du repère en bas et à gauche de la figure et éloignez ensuite le point I du point O comme sur la figure en bas de cet article.

Nous allons maintenant créer un curseur à valeurs entières dont les valeurs seront nommées k à l’aide d l’icône .

Cliquez en haut et à gauche de la figure (ce sera l’extrémité gauche du curseur) et renseignez la boîte de dialogue comme ci-dessous (#I sert à passer en italiques et #N à revenir en affichage normal).

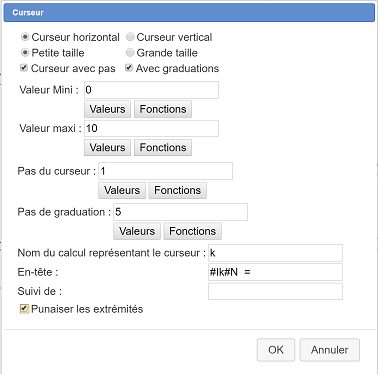
Vous pouvez agrandir la taille de police de l’affichage de la valeur du curseur en cliquant sur cet affichage avec l’outil de modification d’objet graphique.

Créons maintenant créer une fonction de deux variables g.

Pour cela déroulez la barre d’icônes des calculs et cliquez sur l’icône et choisissez Fonction réelle de deux variables. La formule à entrer pour g est donc 1/2^n*abs(2^n*x-int(2^n*x+1/2)).

Renseignez la boîte de dialogue comme ci-dessous :

Poursuivons à l’aide de l’icône en créant la fonction fk définie par $f_k(x)=\frac{1}{2^k}\left| 2^kx-\left[ 2^kx+\frac{1}{2} \right] \right|$.

Dans la palette de couleurs activez la couleur violette puis utilisez l’icône (en déroulant la barre d’icônes horizontale initialement représentée par le curseur). Renseignez la boîte de dialogue comme ci-dessous :

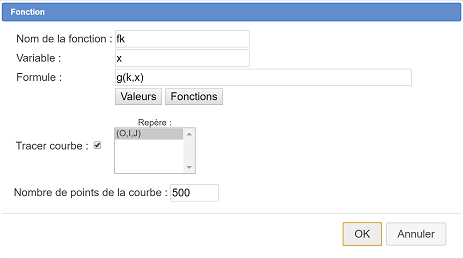
La représentation graphique de fk apparaît. Si vous capturez le curseur à l’aide de l’icône vous voyez cette courbe s’actualiser.

Nous allons maintenant créer la fonction f (approximation de la fonction de la fonction blanc qui sera la somme des fonctions fk pour k variant de 0 à 10.

Dans la palette de couleurs activez la couleur bleue.

Utilisez l’icône . Renseignez la boîte de dialogue comme ci-dessous :

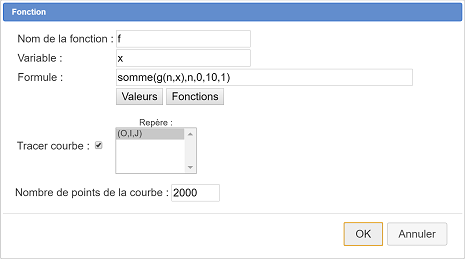
A noter qu’ici nous demandons 2000 points car cette courbe est très découpée et que si on clique dans la boîte de dialogue sur Fonctions prédéfinies on peut voir la fonction somme et une indication sur sa syntaxe.

Pour montrer comment se fait l’approximation nous allons créer une dernière fonction h et sa courbe représentative.

Dans la palette de couleurs activez la couleur verte.

Utilisez l’icône . Renseignez la boîte de dialogue comme ci-dessous :

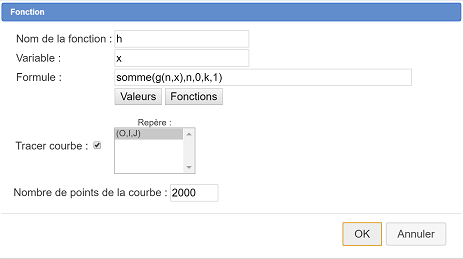
Faites maintenant varier la valeur de k en capturant le point curseur (icône ).

Pour finir nous pouvons créer en haut de la figure trois affichages LaTeX dans les couleurs associées aux courbes correspondantes (outil ). Pour cela vous pouvez utiliser les boutons qui permettent de créer le code LaTeX qui n’a plus qu’à être complété par vos soins.

Voici le code complet de chacun de ces trois affichages :

f_k(x)=\frac{1}{2^k}\left| 2^kx-\left[ 2^kx+\frac{1}{2} \right] \right|

f(x)=\sum_{n=0}^{10}f_n(x)

g(x)=\sum_{n=0}^{k}f_n(x)

Et voici ci-dessous la figure dynamique animée par le moteur JavaScript de MathGraph32.