Toutes les versions de cet article : [Español] [français]
Un collègue (merci Thomas) m’ayant fait connaître cette vidéo : https://www.youtube.com/watch?v=-X49VQgi86E , j’ai eu l’idée de faire une figure dynamique pour illustrer ces résultats.
L’idée est la suivante, n et p étant des entiers naturels au moins égal à 2 :
On représente chacun des entiers k compris entre 0 et n - 1 par des points régulièrement espacés sur un cercle.
Pour chaque entier k compris entre 0 et n - 1, on relie par un segment le point associé à k et le point associé à $k \times p$.
Nous ferons cette figure avec la nouvelle version JavaScript de MathGraph32 que vous pouvez télécharger sur cette page ou utiliser en ligne sur cette page.
Démarrez le logiciel et utilisez l’icône ![]() permettant de créer une nouvelle figure. Choisissez une figure sans repère et sans longueur unité (pour ce type de figure l’unité d’angle est le degré).
permettant de créer une nouvelle figure. Choisissez une figure sans repère et sans longueur unité (pour ce type de figure l’unité d’angle est le degré).
A l’aide de l’outil ![]() , créez un point libre que nous appellerons O (entrez le nom dans l’éditeur qui apparaît sur la figure une fois le point créé).
, créez un point libre que nous appellerons O (entrez le nom dans l’éditeur qui apparaît sur la figure une fois le point créé).
Utilisez l’icône ![]() pour créer une droite verticale passant par le point O. Pour utiliser cet outil il faut dérouler la deuxième barre d’icônes à partir du haut (par un double clic sur l’icône visible ou un clic sur la flèche jaune), cliquer sur l’icône
pour créer une droite verticale passant par le point O. Pour utiliser cet outil il faut dérouler la deuxième barre d’icônes à partir du haut (par un double clic sur l’icône visible ou un clic sur la flèche jaune), cliquer sur l’icône ![]() et cliquer sur le point O.
et cliquer sur le point O.
A l’aide de l’outil ![]() (première rangée d’icônes), créez un point lié à cette droite verticale que nous appellerons I.
(première rangée d’icônes), créez un point lié à cette droite verticale que nous appellerons I.
Utilisez l’icône ![]() pour créer le cercle de centre O et passant par I.
pour créer le cercle de centre O et passant par I.
Nous allons maintenant créer deux variables n et p.
La création des objets numériques se fait dans la troisième barres d’outils à partir du bas.
Utilisez l’icône ![]() et remplissez la boîte de dialogue comme ci-dessous (n’oubliez pas de cocher la case Dialogue associé) :
et remplissez la boîte de dialogue comme ci-dessous (n’oubliez pas de cocher la case Dialogue associé) :
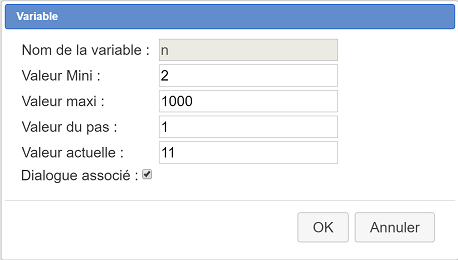
Vous remarquerez qu’une petite boîte de dialogue est apparue en bas et à droite de la fenêtre. Elle permet d’augmenter ou diminuer la variable n ou de la modifier.
Créez de même une variable p comme ci-dessous :
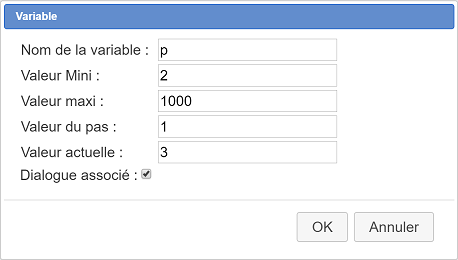
Nous allons maintenant créer une fonction f qui, à un entier x, associera l’angle de la rotation de centre O associant au point I le point représentant l’entier x sur notre cercle.
Utilisez pour cela l’icône ![]() située dans la troisième rangée d’icônes à partir du bas et remplissez la boîte de dialogue comme ci-dessous :
située dans la troisième rangée d’icônes à partir du bas et remplissez la boîte de dialogue comme ci-dessous :
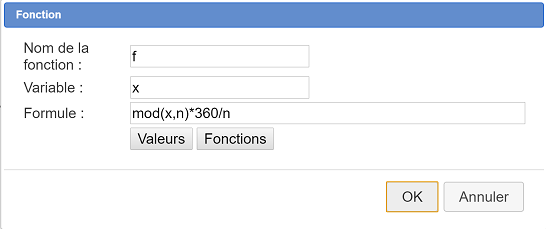
Voici la formule de la fonction : mod(x,n)*360/n
La fonction mod(x,n) renvoie le reste de la division euclidienne de x par l’entier n (x doit être un entier positif ou nul et n un entier strictement positif).
Nous devons maintenant créer des lieux d’objets dont le nombre d’objets sera la valeur de n. Une variable ne pouvant pas dépendre d’une autre variable, nous allons utiliser des lieux d’objets générés par un point lié.
Pour ce point lié nous utiliserons un curseur. Nous ne pouvons pas utiliser un curseur à valeurs entières car ce type de curseur ne peut pas générer de lieu.
Utilisez l’icône ![]() de création d’un curseur et choisissez un curseur de grande taille comme ci-dessous :
de création d’un curseur et choisissez un curseur de grande taille comme ci-dessous :
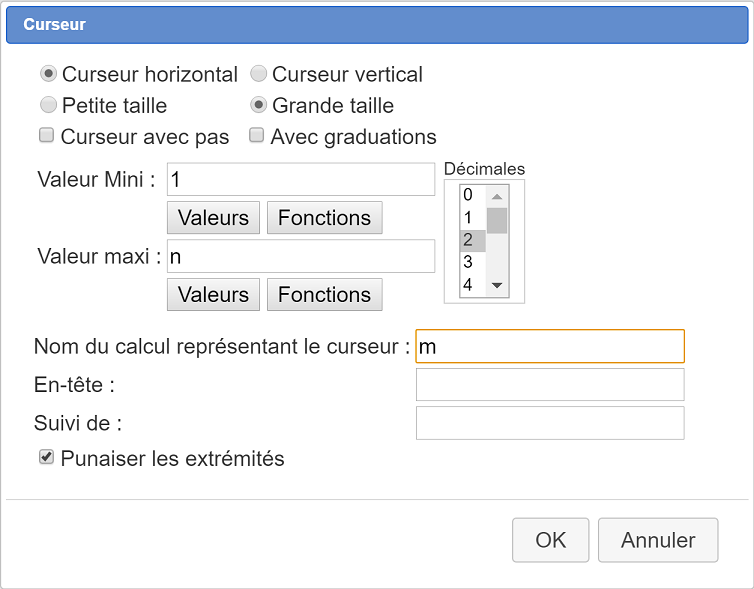
Les valeurs prises par notre curseur sont dans un calcul nommé m mais ce calcul ne prend pas de valeurs entières.
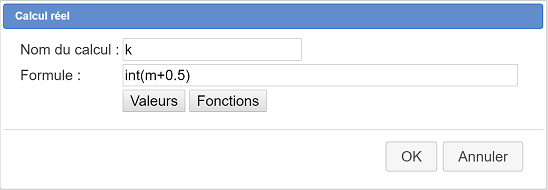
Nous allons donc utiliser l’icône ![]() pour créer un calcul nommé k qui prendra comme valeur l’entier le plus proche de m. Remplissez la boîte de dialogue comme ci-dessous :
pour créer un calcul nommé k qui prendra comme valeur l’entier le plus proche de m. Remplissez la boîte de dialogue comme ci-dessous :
Dans la palette de couleurs activez la couleur rouge.
Dans la barre d’icônes associée aux transformations (qui est par défaut celle de la translation) activez l’icône ![]() de la rotation.
de la rotation.
Cliquez sur le point O.
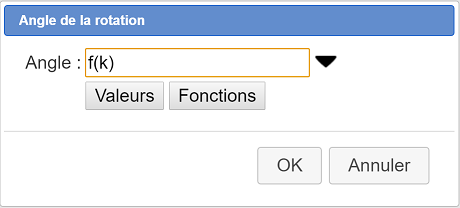
Une boîte de dialogue s’ouvre pour vous demander l’angle comme ci-dessous. Entrez comme angle f(k) comme ci-dessous :
Cliquez ensuite sur le point I pour créer son point image. Nommez ce point A.
Nous allons maintenant créer le point associé à l’entier $k \times p$
Cliquez à nouveau sur l’icône ![]() et cliquez sur le point O.
et cliquez sur le point O.
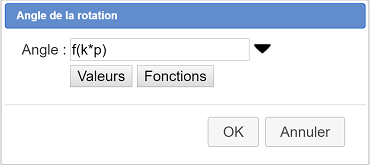
Cette fois entrez comme angle de la rotation f(k*p) comme ci-dessous :
Nommez ce point B.
Joignez les points A et B par un segment avec l’outil ![]()
En capturant avec l’outil ![]() le point mobile du curseur vous pouvez voir le segment [AB] varier.
le point mobile du curseur vous pouvez voir le segment [AB] varier.
Nous allons maintenant créer un lieu d’objet du point A généré par les positions du curseur.
Dans la palette de couleurs, activez la couleur bleue.
Pour cela utilisez l’icône ![]() de création d’un lieu d’objet généré par point lié.
de création d’un lieu d’objet généré par point lié.
Il vous est demandé de cliquer sur l’objet dont la trace génère le lieu : Cliquez sur le point A.
Il vous est ensuite demandé de cliquer sur le point lié dont les positions génèrent le lieu : Cliquez sur le point du curseur (qui clignote).
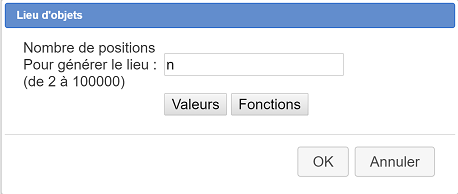
Une boîte de dialogue s’ouvre. Entrez n dans le champ Nombre de positions pour générer le lieu comme ci-dessous :
De même nous allons créer le lieu d’objet du segment généré par les positions du curseur.
Cliquez à nouveau sur l’icône ![]() , cliquez ensuite sur le segment [AB] puis sur le point du curseur qui clignote.
, cliquez ensuite sur le segment [AB] puis sur le point du curseur qui clignote.
Dans la boîte de dialogue qui s’ouvre, entrez n dans le champ Nombre de positions pour générer le lieu et validez.
A l’aide de l’icône ![]() , masquez les points A et B et le segment [AB] (en cliquant sur le segment il vous sera demandé si vous voulez désigner le segment ou le lieu d’objets).
, masquez les points A et B et le segment [AB] (en cliquant sur le segment il vous sera demandé si vous voulez désigner le segment ou le lieu d’objets).
Vous pouvez aussi masquer tous les éléments du curseur et la droite verticale passant par O..
Enregistrez votre figure avec l’outil ![]() de la barre d’outils supérieure.
de la barre d’outils supérieure.
Maintenant, en bas et à droite de la figure, cliquez sur le bouton = associé à la variable n. Dans le champ Valeur actuelle, entrez par exemple 399 et validez.
Ci-dessous la figure obtenue.
Vous pouvez maintenant cliquer sur les boutons + et - pour faire varier les valeurs de n et de p à votre guise.