Transformation barycentrique et utilisation de constructions.

Cet article a été révisé et adapté à la dernière version JavaScript de MathGraph32.

Nous allons ici illustrer un résultat que j’ai découvert et démontré il y a une quinzaine d’années. Ce résultat a été découvert en testant MathGraph32. C’est une conséquence du théorème de Ptolémée. Si vous êtes intéressés par la démonstration et des compléments vous les trouverez sur cette page.

Il s’agit ici de visualiser quelques propriétés de la transformation qui, étant donnés 3 points A, B et C, associe à tout point M le barycentre des points pondérés (A ; MA), (B ; MB) et (C ; MC).

Nous allons d’abord créer une construction qui créera l’image d’un point M par cette transformation.

Utilisez l’icône de la barre supérieure (nouvelle figure) et choisissez de créer une figure sans repère et avec longueur unité. Créez quatre points libres (icône ) et nommez-les A, B, C et M (icône ).

Utilisez l’outil pour mesurer les longueurs MA, MB et MC (vous pouvez vérifier après coup leur création en cliquant sur l’icône ).

Créons maintenant le barycentre à l’aide de l’outil . Pour cela, cliquez d’abord sur A. Une boîte de dialogue s’ouvre pour donner le coefficient. Utilisez le bouton Valeurs pour choisir comme coefficient MA puis validez (le coefficient choisi clignote au-dessous du point). Procédez de même pour affecter MB et MC comme coefficients respectifs à B et à C puis cliquez sur le bouton rouge en bas et à droite de la fenêtre pour créer le barycentre.

Nous pouvons maintenant créer notre construction.

Pour utiliser les constructions, cliquez dans la barre d’outils du haut sur l’icône qui fait apparaître des icônes supplémentaires.

Cliquez sur l’icône (création d’une construction) et choisissez l’item Choix des objets sources graphiques.

Cliquez sur A, B, C et M qui se mettent à clignoter puis cliquez en bas et à droite de la fenêtre sur le bouton rouge pour indiquer que vous avez fini de choisir les objets sources graphiques.

Cliquez de nouveau sur l’icône et choisissez l’item Choix des objets finaux graphiques.

Cliquez sur le barycentre que vous avez créé puis cliquez sur le bouton pour indiquer que vous avez fini de choisir les objets finaux graphiques.

Il nous reste à finaliser notre construction.

Cliquez de nouveau sur l’icône et choisissez l’item Finir la construction en cours et remplissez la boîte de dialogue comme ci-dessous :

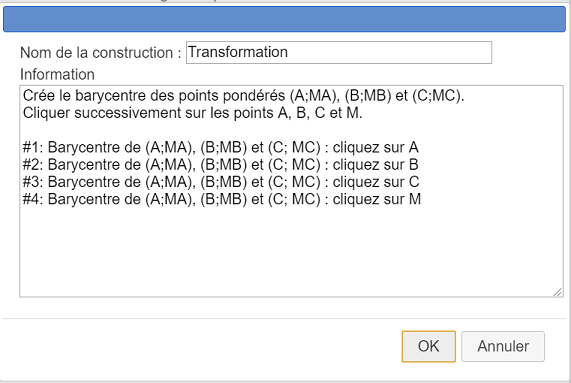
Voici ci-dessous le contenu du champ Information (les quatre dernières servent à afficher une indication pour le choix des 4 objets sources).

Notre construction fait partie de notre figure et sera enregistrée avec elle si vous l’enregistrez mais nous allons aussi l’enregistrer dans un fichier séparé.

Utilisez l’icône (gestion des constructions) et choisissez l’item Enregistrer une construction de la figure. Une boîte de dialogue s’ouvre vous présentant les constructions de la figure. La seule est notre construction Transformation et elle est déjà sélectionnée.

Cliquez sur le bouton Enregistrer pour enregistrer votre construction dans le dossier de votre choix à l’aide du menu (il est conseillé de garder le même nom pour le fichier de construction que pour la construction elle-même). Le fichier généré sera ainsi nommé Transformation.mgc.

Si nécessaire vous pouvez récupérer le ficher contenant cette construction dans le fichier zip ci-dessous :

Utilisez l’outil pour cacher le premier barycentre créé (l’objet final de notre première construction).

Créez maintenant deux points libres (icône ) et un cercle de centre le premier point et passant par le deuxième (icône ).

Créez un point lié à ce cercle (icône ) et nommez le N.

Cliquez de nouveau sur l’icône (gestion des constructions) et choisissez l’item Implementer une construction de la figure. Une boîte de dialogue s’ouvre. La seule construction présente Transformation est déjà sélectionnée.
Validez par OK.

Un affichage fugitif en haut et à droite de la figure affiche : Barycentre de (A ;MA), (B ;MB) et (C ; MC) : cliquez sur A. Cliquez donc sur le point A.

Cliquez ensuite sur B, sur C puis sur le point N (qui jouera le rôle du point M initial de notre construction).

Un nouveau point apparaît qui a été créé par notre construction. Si vous capturez le point N vous voyez ce nouveau point se déplacer (c’est le barycentre des points pondérés (A ;NA), (B ;NB) et (C ; NC)).

Dans la palette de couleurs activez par exemple la couleur bleue.

Nous allons créer le lieu de ce nouveau point généré par le déplacement du point N sur le cercle.

Utilisez pour cela l’icône (lieu de points généré par point lié).

Cliquez d’abord sur le point créé par la construction (point dont les traces généreront le lieu) puis sur le point N (point lié dont les positions généreront le lieu de points). Une boîte de dialogue s’ouvre. Demandez 400 points et cochez la case Lieu fermé. Validez.

Voici ci-dessous un exemple de figure obtenue :

Nous allons maintenant créer une nouvelle macro-construction qui, à partir des points A, B et C et du cercle construira comme objet final le lieu de points que nous venons de créer.

Utilisez l’icône (création d’une construction) et choisissez l’item Choix des objets sources graphiques.

Cliquez successivement sur A, B et C puis sur le cercle. Cliquez ensuite sur le bouton .

Utilisez à nouveau l’icône et choisissez l’item Choix des objets finaux graphiques.

Cliquez sur le lieu de points que vous venez de créer puis cliquez sur le bouton .

Il reste à finaliser la construction. Cliquez à nouveau sur l"icône et choisissez l’item Finir la construction en cours.

Remplissez la boîte de dialogue comme ci-dessous.

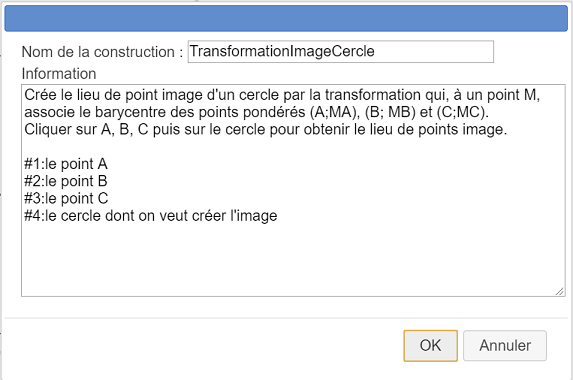
Voici ci-dessous le contenu à entrer dans le champ Information :

Enregistrons maintenant cette construction dans un fichier séparé.

Utilisez l’icône (gestion des constructions) et choisissez l’item Enregistrer une construction de la figure.

Cette fois sélectionnez dans la liste la construction nommé TransformationImageCercle et cliquez sur le bouton Enregistrer pour enregistrer cette construction dans le même dossier que la construction précédente (le fichier créé sera TransformationImageCercle .mgc).

Vous pouvez éventuellement télécharger cette construction dans le fichier zip ci-dessous.

Nous allons maintenant utiliser cette dernière construction dans une autre figure.

Par précaution enregistrez d’abord la figure actuelle puis utilisez l’icône pour créer une nouvelle figure avec longueur unité mais sans repère.

Créez deux points libres (icône ) et un cercle de centre le premier point et passant par le second (icône ). Nommez O le centre (icône ).

Avec l’outil créez trois points liés à ce cercle et nommez-les A, B et C. Joignez ces trois points par trois segments (outil ).

Utilisez l’icône (gestion des constructions) et choisissez l’item Incorporer une construction depuis un fichier et allez chercher la construction nommée TransformationImageCercle dans le répertoire où vous l’avez enregistrée.

Utilisez à nouveau l’icône et choisissez l’item Implémenter une construction de la figure. Notre unique construction TransformationImageCercle est déjà sélectionnée. Cliquez sur bouton Implémenter.

Cliquez d’abord sur les points A, B et C puis sur le cercle.

Le lieu image apparaît. Vous constatez qu’il semble s’agir d’un triangle dont les sommets sont sur les côtés du triangle ABC.

Utiliser l’icône pour créer un point lié au cercle. Nommez ce point M.

Nous allons aussi créer l’image de ce point M par la transformation.

Utilisez l’icône (gestion des constructions) et choisissez l’item Incorporer une construction depuis un fichier et allez cherche la construction nommée Transformation dans le répertoire où vous l’avez enregistrée.

Utilisez à nouveau l’icône et choisissez l’item Implémenter une construction de la figure.

Dans la liste proposée, cliquez sur la construction nommée Transformation et cliquez sur le bouton Implémenter.

Cliquez dans cet ordre sur A, B, C puis M. 

Le point image par la transformation apparaît. Il est bien sûr sur notre lieu de point créé par la précédente transformation. Nommez-le G.

Voici la figure obtenue :

Capturez le point M et observez le déplacement du point G sur le lieu de point image.

Nous allons maintenant illustrer l’image par cette transformation de l’intérieur du cercle circonscrit au triangle ABC.

Créez le segment [OA] (icône ) et un point lié à ce segment que nous appellerons P (outil ).

Créez maintenant le cercle de centre O et passant par P (icône ).

Utilisez à nouveau l’icône et choisissez l’item Implémenter une construction de la figure.

Cette fois sélectionnez la macro-construction TransformationImagCercle et cliquez sur le bouton Implémenter.

Cliquez sur les points A, B et C puis sur le cercle de centre O et passant par P. Le lieu de points image de ce cercle apparaît comme sur la figure ci-dessous :

Nous allons maintenant créer le lieu d’objets de ce lieu de points qui sera généré par les positions de P sur le segment [OA].

Dans la palette des couleurs, activez la couleur rouge.

Déroulez la barre d’outils des lieux et cliquez sur l’icône (lieu d’objets généré par point lié).

On vous demande d’abord de cliquer sur l’objet dont la trace générera le lieu : cliquez sur le dernier lieu de points (celui créé par la macro construction).

On vous demande ensuite de cliquer sur le point lié dont les positions généreront le lieu : cliquez sur sur le point P.

Dans la boîte de dialogue qui apparaît demandez par exemple 30 objets.

Voici donc la figure finale obtenue :

Notons que vous pouvez changer la couleur du lieu d’objet avec l’outil mais pas son style de trait qui reste celui du lieu de points avec lequel il est généré.

Capturez le point P. Cette figure semble suggérer le résultat suivant : l’image par la transformation de l’intérieur du cercle circonscrit un triangle ABC est l’intérieur du triangle image de ce cercle par la transformation.

Capturez aussi les points A, B et C.