Toutes les versions de cet article : [English] [Español] [français]
Créez une nouvelle figure avec Utilisez l’icône ![]() de la barre supérieure et choisir un repère othonormal avec pointillés.
de la barre supérieure et choisir un repère othonormal avec pointillés.
Créez six points de coordonnées respectives (-2 ;0), (-1 ;1), (0 ;0), (1 ;-1), (2 ;0) et (4 ;2) (outil ![]() ).
).
Créez six calculs numériques nommés m1, m2, ..., m6 et contenant comme formules respectivement 2, 0, -2, 0, 2 et 2 (outil ![]() ).
).
Nous allons maintenant utiliser une construction fournie avec MathGraph32 Java (version 3.3.0 ou ultérieure) permettant de créer une courbe de fonction dérivable passant par six points donnés connaissant les coefficients directeurs des tangentes en ces six points.
Utilisez pour cela menu Constructions - Implémenter une construction prédéfinie. Une boîte de dialogue s’ouvre. Ouvrez le dossier nommé Courbes avec tangentes et ouvrez la construction nommée CourbePar6PointsAvecCoeffDirTang.
Une boîte de dialogue s’ouvre pour choisir les élements sources non graphiques qui sont les coefficients directeurs des tangentes. Affectez aux 6 premiers éléments respectivement les calculs m1, m2, m3, m4, m5 et m6, et affectez au septième élément le repère (O,I,J) et validez.
Vous devez ensuite cliquer sur les points créés en les désignant par ordre d’abscisses croissantes.
La courbe apparaît. En appuyant sur la touche F6 vous verrez que dans les objets finaux figurent une fonction nommée f et de mesures de coordonnées de ces points.
Activez la couleur bleue et le style de trait pointillé.
Créez maintenant un point lié à l’axe des ordonnées (![]() ) et nommez-le k (icône
) et nommez-le k (icône ![]() ).
).
Mesurez l’ordonnée du point k dans le repère avec l’icône (![]() . Cette ordonnée est notée yCoord(k,O,I,J).
. Cette ordonnée est notée yCoord(k,O,I,J).
Créez un calcul nommé k contenant comme formule yCoord(k,O,I,J) (outil ![]() , utilisez le bouton Liste des valeurs).
, utilisez le bouton Liste des valeurs).
Créez la parallèle à l’axe des abscisses passant par k (icône ![]() ).
).
Créons une nouvelle fonction nommée g définie par g(t)=f(t)-k (menu Calculs >> Nouveau calcul dans R >> Fonction réelle).
Amenez si nécessaire le point k à une position telle que son ordonnée soit comprise entre 0 et 1.
Utilisez le menu Calculs >> Nouveau calcul dans R >> Solution approchée d’équation f(x)=0 et remplissez la boîte de dialogue comme ci-dessous.
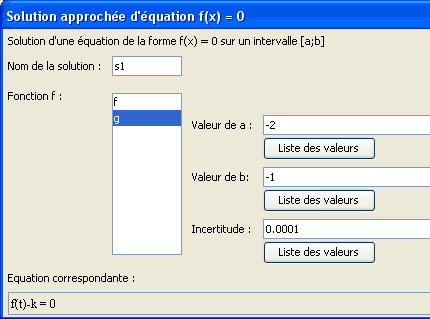
Appuyez sur F9 pour utiliser à nouveau ce dernier outil et complétez la boîte de dialogue comme ci-dessous.
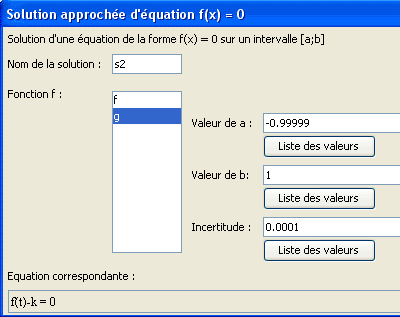
Procédez de même comme ci-dessous :
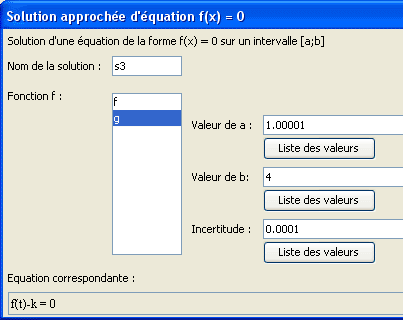
Créez maintenant 3 calculs nommés ys1, ys2 et ys3 contenant comme formules f(s1), f(s2) et f(s3) (outil ![]() ).
).
Nous allons maintenant visualiser les solutions (quand elles existent).
Activez la couleur rouge.
Créez les points de coordonnées (s1 ; 0), (s2 ;0) et (s3 ; 0) (icône ![]() ).
).
Créons un affichage de la valeur de s1 lié au point de coordonnées (s1 ;0) à l’aide de l’icône ![]() . Cliquez sur le point et remplissez la boîte de dialogue comme ci-dessous.
. Cliquez sur le point et remplissez la boîte de dialogue comme ci-dessous.
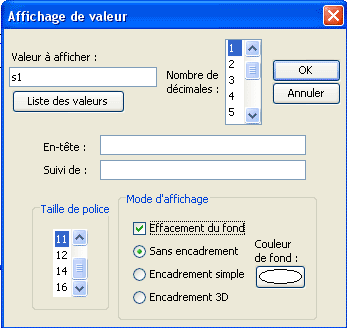
Créez de même un affichage de la valeur de s2 lié au point de coordonnées (s2 ;0) et un affichage de s3 lié au point de coordonnées (s3 ;0).
Nous cherchons maintenant à calculer et afficher le nombre de solutions de l’équation f(x)=k.
Nous allons d’abord créer trois tests d’existence.
Utilisez le menu Calculs >> Nouveau calcul dans R >> Test d’existence d’une valeur. Remplissez la boîte de dialogue ci-dessous.
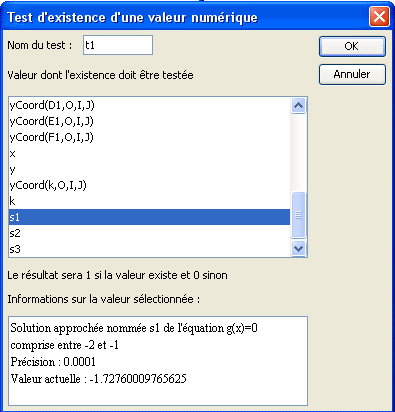
Le test t1 rendra comme valeur 1 quand s1 existe et 0 sinon.
Procédez de même pour créer des tests d’existence de s2 et s3 nommés t2 et t3.
Créez maintenant un calcul nommé N comme ci-dessous (outil ![]() ).
).
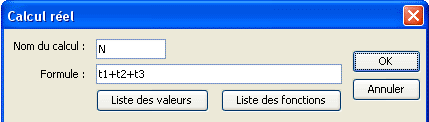
Le calcul N contient maintenant le nombre de solutions de l’équation f(x)=k.
Nous allons maintenant utiliser une possibilité avancée de MathGraph32 qui est la possibilité d’insérer dans un commentaire des affichages de valeurs dynamiques.
Utilisez l’outil ![]() . Cliquez en haut et à gauche de la figure.
. Cliquez en haut et à gauche de la figure.
Commencez par remplir la boîte de dialogue comme ci-dessous.
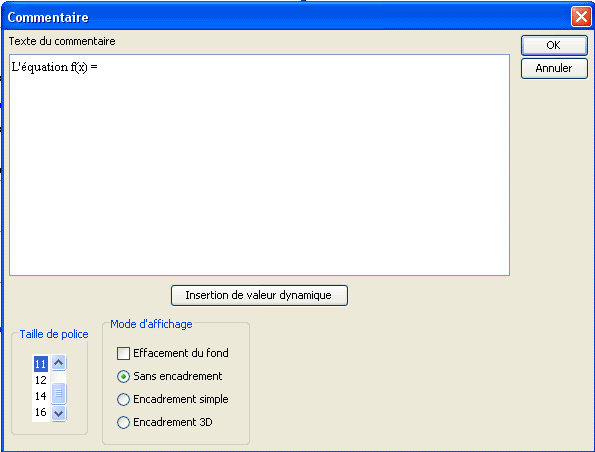
Cliquez sur le bouton Insertion d’affichage dynamique.
Remplissez la nouvelle boîte de dialogue comme ci-dessous et validez.
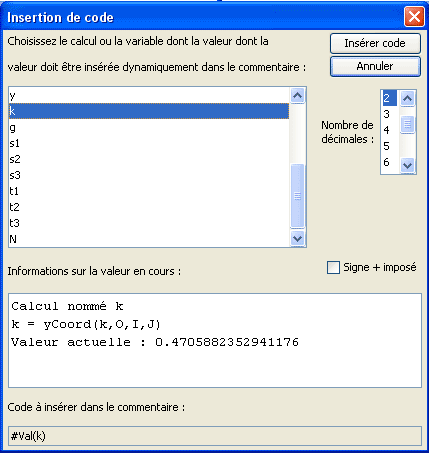
Complétez le texte comme ci-dessous puis cliquez à nouveau sur le bouton Insertion d’affichage dynamique.
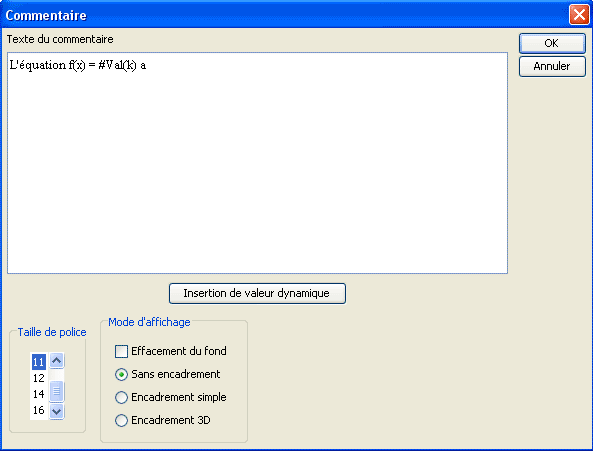
Remplissez la nouvelle boîte de dialogue comme ci-dessous et validez.
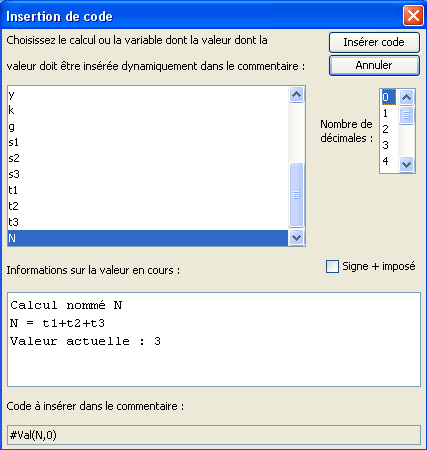
Finissez de remplir la boîte de dialogue comme ci-dessous :
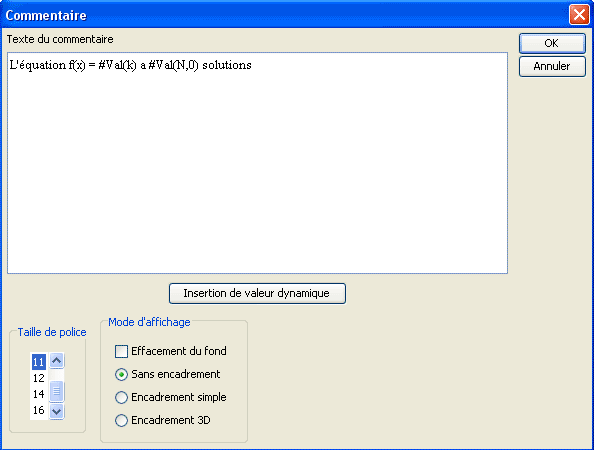
Validez.
Capturez maintenant le point k pour visualiser les solutions de l’équation f(x)=k et leur nombre.
Voici la figure ci-dessous animée par le moteur JavaScript de MathGraph32 :