Toutes les versions de cet article : [English] [Español] [français]
Crea una nueva figura con el menú Archivo >> Nueva figura con >> Referencial ortonormal >> Punteado.
Crea una nueva figura con el menú Archivo >> Nueva figura con >> Referencial ortonormal >> Punteado.
Crea seis puntos de coordenadas respectivas (–2 ;0), (–1 ;1), (0 ;0), (1 ; –1), (2 ;0) y (4 ;2) (herramienta ![]() ).
).
Crea seis cálculos numéricoss nominados m1, m2, ..., m6 y que contengan como fórmula respectivamente 2, 0, –2, 0, 2 y 2 (herramienta ![]() ).
).
Vamos ahora a utilizar una construcción proporcionada con la versión 2.5 de MathGraph32 que permite crear una curva de función derivable que pasa por seis puntos dados conociendo los coeficientes directores de las tangentes en estos seis puntos.
Deben antes tener cargado las construcciones proporcionadas con la versión Java. Si no es el caso, pulsan aquí, descomprimen el archivo zipeado en un lugar de vuestra elección.
Se aconseja utilizar el menú Opciones >> Preferencias, pestaña Directorio de construcciones para que MathGraph32 vaya a buscar cada vez en la carpeta donde pusieron sus construcciones favoritas
Utiliza para ello el menú Construcción >> Implementar una construcción desde un archivo. Una caja de diálogo se abre. Abre la carpeta llamada Courbes avec tangentes y abre la construcción llamada CourbePar6PointsAvecCoeffDirTang.
Una caja de diálogo se abre para elegir los elementos fuentes non gráficos que son los coeficientes directores de las tangentes. Afecta a los 6 primeros elementos respectivamente los cálculos m1, m2, m3, m4, m5 y m6, y afeca al séptimo elemento el referencial (O,I,J) y valida.
A continuación cliquea sobre los puntos creados designándolos por orden de abscisas crecientes.
La curva aparece. Al apretar la tecla F6 verás que en los objetos finales figura una función nombrada f y las medidas de coordenadas de estos puntos. También aparece un punto M sobre la curva, punto que es móvil capturando el punto nombrado x.
Activa el color azul y el estilo de trazo punteado.
Crea ahora un punto ligado al eje de las ordenadas (![]() ) y nómbralo k (icône
) y nómbralo k (icône ![]() ).
).
Mide la ordenada del punto k en el referencial con el icono (![]() . Esta ordenada es denotada por Coord(k,O,I,J).
. Esta ordenada es denotada por Coord(k,O,I,J).
Crea un cálculo nombrado k que contiene como fórmula yCoord (k, O, I, J) (herramienta ![]() , utiliza el botón Lista de los valores).
, utiliza el botón Lista de los valores).
Crea la paralela al eje de las abscisas que pasa por k (ícono ![]() ).
).
Creemos una nueva función nombrada g definida por g (t) =f (t) – k (menú Cálculos >> Nuevo cálculo en R >> Función real).
Mueve, en caso de ser necesario, el punto k a una posición tal que su ordenada esté incluida entre 0 y 1.
Utiliza el menú Cálculos >> Nuevo cálculo en R >> Solución aproximada de ecuación f (x) =0 y completa la caja de diálogo como abajo.
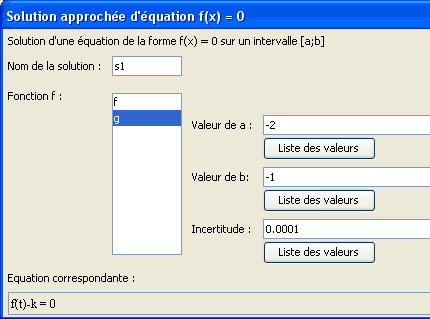
Oprime la tecla F9 para utilizar de nuevo esta última herramienta y completa la caja de diálogo como abajo.
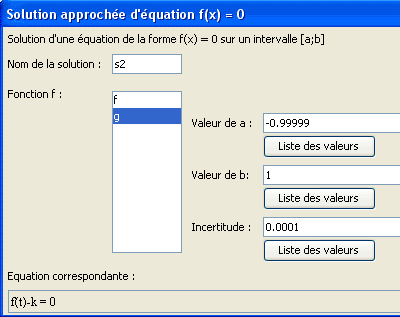
Procede asimismo como abajo :
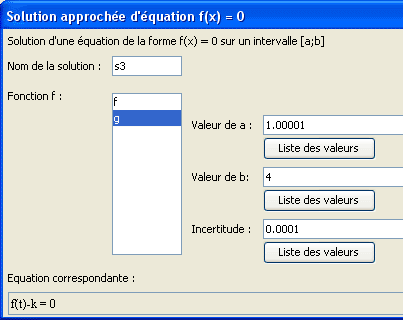
Crea ahora 3 cálculos nombrados ys1, ys2 y ys3 conteniendo como fórmulas f (s1), f (s2) y f (s3) (herramienta ![]() ).
).
Vamos ahora a visualizar las soluciones (cuando ellas existen)
Activa el color rojo.
Creemos una visualización del valor de s1 vinculada al punto de coordenadas (s1 ; 0) con ayuda del menú Crear >> Visualización de valor >> Ligado a un punto. Cliquea sobre el punto y llena la caja de diálogo como abajo.
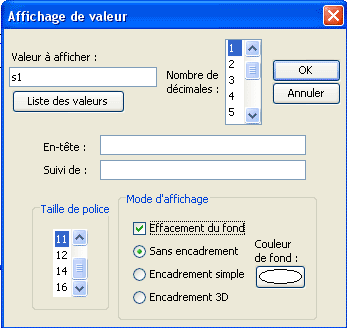
Crea análogamente una visualización del valor de s2 ligada al punto de coordenadas (s2 ; 0) y una visualización de s3 ligada al punto de coordenadas (s3 ; 0).
Buscamos ahora a calcular e indicar el número de soluciones de la ecuación f (x) =k.
Vamos en primer lugar a crear tres tests de existencia.
Utiliza el menú Cálculos >> Nuevo cálculo en R >> Prueba de existencia de un valor. Llena la caja de diálogo siguiente.
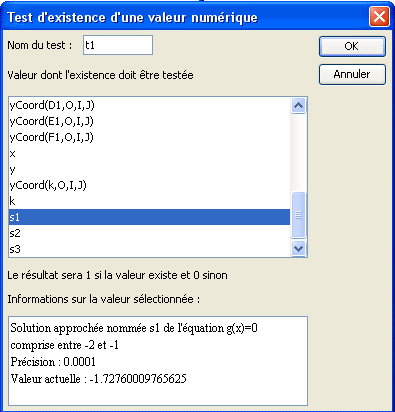
El test t1 devolverá como valor 1 cuando s1 existe y 0 si no.
Procede de la misma manera para crear tests de existencia de s2 y s3 nombrados t2 y t3.
Crea ahora un cálculo nombrado N como abajo (outil ![]() ).
).
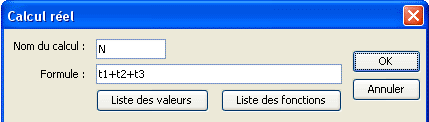
El cálculo N contiene ahora el número de soluciones de la ecuación f (x) =k.
Vamos ahora a utilizar una posibilidad avanzada de MathGraph32 que es la posibilidad de insertar en un comentario visualizaciones de valores dinámicas.
Utiliza la herramienta![]() . Cliquea arriba y a la izquierda de la figura.
. Cliquea arriba y a la izquierda de la figura.
Comienza por llenar la caja de diálogo como abajo.
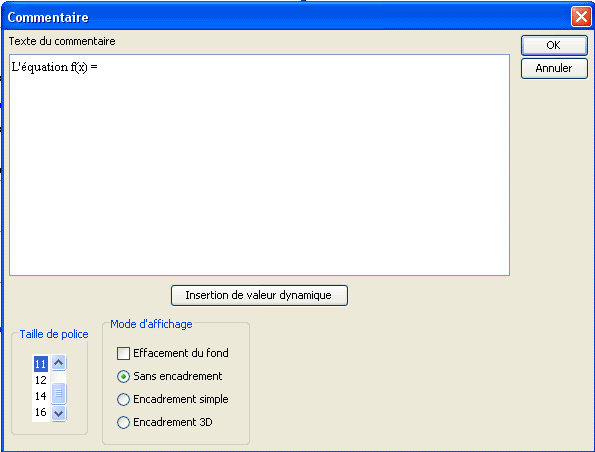
Cliquea sobre el botón Inserción de visualización dinámica
Llena la nueva caja de diálogo como abajo y valida.
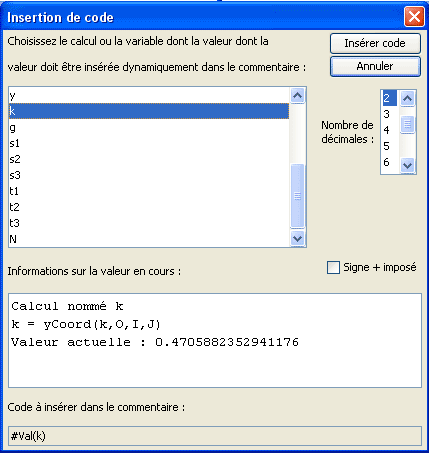
Completa el texto como abajo luego cliquea de nuevo sobre el botón Inserción de visualización dinámica.
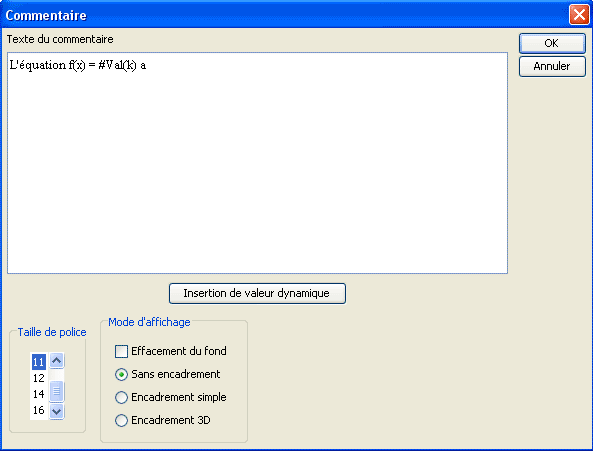
Llena la nueva caja de diálogo como abajo y valida.
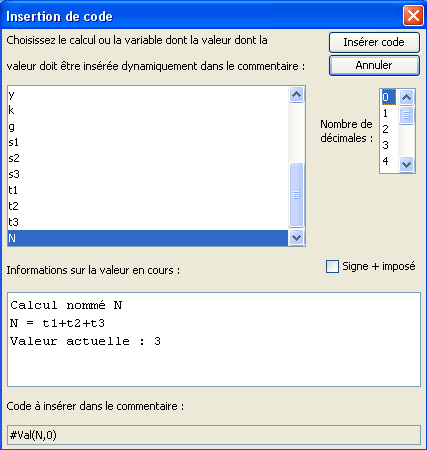
Termina de llenar la caja de diálogo como abajo :
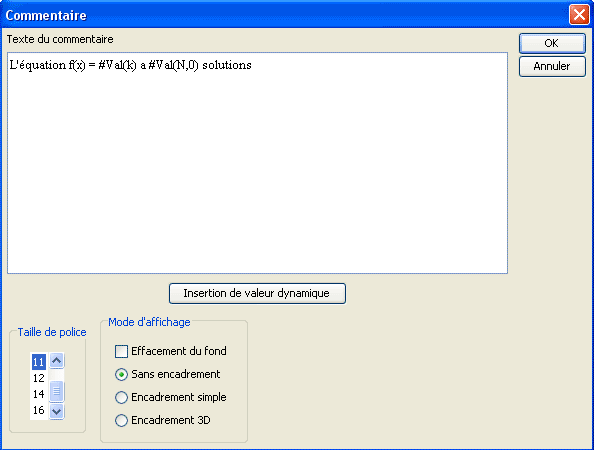
Valida.
Captura ahora el punto k para visualizar las soluciones de la ecuación f (x) =k y su número.
Se obtiene así la figura de abajo animada por el JavaScript motor de MathGraph32 :