La suite récurrente réelle
Il s'agit d'une suite définie par une formule d'un des trois types suivants :
u(n+1) = f[u(n)] où f désigne une fonction réelle d'une variable réelle.
u(n+1)=f[n,u(n)] où f désigne une fonction réelle de deux variables réelles.
u(n+2)=f[n,u(n+1),u(n)] où f désigne une fonction réelle de trois variables réelles.
On crée une somme indicée en utilisant l'icône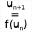 
de la troisième rangée d'icônes à partir du bas.
Une boîte de dialogue s'ouvre.
Il vous est demandé :
Les indices de la suite commencent à zéro.
Une fois la suite créée, vous pouvez par la suite utiliser un des termes de cette suite avec la syntaxe suivante : Si la suite s'appelle u, u(indice) renverra le terme de la suite d'indice indice. Ce terme n'existe que si indice est entier et strictement inférieur au nombre de termes de la suite (sous réserve d'existence de ce terme).
Voir aussi : Le graphe de suite récurrente.