High school level example 2 (Java version) : Illustration of a property of integrals

We want to creat the figure below (animated through MathGraph32 applet).

You can capture a and b.

Make sure that MathGraph32 uses radian as angle unity (menu item Options - Preférences, Angle unity tab.

Crate a new figure with a frame (for example with menu item File - New figure with - Frame without vectors).

Use icon to create a real function named f defined by f(t)=sin(pi*t)^2+cos(pi*t)+1 as shown below :

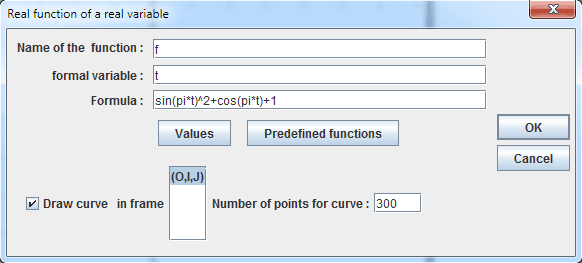
Set the checkbox DrawCurve selected so that the curve of the function will be created.

You can use icon (keyboard shortcut F5) to see how MathGraph32 creates a function curve.

In the color palette, activate the blue color.

Use tool to create a point linked to the x-axis and name this point a.

Use tool to measure the abscissa of point a in frame (O,I,J). Un message pops up warning you that this measure is represented as xCoord(a,O,I,J)).

Now use tool to create a calculus named a with formula xCoord(a,O,I,J) (use button Values).

So a contains now the abscissa of point a.

Create point of coordinates (a + 2 ; 0) (tool ).

We will now create a text display linked to point a.

For this, use tool .

Click on point a. A dialog box pops up. Enter a + 2 in the text field and validate. This linked point will move with point a. You can use tool to change the position of the text relativaly to point a.

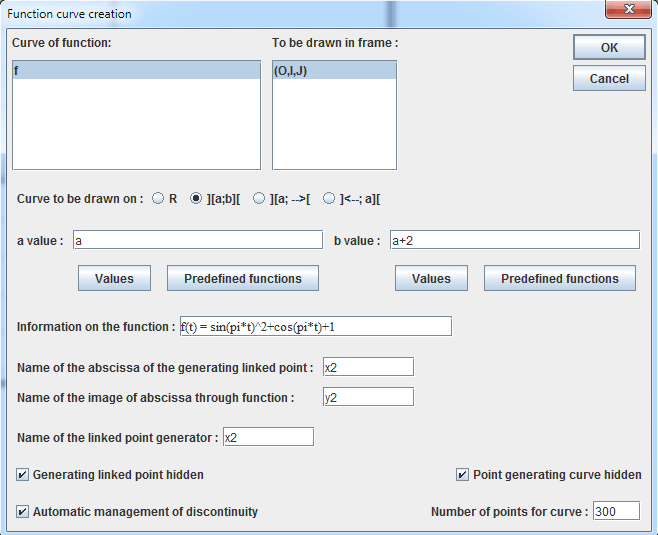
Let’s now create the curve of function f on [a ; a + 2] interval with tool .

In the dialog box popping up, set checked the item Curve to be drawn on ][a ;b][. Fill it as shown below :

In the filling style palette, click on . Then use icon to fill the surface between this last curve and the x-axis (click first on the curve which is a point locus and then on the x-axis). When asked for the first or last object for the point locus, choose last object.

Now create points with coordinates (a ; f(a)) and (a + 2 ; f(a + 2)) (tool ) and then join with dotted segments points of coordinates (a ; 0) to (a ; f(a)) and (a + 2 ; 0) to (a + 2 ; f(a + 2)) (tool ).

Now mask the last curve (tool ). It is the last object.

In the color palette, click on green color.

Create now a point linked to the x-axis which you will name b (tool ) and measure the abscissa of b (tool ).

Create a new calculus named b containing this abscissa ant then the curve of function f on interval [b ; b + 2] (tool ).

In the filling style palette, click on style .

Click on icon for a personalized color choice. A dialog box pops up. Choose a light green color and validate.

Just as before, create the surface between the curve of f on interval [b ; b + 2] and the x-axis.

Let’s get our figure improved to illustrate the fact taht our function f is perdiodical of period 2.

In the color palette, activate the black color and in the line style palette activate the thick continuous line.

Click on tool of vector creation. Click then on points of coordinates (a ; f(a)) et (a + 2 ; f(a + 2)).

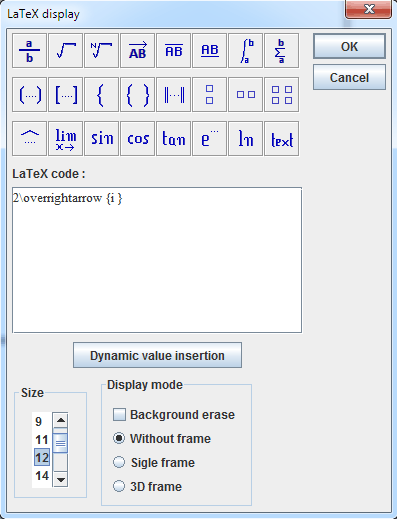
Let’s create now a special LaTeX display, this one will be linked to the point of coordinates (a + 2 ; f(a + 2)). It will display $2\overrightarrow{i}$

In the dialog box that pops up, enter 2 in the text editor then click on icon . In the LaTexCode adden, enter i between the brackets and validate just as below :

You can now use tool
to change the position of the LaTeX display relatively the the point.