Toutes les versions de cet article : [Español] [français]
Depuis la version 3.5, MathGraph32 possède des fonctions LaTeX spéciales avancées que nous allons illustrer dans cet exemple.
Nous désirons tracer la courbe représentative d’une fonction polynôme de de degré inférieur ou égal à 2 et une tangente à la courbe.
Pour cela, créons une nouvelle figure munie d’un repère avec l’icône ![]() de la barre supérieure et choisissons un repère orthonormal.
de la barre supérieure et choisissons un repère orthonormal.
Créons en haut et à gauche de la figure un premier curseur à valeurs entières qui fera varier les valeurs de a. Pour cela, cliquez sur l’icône ![]() puis cliquez en haut et à gauche de la figure.
puis cliquez en haut et à gauche de la figure.
Remplissez la boîte de dialogue comme ci-dessous puis validez (n’oubliez pas de cocher la case Curseur à valeurs entières).
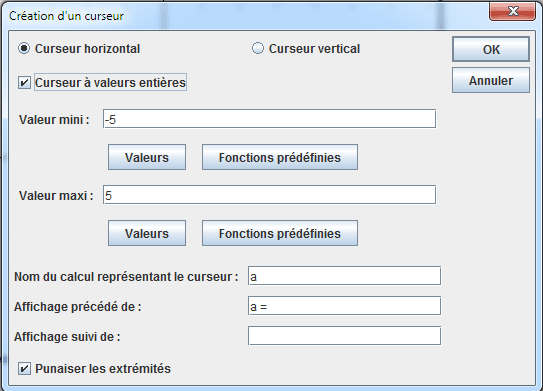
De même créez en dessous du curseur deux nouveaux curseurs à valeurs entières qui feront varier les valeurs de b et c.
A noter : Les extrémités gauches et droites du curseur sont punaisées par défaut. Si vous désirez déplacer le curseur, commencez par dépunaiser l’extrémité gauche avec l’outil ![]() puis capturez l’extrémité gauche avec l’outil de capture
puis capturez l’extrémité gauche avec l’outil de capture ![]()
Dans la palette de couleur, activez la couleur bleue.
Utilisons maintenant l’icône ![]() pour créer la fonction et obtenir sa courbe.
pour créer la fonction et obtenir sa courbe.
Remplissez la boîte de dialogue comme ci-dessous et validez.
La courbe de la fonction apparaît en bleu.
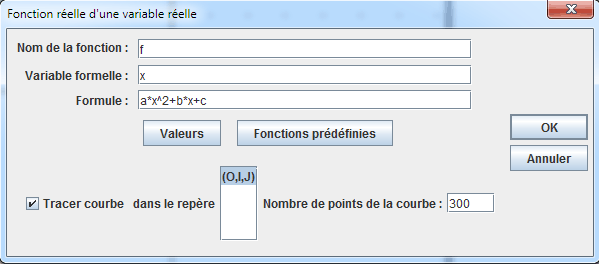
Pour écrire sur la figure la formule de f(x) sous la forme la plus simple possible, nous allons utiliser un affichage LaTeX.
Dans la palette de couleurs, activez la couleur bleue.
Cliquez sur l’icône ![]() puis cliquez en haut et à droite de la figure.
puis cliquez en haut et à droite de la figure.
Dans la boîte de dialogue qui s’ouvre, entrez le code LaTeX suivant : f(x)=\ForSimp{f} et validez.
La fonction LaTeX \ForSimp est spécifique à MathGraph32 : les valeurs de a, b et c ont remplacées puis l’affichage de la formule écrit sous la forme la plus simple possible.
L’affichage de la formule apparait en haut et à droite de la figure.
Dans la palette de couleurs, activez la couleur rouge et à l’aide de l’icône ![]() créez un point lié à la courbe (la courbe est en fait un lieu de points). Utilisez l’icône
créez un point lié à la courbe (la courbe est en fait un lieu de points). Utilisez l’icône ![]() pour nommer ce point M.
pour nommer ce point M.
Mesurez maintenant l’abscisse de M dans le repère avec l’outil ![]() .
.
Nous allons maintenant demander à MathGraph32 de créer la tangente à la courbe de la fonction f au point M. Pour cela utilisons l’outil ![]() . Une boîte de dialogue s’ouvre. Remplissez-la comme ci-dessous.
. Une boîte de dialogue s’ouvre. Remplissez-la comme ci-dessous.
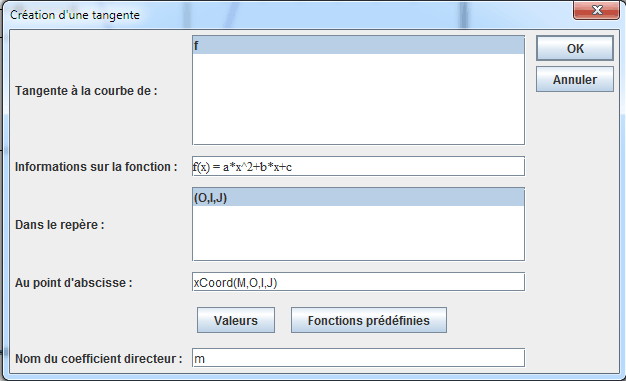
La tangente en M apparaît. Il faut remarquer qu’il s’agit d’une vraie tangente issue d’un calcul interne d’une dérivée formelle.
Demandons maintenant à MathGraph32 d’afficher l’équation réduite de cette tangente. Cliquez sur l’icône ![]() . Il vous est demandé dans la ligne d’indication de cliquer à l’endroit où sera affichée cette équation. Cliquez au-dessous du dernier curseur puis renseignez la boîte de dialogue comme ci-dessous :
. Il vous est demandé dans la ligne d’indication de cliquer à l’endroit où sera affichée cette équation. Cliquez au-dessous du dernier curseur puis renseignez la boîte de dialogue comme ci-dessous :
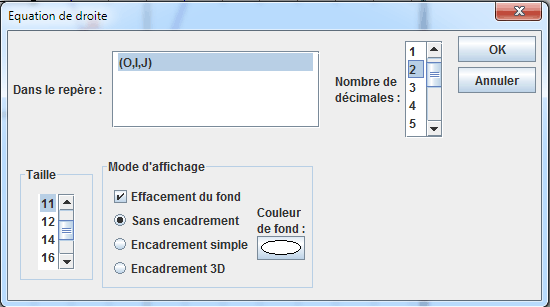
Vous pouvez maintenant capturer M et faire varier les valeurs de a, b et c. Vous remarquerez que la formule de la fonction est toujours écrite sous la forme la plus simple possible.
Voici ci-dessous la figure obtenue :