Toutes les versions de cet article : [Español] [français]
Nous montrerons dans cet article comment utiliser en classe une figure pour illustrer un problème d’optimisation linéaire. Il est conseillé d’utiliser pour cela la version 4.2.1 de MathGraph32 Java (ou ultérieure).
Nous voulons illustrer l’exercice suivant :
Un vendeur ambulant propose deux catégories de hamburgers :
– Le " simple" : 3 min de préparation, 50 g de garniture, 0,8 € de bénéfice.
– Le " maxi" : 5 min de préparation, 150 g de garniture, 1 € de bénéfice.
Pour cela, il dispose de 9 kg de garniture et ne peut consacrer que six heures par jour à leur préparation.
Il sait qu’il ne peut pas espérer vendre plus de 100 hamburgers par jour.
1) Calculer le temps de préparation et la garniture nécessaire à la fabrication de 50 "simples" et 30 "maxis".
Calculer le bénéfice réalisé.
2) On appelle x le nombre de hamburgers "simples" et y le nombre de "maxis" fabriqués par jour (x et y entiers positifs).
Écrire sous forme d’inégalités les contraintes qui portent sur x et y.
Représenter graphiquement les points M (x ; y) du plan satisfaisant à ces contraintes.
3) Écrire à l’aide de x et y le bénéfice réalisé B (en €).
4) Pour chaque réel B, on appelle $\Delta_B$ la droite d’équation 0,8x+y = B.
Tracer la droite $\Delta_{70}$ .
5) Quel nombre de hamburgers de chaque type doit-il préparer pour que son bénéfice soit maximum ?
Depuis la version 4.2 de MathGraph32 il est possible de travailler dans un (ou plusieurs) repère en spécifiant une unité sur chaque axe.
Commençons par créer une figure avec un repère à l’aide de l’icône ![]() de la barre supérieure. Remplir la boîte de dialogue qui s’ouvre comme ci-dessous.
de la barre supérieure. Remplir la boîte de dialogue qui s’ouvre comme ci-dessous.
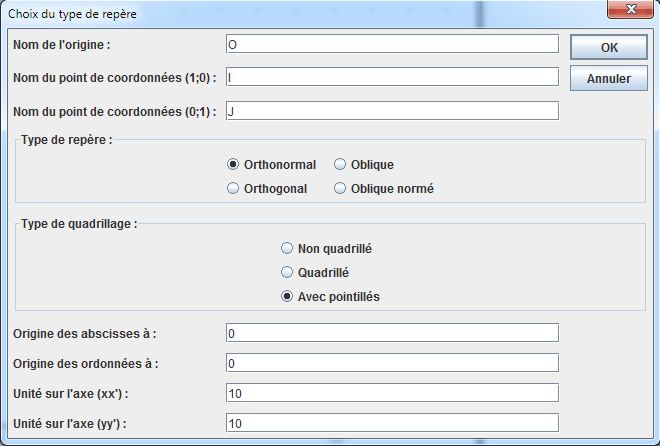
Agrandissez un peu en hauteur la fenêtre de cette nouvelle figure et utilisez l’outil de capture ![]() pour amener l’origine O en bas et à gauche de la figure et rapprochez un peu le point I du point O.
pour amener l’origine O en bas et à gauche de la figure et rapprochez un peu le point I du point O.
Pour plus de lisibilité nous allons cacher les noms des points I et J. Pour cela activez l’outil ![]() et cliquez sur le point puis cochez la case Nom masqué.
et cliquez sur le point puis cochez la case Nom masqué.
A l’aide de l’icône ![]() (raccourci clavier Ctrl + Ins) créez les points de coordonnées (100 ;0) et (0 ;100).
(raccourci clavier Ctrl + Ins) créez les points de coordonnées (100 ;0) et (0 ;100).
Cliquez sur l’outil ![]() de création d’un affichage LaTeX lié à un point puis cliquez sur le point I (dont le nom est masqué). Entrez 100 dans le champ Code LaTeX et validez.
de création d’un affichage LaTeX lié à un point puis cliquez sur le point I (dont le nom est masqué). Entrez 100 dans le champ Code LaTeX et validez.
Procédez de même avec le point J.
Rappelons que si on veut modifier un objet graphique créé par une boîte de dialogue comme nos affichages LaTeX il suffit d’utiliser l’outil ![]() et de cliquer sur l’objet.
et de cliquer sur l’objet.
Les contraintes sur x et y sont les suivantes :
– $x\ge0$
– $y\ge0$
– $3x + 5y\le360$
– $50x +150y\le9000$
– $x+y\le100$
Nous allons les représenter graphiquement.
Commençons par créer la droite d’équation $3x + 5y = 360$.
Pour cela il suffit de cliquer sur l’icône ![]() de création d’une droite par une équation.
de création d’une droite par une équation.
Dans la boîte de dialogue qui s’ouvre, entrez 3*x+5*y = 360 dans le champ Equation. Utilisez ensuite l’icône ![]() pour nommer cette droite D1.
pour nommer cette droite D1.
Créez de même les droites d’équations $50x + 150y = 9000$
et $x + y = 100$. Nommez ces droites D2 et D3.
Nous allons maintenant représenter graphiquement les points dont les coordonnées vérifient les contraintes.
Pour créer un demi-plan, nous avons besoin d’un point contenu dans celui-ci.
Utilisons l’outil ![]() pour créer le point de coordonnées (-5 ;-5).
pour créer le point de coordonnées (-5 ;-5).
Utilisez le menu Créer - Surface - Demi-plan puis cliquez sur l’axe des abscisses et sur le point de coordonnées (-5 ;-5).
Appuyez sur F9 pour réactiver le même outil.
De le même façon, cliquez sur l’axe des ordonnées puis sur le point de coordonnées (-5 ;-5).
De même utilisez l’outil ![]() pour créer le point de coordonnées (100 ;100).
pour créer le point de coordonnées (100 ;100).
Sans la palette des couleurs, activez la couleur bleue.
Utilisez le menu Créer - Surface - Demi-plan pour créer les demi-plans de bord D1, D2 et D3 et contenant ce dernier point.
Utilisez maintenant l’outil l’outil ![]() pour cacher les points de coordonnées (-5 ;-5) et (100 ;100).
pour cacher les points de coordonnées (-5 ;-5) et (100 ;100).
L’ensemble des points satisfaisant aux contraintes est l’ensemble des points non grisés (bords compris).
Nous allons maintenant créer une fonction de deux variables correspondant au bénéfice. Pour cela utilisez le menu Calculs - Nouveau calcul réel - Fonction réelle de deux variables. Remplir la boîte de dialogue comme ci-dessous :
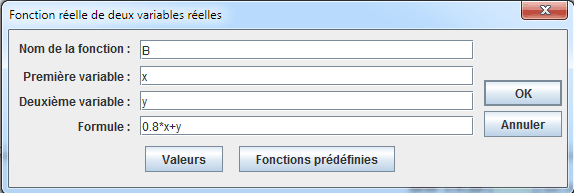
Nous allons maintenant créer la droite correspondant à un bénéfice de 70€.
Pour cela il suffit d’activer l’outil ![]() et d’entrer comme équation B(x,y)=70 (on peut bien sûr aussi entrer 0.8*x+y=70).
et d’entrer comme équation B(x,y)=70 (on peut bien sûr aussi entrer 0.8*x+y=70).
A l’aide de l’outil ![]() créez un point lié à cette droite puis utilisez l’outil
créez un point lié à cette droite puis utilisez l’outil ![]() pour créer un affichage LaTeX lié à ce point. Cliquez sur ce point.
pour créer un affichage LaTeX lié à ce point. Cliquez sur ce point.
Remplir la boîte de dialogue comme ci-dessous.
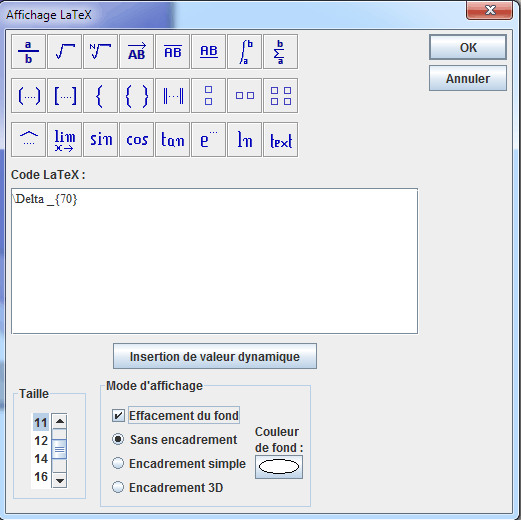
On peut utiliser le bouton Grec et cliquer sur le caractère $\Delta$ pour recopier le code correspondant à al lettre grecque.
Utilisez ensuite l’outil ![]() pour cacher le point lié.
pour cacher le point lié.
A l’aide de l’outil ![]() créez le point d’intersection de la droite D1 avec la droite D2 et le point d’intersection de D1 et D3.
créez le point d’intersection de la droite D1 avec la droite D2 et le point d’intersection de D1 et D3.
A l’aide de l’outil ![]() créez un libre et nommez-le M (outil
créez un libre et nommez-le M (outil ![]() ).
).
Nous allons maintenant mesurer l’abscisse et l’ordonnée de M et créer deux calculs contenant cette abscisse et cette ordonnée.
Activez l’outil ![]() de mesure d’abscisse dans un repère puis cliquez sur le point M. Un message vous avertit que cette mesure est noté xCoord(M,O,I,J).
de mesure d’abscisse dans un repère puis cliquez sur le point M. Un message vous avertit que cette mesure est noté xCoord(M,O,I,J).
Utilisez ensuite l’outil ![]() de création d’un calcul. Entrez comme nom xM et utilisez le bouton Valeurs pour recopier dans le champ Calculs l’abscisse qui vient d’être mesurée.
de création d’un calcul. Entrez comme nom xM et utilisez le bouton Valeurs pour recopier dans le champ Calculs l’abscisse qui vient d’être mesurée.
De même activez l’outil ![]() de mesure d’ordonnée dans un repère puis cliquez sur le point M. Un message vous avertit que cette mesure est noté yCoord(M,O,I,J).
de mesure d’ordonnée dans un repère puis cliquez sur le point M. Un message vous avertit que cette mesure est noté yCoord(M,O,I,J).
Utilisez ensuite l’outil ![]() pour créer un calcul nomme yM contenant cette ordonnée.
pour créer un calcul nomme yM contenant cette ordonnée.
Utilisez l’icône ![]() pour créer les points de coordonnées (xM,0) et (0 ; yM). Dans la palette de style de trait, activer le style de trait pointillé et joindre le point M à ces deux derniers pointsA l’aide de l’outil
pour créer les points de coordonnées (xM,0) et (0 ; yM). Dans la palette de style de trait, activer le style de trait pointillé et joindre le point M à ces deux derniers pointsA l’aide de l’outil ![]() créer un affichage LaTeX lié au premier point avec comme code LaTeX x et un affichage LaTeX lié au deuxième point avec comme code LaTeX y.
créer un affichage LaTeX lié au premier point avec comme code LaTeX x et un affichage LaTeX lié au deuxième point avec comme code LaTeX y.
Nous allons maintenant calculer le bénéfice correspondant aux valeurs de xM et de yM. Pour cela utilisez l’outil ![]() et créez un calcul nommé Ben contenant comme formule B(xM,yM).
et créez un calcul nommé Ben contenant comme formule B(xM,yM).
Créons maintenant en marron la droite $\Delta_{Ben}}$. Pour cela on active le marron dans la palette de couleurs et on utilise l’outil ![]() . On entre dans le champ équation B(x,y)=Ben (ou 0.8*x+y=Ben). La droite apparaît.
. On entre dans le champ équation B(x,y)=Ben (ou 0.8*x+y=Ben). La droite apparaît.
Ben étant l’ordonnée à l’origine de la droite, nous allons créer le point de coordonnées (0,Ben). On utilise pour cela l’outil ![]() et on entre 0 dans le champ Abscisse et Ben dans le champ Ordonnée.
et on entre 0 dans le champ Abscisse et Ben dans le champ Ordonnée.
Nous allons maintenant créer un affichage LaTeX lié à ce dernier point affichant la valeur de Ben. Activez l’outil ![]() et cliquez sur le point. Dans la boîte de dialogue qui s’ouvre, cliquez sur le bouton Insertion de valeur dynamique. Dans la nouvelle boîte de dialogue, cliquez sur Ben et choisir 0 comme nombre de décimales. Validez. Le contenu du code LaTeX est maintenant comme ci-dessous :
et cliquez sur le point. Dans la boîte de dialogue qui s’ouvre, cliquez sur le bouton Insertion de valeur dynamique. Dans la nouvelle boîte de dialogue, cliquez sur Ben et choisir 0 comme nombre de décimales. Validez. Le contenu du code LaTeX est maintenant comme ci-dessous :
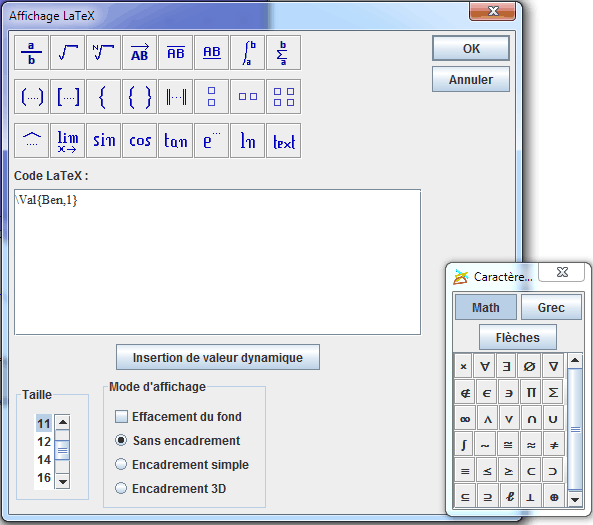
Validez. Vous pouvez déplacer cet affichage avec l’outil ![]() de capture.
de capture.
Nous allons maintenant créer un affichage dynamique des valeurs de xM, yM et Ben dans un affichage LaTeX dynamique. Utilisez pour cela l’outil ![]() .
.
Cliquez d’abord sur le bouton ![]() qui écrit le code nécessaire à un tableau de deux lignes.
qui écrit le code nécessaire à un tableau de deux lignes.
Rajoutez une troisième ligne avec les caractères
\\ {}</code.
Mettez le point d'insertion entre les deux accolades du haut et entrez les caractères <code>x_M = puis cliquez sur le bouton Insertion de valeur dynamique. Dans la boîte de dialogue qui s’ouvre, cliquez sur xM et validez. Le code suivant est ajouté \Val{xM}.
Continuez de façon à remplir le code LaTeX comme ci-dessous puis validez.
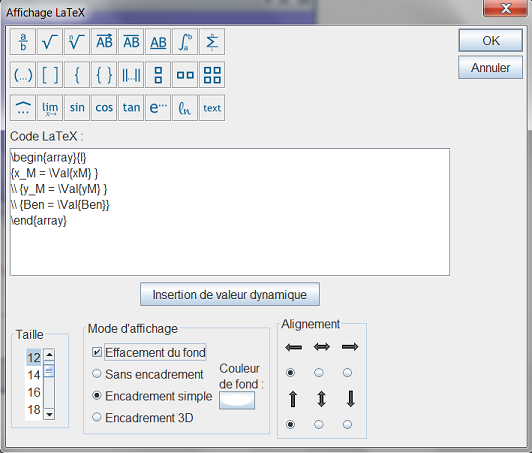
La solution recherchée pour x et y correspond aux coordonnées du point M pour lequel l’ordonnée à l’origine de la droite marron est la plus grande, à condition que M este dans la partie non grisée (bords compris).
En déplaçant le point M on constate que cette ordonnée à l’origine semble maximale lorsque M est confondu avec le point d’intersection des droites D1 et D3.
Le point M est pour l’instant un point libre.
Nous allons demander au logiciel de le transformer en point lié à un autre point.
Utilisez pour cela le menu Modifier- Créer une liaison - Entre un point et un objet puis cliquez sur le point M et ensuite sur le point d’intersection de D1 et D3. Nous voyons que c’est pour cette position de M que notre bénéfice est maximal, qu’il vaut 86 pour xM = 70 et yM = 30.
Notre bénéfice sera donc maximum pour 70 hamburgers "simples" et 30 "maxis".
Voici ci-dessous la figure obtenue avant la liaison entre M et le point d’intersection (vous pouvez capturer M) :
Et la figure finale :
Avec un peu plus de travail et en utilisant des macros d’apparition et de
masquage d’objets on peut obtenir la figure ci-dessous (cliquez sur les macros pour les exécuter) :
Vous pouvez télécharger ces trois figures ci-dessous dans un fichier zippé :