Toutes les versions de cet article : [English] [Español] [français]
Con la nueva versión 4.8 de MathGraph32 es ahora posible crear fractales dinámicos utilizando implementaciones recursivas de construcciones.
Vamos a explicar aquí como hacer un copo de nieve de Von Koch dinámico.
En primer lugar, vamos a crear la construcción que será luego implementada de forma recursiva.
Los nombres de los puntos citados están ahí para una mejor comprensión pero es inútil nominar a los puntos creados.
Creamos una nueva figura en blanco y verificamos que su unidad es el grado (menú Opciones - Figura en curso).
Partiremos de dos puntos libres que llamaremos A y B (icono ![]() ).
).
El primer punto final de nuestra construcción será un clon del punto A. Utilicemos para ello el menú Crear - Clon de objeto y cliqueamos sobre el punto A.
El segundo punto final será un punto situado a un tercio del segmento [AB] a partir de A.
Utilizamos para ello el icono ![]() . Cliqueamos sobre el punto A, centro de la homotecia, elegimos el punto clon, (pero esto no es importante). En la caja de diálogo, ingresamos 1/3 como razón luego cliqueamos sobre el punto B. Llamaremos C al nuevo punto creado.
. Cliqueamos sobre el punto A, centro de la homotecia, elegimos el punto clon, (pero esto no es importante). En la caja de diálogo, ingresamos 1/3 como razón luego cliqueamos sobre el punto B. Llamaremos C al nuevo punto creado.
Creamos ahora la imagen del clon de A en la rotación de centro C y de ángulo –120° (icono ![]() ). Llamaremos a ese punto D.
). Llamaremos a ese punto D.
Creamos ahora el punto medio del segmento [CB] (icono ![]() ). Llamaremos a ese punto E.
). Llamaremos a ese punto E.
Creamos para terminar un punto clon del punto B con el menú Crear - Clon de objeto.
Utilicemos ahora el icono de creación de polígono ![]() . Cliqueamos sobre los puntos C, D y E luego clic con el botón derecho del mouse para cerrar el polígono.
. Cliqueamos sobre los puntos C, D y E luego clic con el botón derecho del mouse para cerrar el polígono.
En la paleta de colores, activamos el color azul. Cliqueamos sobre el icono ![]() de creación de superficie luego cliqueamos sobre el polígono. Ahora ocultamos el polígono (icono
de creación de superficie luego cliqueamos sobre el polígono. Ahora ocultamos el polígono (icono ![]() ).
).
Vamos ahora a crear la construcción. Ella contiene solamente objetos fuentes gráficos
Utilicemos el menú Construcciones - Elección de elementos fuentes - Gráficos. Cliquear, en ese orden, sobre A y B (se trata de puntos libres) luego clic en el botón derecho del mouse para finalizar.
Ahora designamos los objetos finales que son todos gráficos.
Utilicemos el menú Construcciones - Elección de elementos finales- Gráficos. Cliqueamos sobre el clon del punto A, el punto C, el punto D, el punto E, el clon del punto B y sobre la superficie..
Antes de finalizar nuestra construcción vamos a ocultar los puntos finales creados. Utilicemos el icono ![]() para ocultar el clon de A, los puntos C, D y E y el clon de B.
para ocultar el clon de A, los puntos C, D y E y el clon de B.
Ahora utilicemos el menú Construcciones - Finalizar la construcción en curso. Nombremos a esa construcción KochAzul.
Ahora, activamos el color rojo en la paleta de colores y utilizamos el icono ![]() para cambiar el color de la superficie.
para cambiar el color de la superficie.
Utilicemos la herramienta ![]() para dejar nuevamente visibles el clon de A, los puntos C, D, E y el clon de B.
para dejar nuevamente visibles el clon de A, los puntos C, D, E y el clon de B.
Repetimos el mismo procedimiento anterior para crear una construcción llamada KochRojo (no olvidemos ocultar los 5 puntos finales antes de terminar la construcción).
Con la ayuda del menú Construcciones - Guardar una construcción de la figura en un archivo, salvamos las dos construcciones KochAzul y KochRojo en nuestra computadora.
Vamos ahora a crear una macro que implementará esa construcción de manera recursiva en una nueva figura.
Creamos una nueva figura (con unidad de ángulo el grado).
Utilicemos el menú Construcciones - Incorporar una construcción en la figura desde un archivo e incorporemos las dos construcciones precedentes KochAzul y KochRojo en la figura.
Creamos dos puntos libres que llamaremos A y B luego utilizamos la herramienta ![]() para crear un triángulo equilátero directo. Llamemos C al nuevo punto creado.
para crear un triángulo equilátero directo. Llamemos C al nuevo punto creado.
Utilicemos ahora el menú Macros - Nueva macro - Macro de construcción - Recursiva.
Completamos la caja de diálogo como se ve a continuación. Elegimos 4 como profundidad de la recursión.
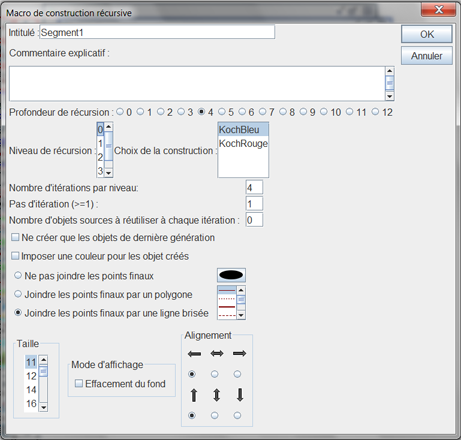
Cliqueando en la lista de los niveles de recursión, afectamos alternativamente las construcciones KochAzul y KochRojo en los niveles 0, 1, 2, 3 y 4. Marcamos la casilla Unir los puntos finales por una poligonal.
Una vez completada la caja, cliqueamos sobre B y luego sobre A (en ese orden).
Una vez completada la caja, cliqueamos sobre B y luego sobre A (en ese orden).
Creamos de la misma manera una segunda macro de construcción recursiva Segmento2 que hará la misma cosa para los puntos A y C, luego una tercera denominada Segmento3 para los puntos C y B.
Salvamos la figura (antes de intentar ejecutar las macros).
Podemos ejecutar las macros para verificar que funcionan bien, pero recordemos que debemos cancelar con la herramienta antes de guardar nuevamente la figura porque una vez ejecutadas las macros, la figura contiene miles de objetos.
Nous allons maintenant expliquer comment faire pour que ces trois macros soient exécutées au chargement de la figure.
Ante todo, es preferible salvar nuevamente la figura bajo un nuevo nombre. Utilicemos el menú Macros - Nueva macro - Ejecución de una sucesión de macros y creamos una macro ejecutante de las tres macros Segmento1, Segmento2 y Segmento3.
Nominemos, por ejemplo, esa macro Inicio.
Ahora, utilizamos el menú Opciones - Figura en curso, cliqueamos sobre la pestaña Macro de arranque y seleccionamos la macro Inicio.
Grabamos nuevamente esa figura y la cerramos.
En el próximo arranque, cuando abramos esta figura, la construcción del copo de nieve será automático.
Pero atención : Si salvamos nuevamente esta figura, el archivo obtenido será muy grande porque, una vez que la macro Inicio sea ejecutada, la figura contendrá decenas de miles de objetos
Atención : También es posible implementar una construcción de manera recursiva sin utilizar la macro del menú Construcción - Implementar una construcción de manera recursiva.
Explicaciones : Retomemos las notaciones de la primera figura.
La construcción es ante todo aplicada al nivel 0 : cuatro puntos son creados y la superficie. Seguidamente la construcción se llama otra vez para los puntos clones de A y C, luego C y D, luego D y E, luego E y el clon de D. Pero, en cada llamado, la construcción se llama asimismo para los puntos creados y hasta la profundidad requerida.
El paso de la iteración es 1 puesto que, una vez que la construcción se llama por ejemplo para los puntos clones de A y C se llama seguidamente para C y D y así sucesivamente. Se salta entonces a un objeto final cada vez antes de reimplantar la construcción allí cuatro veces seguidas. El número de iteraciones por nivel es entonces 4..
Como habíamos pedido, los puntos creados en la última generación están todos unidos por una poligonal.