Création d’une courbe de fonction
Liaison d’un point à une courbe de fonction
Création d’un point sur une courbe de fonction à postériori
Courbe définie par points et tangentes
Pour créer une courbe de fonction, une fonction numérique réelle doit avoir été définie et la figure doit posséder au moins un repère.
Le plus simple en partant d’une figure vierge est d’utiliser l’icône ![]() puis de choisir un type de figure avec repère (en prenant garde de choisir l’unité d’angle voulue).
puis de choisir un type de figure avec repère (en prenant garde de choisir l’unité d’angle voulue).
On crée la fonction à l’aide de l’icône ![]() de la barre d’icônes déroulante des lieux.
de la barre d’icônes déroulante des lieux.
Cette boîte de dialogue comprend une case à cocher nommée Tracer courbe. Si cette case est cochée, la courbe de la fonction sera automatiquement tracée dans le repère choisi. Dans ce cas la fonction est considérée comme définie sur R.
Si on n’a pas coché la case Tracer courbe dans la boîte de dialogue de création d’une fonction, on peut créer la courbe à postériori.
On crée la courbe d’une fonction en cliquant sur l’icône ![]() .
.
Une boîte de dialogue s’ouvre analogue à celle qui figure ci-dessous.
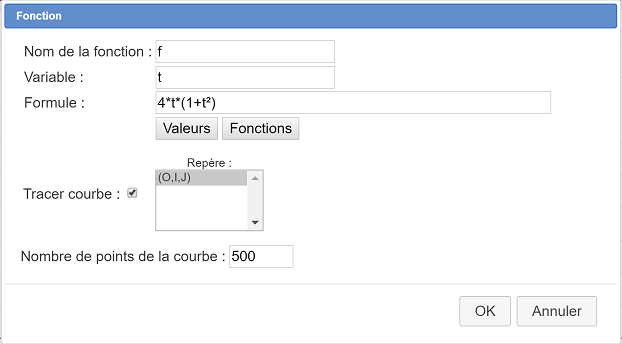
Par défaut il est supposé que vous voulez tracer votre courbe pour une fonction définie pour tout réel x, mais vous pouvez aussi tracer la courbe sur un intervalle borné ou non.
Si, par exemple, vous voulez tracer la courbe sur un intervalle [a ;b], cliquez sur le bouton ][a ;b][.
La boîte de dialogue se modifie comme ci-dessous et vous pouvez alors entrer les valeurs de a et b. Ces valeurs peuvent être des constantes ou des calculs utilisant les valeurs précédemment définies.
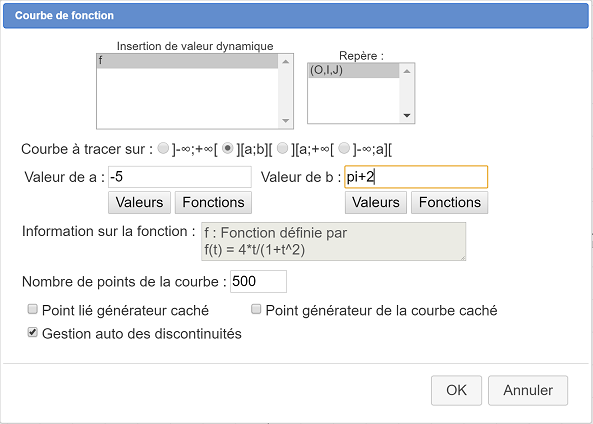
Expliquons maintenant les champs contenus dans cette boîte de dialogue.
Pour cela il faut comprendre comment MathGraph32 trace une courbe de fonction.
Dans le cas d’une courbe demandée sur R, le logiciel commence par créer un point lié à l’axe des abscisses. Ce point est appelé le point lié générateur. Vous pouvez changer son nom dans la boîte de dialogue.
MathGraph32 mesure alors l’abscisse de ce point dans le repère choisi et crée un crée un calcul contenant cette abscisse (x1 par défaut si ce nom est libre). Vous pouvez changer ce nom dans le champ Nom de l’abscisse du point lié générateur.
MathGraph32 crée ensuite un calcul contenant l’image de cette abscisse (y1 par défaut si ce nom est libre défini donc comme f(x1)).
Il crée enfin un point de coordonnées (x1 ; y1) et la courbe est créée comme lieu de ce point généré par les déplacements du point lié générateur.
Le point lié générateur de la courbe et le point générateur de la courbe sont visibles par défaut. Vous pouvez les masquer en cochant les cases correspondantes.
Par défaut, la case à cocher Gestion auto des discontinuités est cochée. MathGraph32 essaiera alors de détecter les endroits où la courbe est discontinue. Si cela ne fonctionne pas correctement, augmentez le nombre de points de la courbe ou tracez la courbe sur plusieurs intervalles successifs.
Dans la cas d’une fonction définie sur un intervalle [a ;b], MathGraph32 crée d’abord deux points de coordonnées (a ;0) et (b ;0) puis le segment les joignant. Le point lié générateur est alors lié à ce segment.
Dans le cas d’un intervalle non borné, MathGraph32 procède de la même façon en liant le point à une demi-droite.
Il est possible de créer un point lié à un lieu de points donc à une courbe de fonction.
Une fois la courbe créée, cliquez simplement sur l’icône ![]() puis sur la courbe pour créer un point lié à celle-ci. Remarquez que ce point lié peut lui même être utilisé pour générer un lieu de points.
puis sur la courbe pour créer un point lié à celle-ci. Remarquez que ce point lié peut lui même être utilisé pour générer un lieu de points.
Il peut être utile de créer un point mobile sur une courbe de fonction après avoir créé la courbe.
Imaginons par exemple que nous avons créé la courbe de la fonction f définie par sur R par $f(x) = \frac{4x}{1+x^2}$.
Nous avons d’abord créé la fonction en décochant la case Tracer courbe puis nous avons utilisé l’icône ![]() en décochant les cases Point lié générateur caché et Point générateur de la courbe caché.
en décochant les cases Point lié générateur caché et Point générateur de la courbe caché.
Nous créons maintenant la courbe d’une fonction g définie par $g(x)=\frac{1}{x}$ en cliquant sur l’icône ![]() . Cochez la case Tracer courbe et validez.
. Cochez la case Tracer courbe et validez.
La courbe de la fonction g apparaît.
Nous souhaitons maintenant avoir un point sur la courbe de g ayant la même abscisse x1 que le point générateur de la courbe de f.
Utilisez pour cela l’icône ![]() de création d’un point par ses coordonnées.
de création d’un point par ses coordonnées.
Remplissez la boîte de dialogue comme ci-dessous.
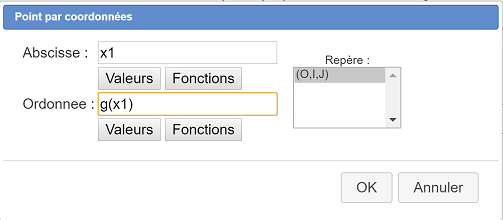
Un nouveau point apparaît sur le courbe comme ci-dessous.
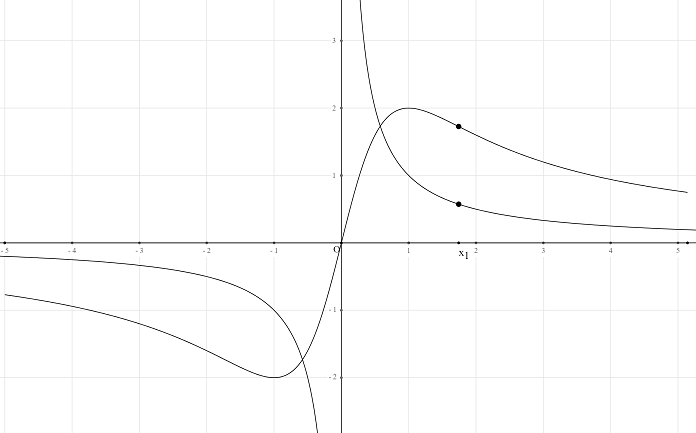
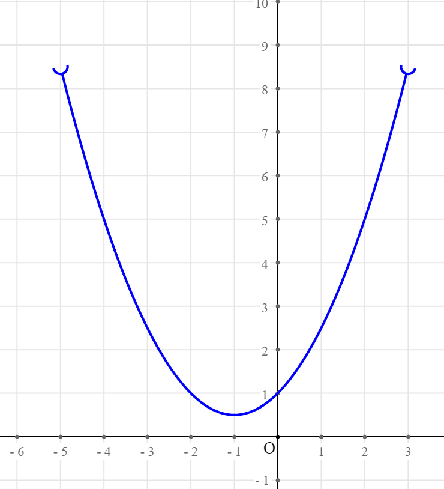
Pour le cas de fonctions discontinues vous pouvez aussi créer des courbes de fonctions avec crochets avec l’icône  comme ci-dessous par exemple :
comme ci-dessous par exemple :
Vous pouvez aussi avec l’outil  créer une courbe de fonction en donnant des points de la courbe (jusqu’à 10 points) et en donnant les coefficients directeurs des tangentes en ces points.
créer une courbe de fonction en donnant des points de la courbe (jusqu’à 10 points) et en donnant les coefficients directeurs des tangentes en ces points.
Vous pouvez obtenir avec l’outil  la courbe d’une fonction polynomiale en cliquant sur des points de la courbe (de 3 à 7 points).
la courbe d’une fonction polynomiale en cliquant sur des points de la courbe (de 3 à 7 points).