Toutes les versions de cet article : [Español] [français]
Nous sommes à la recherche d’une approximation de courbe possédant la propriété suivante : Les points F et G étant donnés, une demi-droite parallèle à un axe donné (FG) se réfléchit sur cette courbe en passant par le point F comme illustré sur la figure ci-dessous.
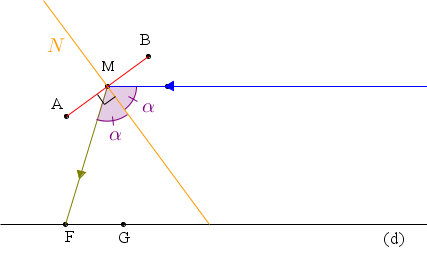
Pour cela nous allons créer une construction que nous implémenterons ensuite de façon itérative.
Créez une nouvelle figure vierge (munie d’un segment longueur unité, sans repère) avec l’icône ![]() . Eloignez le point V du point U pour que la longueur unité soit plus grande qu’elle l’est par défaut.
. Eloignez le point V du point U pour que la longueur unité soit plus grande qu’elle l’est par défaut.
Commencez par créer trois points libres avec l’icône ![]() que vous nommerez F, G et M. Arrangez-vous pour que la droite (FG) soit proche d’une droite horizontale comme ci-dessus.
que vous nommerez F, G et M. Arrangez-vous pour que la droite (FG) soit proche d’une droite horizontale comme ci-dessus.
Utilisez ensuite l’icône ![]() pour créer l’image du point M par la translation de vecteur $\overrightarrow{FG}$ que nous nommerons G’. Pour cela cliquez successivement sur F, G puis sur M.
pour créer l’image du point M par la translation de vecteur $\overrightarrow{FG}$ que nous nommerons G’. Pour cela cliquez successivement sur F, G puis sur M.
Créez la demi-droite d’origine M passant par G’ (icône ![]() ) et le segment [MG] (icône
) et le segment [MG] (icône ![]() )
)
Maintenant utilisez l’icône ![]() pour créer la bissectrice de l’angle FMG’ (cliquez successivement sur F, M et G’).
pour créer la bissectrice de l’angle FMG’ (cliquez successivement sur F, M et G’).
Utilisez l’icône ![]() pour créer la droite perpendiculaire à cette bissectrice passant par M.
pour créer la droite perpendiculaire à cette bissectrice passant par M.
A l’aide de l’icône ![]() créez le cercle de centre M et rayon 0,25.
créez le cercle de centre M et rayon 0,25.
Créez maintenant les deux points d’intersection de ce cercle avec la droite perpendiculaire précédemment tracée avec l’icône ![]() (il suffit de cliquer à l’intersection des deux ou sur la droite puis sur le cercle).
(il suffit de cliquer à l’intersection des deux ou sur la droite puis sur le cercle).
Ne nommez pas ces deux points.
Pour une meilleur visualisation, activez la couleur rouge dans la palette de couleur.
Créez maintenant le segment joignant les deux points d’intersection (icône ![]() ).
).
Nous allons maintenant créer une macro-construction qui, partir des points F, G et M (objets sources) créera le segment rouge et un des deux points d’intersection (celui nommé A sur la figure ci-dessus). Ces deux objets seront les objets finaux.
Utilisez le menu Construction - Choix des objets sources puis cliquez successivement sur F, G et M.
Utilisez maintenant le menu Construction - Choix des objets finaux puis cliquez sur le segment rouge et sur un des deux points d’intersection (celui nommé A sur la figure ci-dessus).
Maintenant finissons notre construction avec le menu Construction - Finir la construction en cours. Une boîte de dialogue s’ouvre : Nommez cette construction Cons et validez.
Pour comprendre comment fonctionne cette construction :
– Créez un nouveau point libre N (icône ![]() ) que nous appellerons N.
) que nous appellerons N.
– Utilisez le menu Construction - Implémenter une construction de la figure. Sélectionnez la construction Const, validez puis cliquez sur le point N
Vous voyez que MathGraph32 a construit un segment rouge et un nouveau point.
L’idée est de recommencer avec ce nouveau point et ainsi de suite un grand nombre de fois.
Pour cela nous allons utiliser une des fonctions avancées de MathGraph32 : La possibilité d’implémenter une construction de façon itérative.
Créez un nouveau point libre que nous appellerons P.
Utilisez maintenant le menu Construction - Implémenter une construction de façon itérative.
Une boîte de dialogue s’ouvre. Remplissez-là comme ci-dessous.
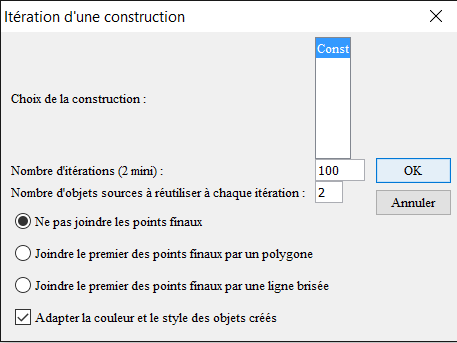
Cliquez ensuite successivement sur les points F, G et M.
Les points F et G sont utilisés comme les deux premiers objets sources de chaque implémentation de construction, le troisième étant ensuite le point d’intersection créé lors de chaque construction. Il faut noter que pour que cela fonctionne ce point d’intersection devait être le premier de nos objets finaux créés.
Voici ci-dessous la figure obtenue (pour voir une plus grosse partie de la "courbe" crée, vous pouvez rapprocher le point V du point U) :
Utilisez l’icône ![]() pour créer une nouvelle figure munie d’un repère orthonormal.
pour créer une nouvelle figure munie d’un repère orthonormal.
Utilisez l’icône ![]() pour créer la fonction f définie par f $x : \mapsto x^2$ et sa courbe représentative.
pour créer la fonction f définie par f $x : \mapsto x^2$ et sa courbe représentative.
Créez un point lié à cette courbe (icône ![]() ) et nommez-le A.
) et nommez-le A.
Mesurez l’abscisse du point A dans le repère (icône ![]() ) et nommez-là a.
) et nommez-là a.
Pour créer la tangente en A à la parabole, utilisez l’icône ![]() (dans les icônes de création de droites).
(dans les icônes de création de droites).
Remplissez la boîte de dialogue comme ci-dessous :
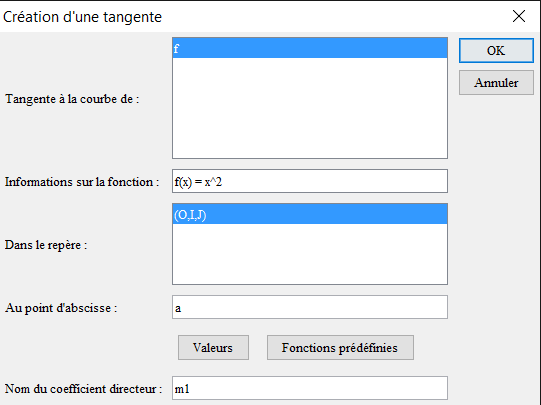
Créez ensuite la perpendiculaire à cette tangente en A avec l’icône ![]() (c’est la normale à la courbe en A).
(c’est la normale à la courbe en A).
Utilisez l’icône ![]() pour créer l’image A’ du point A par la translation de vecteur de coordonnées (0 ; 1).
pour créer l’image A’ du point A par la translation de vecteur de coordonnées (0 ; 1).
Créez la demi-droite [AA’) (icône ![]() ).
).
Utilisez ensuite l’icône ![]() pour créer l’image de cette demi-droite dans la symétrie orthogonale par rapport à la normale (cliquer d’abord sur l’axe de symétrie puis sur la demi-droite).
pour créer l’image de cette demi-droite dans la symétrie orthogonale par rapport à la normale (cliquer d’abord sur l’axe de symétrie puis sur la demi-droite).
Avec l’icône ![]() créez l’intersection de la demi-droite image avec l’axe des ordonnées. Nommer F le point d’intersection.
créez l’intersection de la demi-droite image avec l’axe des ordonnées. Nommer F le point d’intersection.
Capturez le point A. On peut constater que la position de F ne dépend pas de A.
Voici ci-dessous la figure obtenue :