Toutes les versions de cet article : [Español] [français]
Buscamos una aproximación de una curva con la siguiente propiedad : Los puntos F y G están dados, una semirrecta paralela a un eje dado (FG) se refleja sobre esa curva pasando por el punto F, como se muestra la figura siguiente.
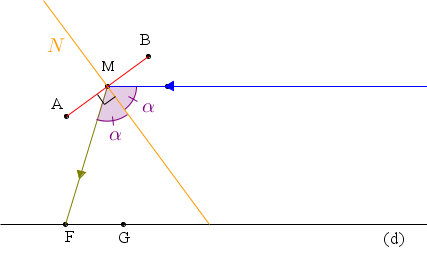
Para ello vamos a crear una construcción que vamos a aplicar a continuación, de manera iterativa.
Creamos una nueva figura en blanco (con un segmento de longitud unidad y sin referencial) con el icono ![]() . Alejemos el punto V del punto U para aumentar la unidad de longitud que está por defecto.
. Alejemos el punto V del punto U para aumentar la unidad de longitud que está por defecto.
Comenzamos por crear tres puntos libres con el icono ![]() que nombraremos F, G y M. Manipulemos la recta (FG) para aproximarla a una recta horizontal como arriba.
que nombraremos F, G y M. Manipulemos la recta (FG) para aproximarla a una recta horizontal como arriba.
A continuación, utilicemos el icono ![]() para crear la imagen del punto M por la traslación de vector $\overrightarrow{FG}$ que llamaremos G’. Para ello cliqueamos sucesivamente en F, G y M.
para crear la imagen del punto M por la traslación de vector $\overrightarrow{FG}$ que llamaremos G’. Para ello cliqueamos sucesivamente en F, G y M.
Creamos la semirrecta de origen M que pasa por G’ (icono ![]() ) y el segmento [MG] (icono
) y el segmento [MG] (icono ![]() )
)
Ahora utilizamos el ícono ![]() para crear la bisectriz del ánguloFMG’ (cliqueamos sucesivamente sobre F, M et G’).
para crear la bisectriz del ánguloFMG’ (cliqueamos sucesivamente sobre F, M et G’).
Utilizamos el ícono ![]() para crear la recta perpendicular a esa bisectriz que pasa por M.
para crear la recta perpendicular a esa bisectriz que pasa por M.
Con la ayuda del ícono ![]() creamos la circunferencia de centro M y radio 0,25.
creamos la circunferencia de centro M y radio 0,25.
Creamos ahora los dos puntos de intersección de esa circunferencia con la recta perpendicular precedentemente trazada con el ícono ![]() (alcanza cliquear en la intersección de las dos o sobre la recta y luego sobre la circunferencia).
(alcanza cliquear en la intersección de las dos o sobre la recta y luego sobre la circunferencia).
No nominaremos a esos dos puntos.
Para una mejor visualización, activemos el color rojo en la paleta de color.
Creamos ahora el segmento que une los dos puntos de intersección (ícono ![]() ).
).
Ahora vamos a crear una macro-construcción que, partiendo de los puntos F, G y M (objetos fuentes), creará el segmento rojo y uno de los dos puntos de intersección (el nominado A en la figura anterior). Estos dos objetos serán los objetos finales.
Utilizamos el menú Construcciones - Elección de elementos fuentes luego cliqueamos sucesivamente sobre F, G y M.
Utilizamos ahora el menú Construcciones - Elección de elementos finales luego cliqueamos sobre el segmento rojo y sobre uno de los dos puntos de intersección (el llamado A en la figura anterior).
Ahora terminamos nuestra construcción con el menú Construcciones - Finalizar la construcción en curso. Un cuadro de diálogo se abre : Nominamos esa construcción Cons y validamos.
Para comprender cómo funciona esa construcción :
– Creamos un nuevo punto libre N (ícono ![]() ) que llamaremos N.
) que llamaremos N.
– Utilizamos el menú Construcciones - Implementar una construcción de la figura. Selectionamos la construcción Const, validamos y luego cliqueamos sobre el punto N.
Veremos que MathGraph32 ha construido un segmento rojo y un nuevo punto.
La idea es recomenzar con ese nuevo punto y así sucesivamente un gran número de veces.
Para ello vamos a utilizar una de las funciones avanzadas de MathGraph32 : La posibilidad de implementar una construcción iterativa.
Creamos un nuevo punto libre que llamaremos P.
Utilizamos ahora el menú Construcciones - Implementar una construcción de manera iterativa.
Un cuadro de diálogo se abre. Lo completamos como se ve a continuación.
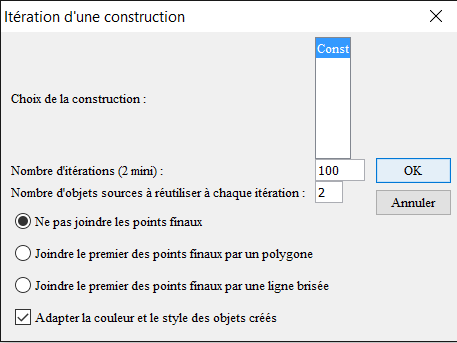
Cliqueamos a continuación sucesivamente sobre los puntos F, G y M.
Los puntos F y G se utilizan como los dos primeros objetos fuentes de cada implementación de la construcción, el tercero es entonces el punto de intersección creado luego de cada construcción. Debemos tener en cuenta que para que esto funcione ese punto de intersección debe ser el primero de nuestros objetos finales creados.
Aquí debajo está la figura obtenida (para ver una porción mayor de la "curva" creada, se puede aproximar el punto V al punto U) :
Utilizemos el ícono ![]() para crear una nueva figura dotada de un referencial ortonormall.
para crear una nueva figura dotada de un referencial ortonormall.
Utilizemos el ícono ![]() para crear la función f definida por f $x : \mapsto x^2$ y su curva representativa.
para crear la función f definida por f $x : \mapsto x^2$ y su curva representativa.
Creamos un punto ligado a esa curva (icono ![]() ) y lo llamamos A.
) y lo llamamos A.
Medimos la abscisa del punto A en el referencial (icono ![]() ) y la llamamos a.
) y la llamamos a.
Para crear la tangente en A a la parábola utilizamos el icono ![]() (en los iconos de creación de rectas).
(en los iconos de creación de rectas).
Rellenamos el cuadro de diálogo como se muestra a continuación :
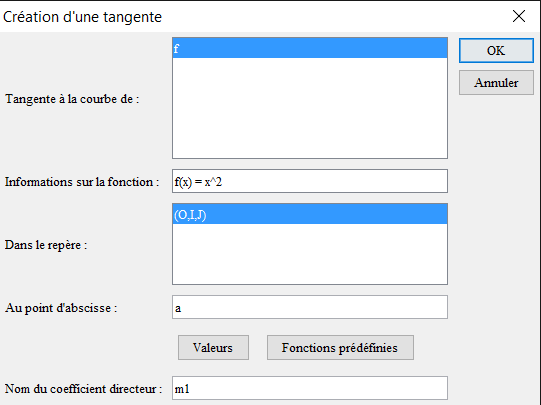
Creamos a continuación la perpendicular a esa tangente en A con el icono ![]() (esta es la normal a la curva en A).
(esta es la normal a la curva en A).
Utilizamos el icono ![]() para crear la imagen A’ del punto A por la traslación de vector de coordenadas (0, 1).
para crear la imagen A’ del punto A por la traslación de vector de coordenadas (0, 1).
Creamos la semirrecta [AA’) (icono ![]() ).
).
Utilizamos a continuación ![]() para crear la imagen de esa semirrecta en la simetría axial respecto a la normal (primero hacemos clic en el eje de simetría y luego en la semirrecta).
para crear la imagen de esa semirrecta en la simetría axial respecto a la normal (primero hacemos clic en el eje de simetría y luego en la semirrecta).
Con el icono ![]() creamos la intersección de la semirrecta imagen con el eje de ordenadas. Designamos con F el punto de intersección.
creamos la intersección de la semirrecta imagen con el eje de ordenadas. Designamos con F el punto de intersección.
Capturemos el punto A. Se puede constatar que la posición de F no depende de A.
Aquí está debajo la figura obtenida :