Toutes les versions de cet article : [Español] [français]
Cet article a été revu et adapté à la version Javascipt de MathGraph32. Vous devez utiliser une version 7.3.5 ou ultérieure.
Dans cet article nous allons expliquer comment utiliser des constructions de façon récursive pour obtenir une version simplifiée de la figure ci-dessous.
Une figure complète exploitable est disponible ici :
Nous allons pour cela créer deux constructions que nous implémenterons de façon récursive.
Remarque préliminaire : Si vous avez échoué à créer vos constructions (étapes 1 et 3), vous pouvez les télécharger ci-dessous, les décompresser dans un dossier de votre disque dur et utiliser ces fichiers au lieu de ceux que vous êtes censés avoir créés par vos propres moyens
Créez une figure vierge (avec longueur unité) avec l’icône  .
.
Assurez-vous avec l’icône  que l’unité d’angle de la figure est bien le degré.
que l’unité d’angle de la figure est bien le degré.
A l’aide de l’icône  (création d’un calcul réel), créez six calculs (dans cet ordre) :
(création d’un calcul réel), créez six calculs (dans cet ordre) :
– Un calcul nommé coefRay avec comme formule 0.7
– Un calcul nommé coefAng avec comme formule 0.7
– Un calcul nommé p avec comme formule 0.25
– Un calcul nommé nbsDem avec comme formule 1
– Un calcul nommé n avec comme formule 0
– Un calcul nommé ray avec comme formule 4.8
– Un calcul nommé ang avec comme formule 45
Créez un point libre que nous appellerons A avec l’icône  . Placez-le à gauche et au milieu de la figure.
. Placez-le à gauche et au milieu de la figure.
Avec l’icône  créez une droite horizontale passant par A.
créez une droite horizontale passant par A.
Utilisez l’icône  pour créer le cercle de centre A et de rayon ray.
pour créer le cercle de centre A et de rayon ray.
Utilisez l’icône  pour créer l’intersection de la droite horizontale avec ce cercle (cliquez quand vous voyez affiché cette intersection).
pour créer l’intersection de la droite horizontale avec ce cercle (cliquez quand vous voyez affiché cette intersection).
Utilisez l’outil rotation  pour créer l’image B du dernier point créé par la rotation de centre A et d’angle ang (cliquez d’abord sur le centre A de la rotation, entrez ang comme angle puis cliquez sur le dernier point créé).
pour créer l’image B du dernier point créé par la rotation de centre A et d’angle ang (cliquez d’abord sur le centre A de la rotation, entrez ang comme angle puis cliquez sur le dernier point créé).
Utilisez l’outil symétrie axiale  pour créer l’image C du point B dans la symétrie axiale par rapport à la droite horizontale (il faut cliquer d’abord sur l’axe de symétrie puis sur le point dont on veut créer l’image).
pour créer l’image C du point B dans la symétrie axiale par rapport à la droite horizontale (il faut cliquer d’abord sur l’axe de symétrie puis sur le point dont on veut créer l’image).
Créez maintenant une droite horizontale passant par B (icône  ).
).
Créez maintenant, dans cet ordre, quatre calculs réels ( ) :
) :
– Un calcul nommé q avec comme formule 1-p
– Un calcul nommé n1 avec comme formule n+1
– Un calcul nommé ray1 avec comme formule ray*coefRay
– Un calcul nommé ang1 avec comme formule ang*coefAng
Utilisez maintenant l’icône  pour créer un point D lié à la droite horizontale passant par B (comme ci-dessous).
pour créer un point D lié à la droite horizontale passant par B (comme ci-dessous).
Créez dans cet ordre, trois calculs réels ( ) :
) :
– Un calcul nommé n2 avec comme formule n+1
– Un calcul nommé ray2 avec comme formule ray*coefRay
– Un calcul nommé ang2 avec comme formule ang*coefAng
Utilisez l’outil symétrie axiale  pour créer l’image E du point D dans la symétrie axiale par rapport à la droite horizontale passant par A.
pour créer l’image E du point D dans la symétrie axiale par rapport à la droite horizontale passant par A.
Dans la palette de style de flèches, activez la petite flèche pleine.
Utilisez l’icône  pour créer les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$.
pour créer les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$.
Avec l’icône  créez les milieux des segments [AB] et [AC].
créez les milieux des segments [AB] et [AC].
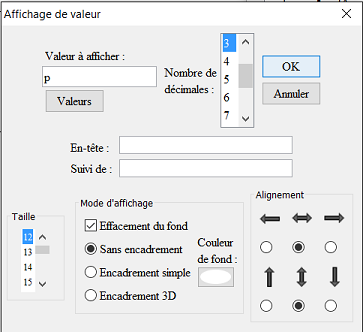
Créez maintenant en bleu un affichage de la valeur de p lié au milieu du segment [AB]. Pour cela, utilisez l’icône  , cliquez sur le milieu puis remplissez la boîte de dialogue comme ci-dessous (3 décimales demandées et un affichage centré horizontalement et verticalement) :
, cliquez sur le milieu puis remplissez la boîte de dialogue comme ci-dessous (3 décimales demandées et un affichage centré horizontalement et verticalement) :
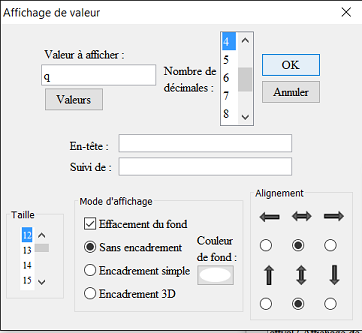
De même créez en vert un affichage de la valeur de q lié au milieu de [AC] :
Créez maintenant les milieux des segments [BD] et [CE] (icône  ).
).
Nous allons maintenant créer en bleu un affichage LaTeX lié au milieu de [BD] avec l’icône  . Pour cela cliquez sur le milieu de [BD] puis remplissez la boîte de dialogue comme ci-dessous. Le code LaTeX est
. Pour cela cliquez sur le milieu de [BD] puis remplissez la boîte de dialogue comme ci-dessous. Le code LaTeX est S_{\Val{n1}}. \Val{n1} est un code LaTeX spécifique à MathGraph32 qui demande un affichage dynamique de la valeur de n1 (avec deux décimales par défaut ce qui ici importe peu car n1 est entier) . On obtiendra ainsi la lettre S avec comme indice la valeur de n1 :
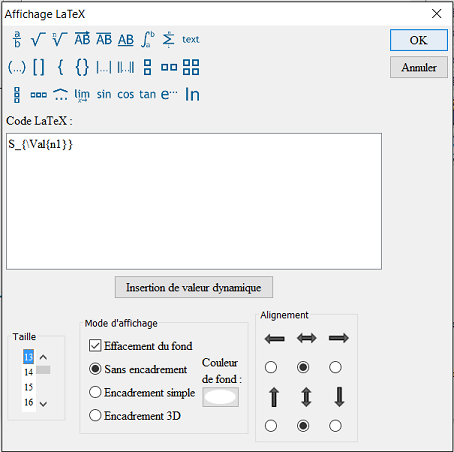
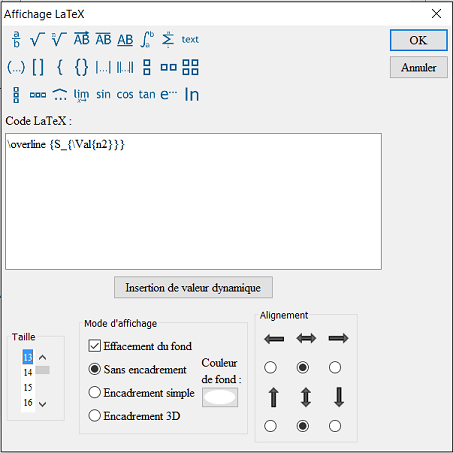
Créez de même en vert un affichage LaTeX lié au milieu de [CE] comme ci-dessous. Le code LaTeX est \overline {S_{\Val{n2}}}. Il affichera, sous une barre, la lettre S avec comme indice la valeur de n2 :
Notre figure est prête pour créer notre première construction.
Il est important que les objets aient bien été créés dans l’ordre que nous avons indiqué. Si l’ordre n’est pas le bon, la macro ne pourra pas être implémentée de façon itérative. Vous pouvez modifier cet ordre en utilisant le protocole de la figure (icone  de la arre d’outils supérieure). Dans cette boîte de dialogue, les flèches de droite permettent de remonter ou descendre un objet dans la liste des objets créés.
de la arre d’outils supérieure). Dans cette boîte de dialogue, les flèches de droite permettent de remonter ou descendre un objet dans la liste des objets créés.
Utilisez l’outil  pour masquer les milieux de [BD] et [CE].
pour masquer les milieux de [BD] et [CE].
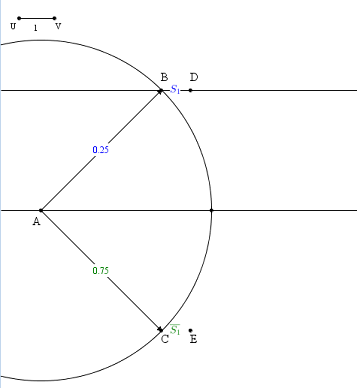
A ce stade votre figure doit ressembler à la figure ci-dessous :
Passons à la création de la construction. Pour gérer les constructions utilisez l’icône  qui fait apparaître des icônes supplémentaires.
qui fait apparaître des icônes supplémentaires.
Cliquez sur l’icône  (création d’une construction) puis choisissez l’item Choix des objets sources numériques.
(création d’une construction) puis choisissez l’item Choix des objets sources numériques.
Au début vous obtenez la boîte de dialogue ci-dessous (l’ordre des éléments à gauche doit être le même) :
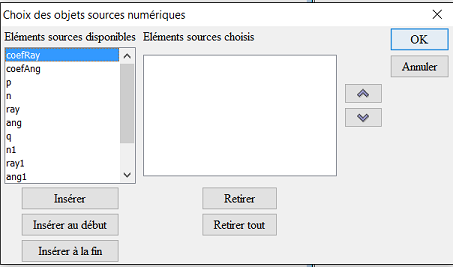
Cliquez sur le bouton Insérer (ou double-cliquez sur chaque valeur) pour obtenir ceci :
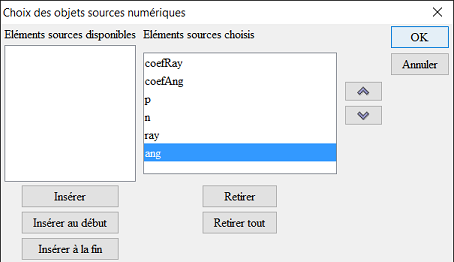
Désignons maintenant les objets sources graphiques : Il n’y en a qu’un : le point A.
Utilisez de nouveau l’icône  , choisissez l’item Choix des objets sources graphiques puis cliquez sur le point A qui se met à clignoter.
, choisissez l’item Choix des objets sources graphiques puis cliquez sur le point A qui se met à clignoter.
En bas et à droite de la fenêtre, cliquez sur l’icône rouge STOP pour indiquer que tous les objets sources graphiques ont été désignés.
Désignons maintenant les objets finaux numériques.
Utilisez de nouveau l’icône  , choisissez l’item Choix des objets finaux numériques.
, choisissez l’item Choix des objets finaux numériques.
Cliquez sur n1 puis cliquez sur ang2 de façon à obtenir ce qui suit :
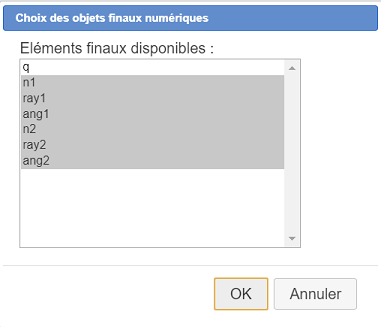
Reste à choisir les objets finaux graphiques.
Utilisez de nouveau l’icône  , choisissez l’item Choix des objets finaux graphiques.
, choisissez l’item Choix des objets finaux graphiques.
Cliquez sur :
- les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$
- Les deux affichages de valeurs liés aux milieux de [AB] et [AC]
- Les deux affichages LaTex
- Les points D et E
Cliquez sur le bouton rouge STOP pour indiquer que vous avez fini de désigner les objets finaux graphiques.
Avant de finir la construction, masquez les points D et E avec l’outil  .
.
Il nous reste à finaliser notre construction.
Utilisez de nouveau l’icône  , choisissez l’item Finir la construction en cours.
, choisissez l’item Finir la construction en cours.
Remplissez la boîte de dialogue comme ci-dessous. Le champ Information sert à renseigner l’utilisateur lorsqu’il utilise la construction .
Voici son contenu si vous voulez le copier-coller :
#1:Valeur de coefRay (coefficient de réduction à chaque étape pour la longueur des flèches)
#2:Valeur de coefAng (coefficient de réduction à chaque étape pour l'angle des flèches avec l'horizontale)
#3:Valeur de p (probabilité de succès)
#4:Valeur de n (le rang de génération de branche)
#5:Le rayon de départ (longueur des flèches)
#6:L'angle de départ en degrés de la première flèche avec l'horizontale
##7:Le point origine de l'arbre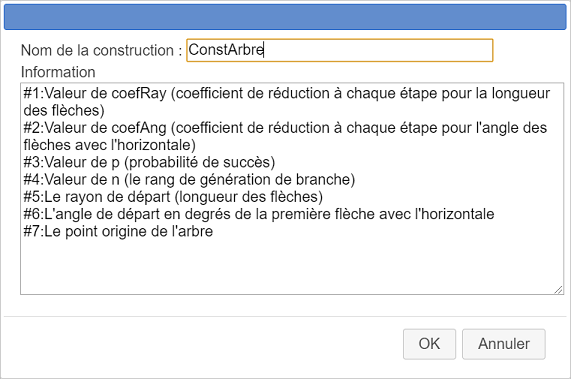
Enregistrez la figure à l’emplacement de votre choix par sécurité. Nous l’appellerons ArbreBinomial1.
Pour enregistrer la construction dans un fichier séparé, utilisez l’icône  et choisissez l’item Enregistrer une construction de la figure. Enregistrez la construction ConstArbre à l’emplacement de votre choix.
et choisissez l’item Enregistrer une construction de la figure. Enregistrez la construction ConstArbre à l’emplacement de votre choix.
Quelques explications : Cette construction sera implémentée de façon récursive. Les objets sources doivent figurer dans la figure en premier dans la liste des objets créés. Ce sont pour nous : coefRay, coefAngle, p, n, ray, ang. Les trois premiers seront communs à toutes les implémentations. Le seul objet source graphique est le point initial de l’arbre. Lors des implémentations successives, les objets sources non communs seront remplacés par les premiers objets finaux. La construction sera de nouveau implémentée pour n1, ray1, ang1, le point B, puis pour n2, ray2, ang2, le point C et le pas sera de 4 car on saute 4 objets finaux pour passer de n1 à n2.
Créez une nouvelle figure qui contiendra notre figure finale (sans repère et avec longueur unité). Vérifiez qu’elle utilise bien le degré comme unité d’angle.
Créez un point libre au milieu et à gauche de la figure.
Créez les calculs suivants (dans cet ordre) :
– Un calcul nommé coefRay avec comme formule 0.7
– Un calcul nommé coefAng avec comme formule 0.7
– Un calcul nommé p avec comme formule 0.25
– Un calcul nommé nbsDem avec comme formule 1 (il ne servira qu’à l’étape 4)
– Un calcul nommé n avec comme formule 0
– Un calcul nommé ray avec comme formule 4.8
– Un calcul nommé ang avec comme formule 45
Utilisez de nouveau l’icône  , choisissez ll’item Incorporer une construction depuis un fichier et incorporez dans cette figure la construction ConstArbre.
, choisissez ll’item Incorporer une construction depuis un fichier et incorporez dans cette figure la construction ConstArbre.
Nous allons maintenant créer une macro chargée d’implémenter cette construction de façon récursive.
Déroulez la barre de menu des affichages et, à sa droite, cliquez sur l’outil  , et choisissez en bas de la liste Macro d’implémentation récursive, puis cliquez en haut et à gauche de la figure pour désigner l’emplacement de son intitulé.
, et choisissez en bas de la liste Macro d’implémentation récursive, puis cliquez en haut et à gauche de la figure pour désigner l’emplacement de son intitulé.
Remplissez la première boîte de dialogue comme ci-dessous :
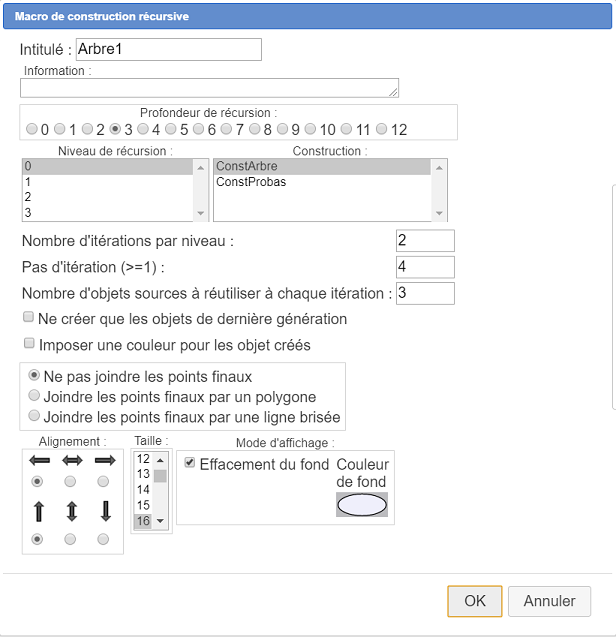
Une deuxième boîte de dialogue s’ouvre. Vous devez affecter les objets sources.
Affectez à l’objet source numéro 1 le calcul coefRay comme ci-dessous :
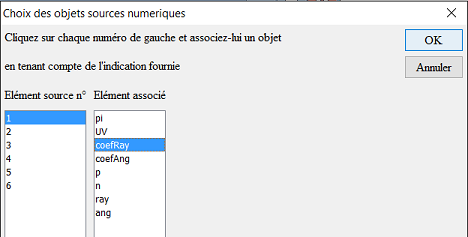
De même affectez :
– A l’élément source n° 2 le calcul coefAng
– A l’élément source n° 3 le calcul p
– A l’élément source n° 4 le calcul n
– A l’élément source n° 5 le calcul ray
– A l’élément source n° 6 le calcul ang
Validez. Il vous est maintenant demandé de cliquer sur le point origine de l’arbre. Cliquez sur le point libre que vous avez créé.
La macro apparaît. En cliquant sur son intitulé vous devez voir apparaître l’arbre binomial. Si cela fonctionne bien annulez l’exécution de cette macro (icône  ).
).
Enregistrez cette figure à l’emplacement de votre choix. Nous l’appellerons ArbreBinomialFinal.
Reprenez la figure ArbreBinomial1. Nous allons la modifier pour créer une autre construction qui elle sera chargée d’afficher les probabilités au bout des branches.
Utilisez l’outil  pour démasquer les points D et E.
pour démasquer les points D et E.
Utilisez l’icône  pour créer un nouveau calcul nommé nbsDem contenant comme formule 1. Ce calcul fera partie des objets sources communs à toutes les implémentations. Il faut donc le reclasser. Pour cela utilisez le protocole de la figure (icône
pour créer un nouveau calcul nommé nbsDem contenant comme formule 1. Ce calcul fera partie des objets sources communs à toutes les implémentations. Il faut donc le reclasser. Pour cela utilisez le protocole de la figure (icône  de la barre supérieure).
de la barre supérieure).
Utilisez les flèches de reclassement d’objet ( et
et  ) sur la droite pour que nbsDem se retrouve immédiatement après le calcul p. nbsDem représentera le nombre de succès souhaité.
) sur la droite pour que nbsDem se retrouve immédiatement après le calcul p. nbsDem représentera le nombre de succès souhaité.
De même créez un nouveau calcul nommé nbs avec comme formule 0 et utilisez l’outil Protocole  pour reclasser nbs immédiatement après le calcul ang.
pour reclasser nbs immédiatement après le calcul ang.
Créez un calcul nommé nbs1 contenant comme formule nbs+1 et utilisez l’outil Protocole  pour le reclasser juste après le calcul ang1. nbs1 représente le nombre de succès quand on passe à une branche supérieure.
pour le reclasser juste après le calcul ang1. nbs1 représente le nombre de succès quand on passe à une branche supérieure.
Créez un calcul nommé nbs2 contenant comme formule nbs et utilisez l’outil Protocole  pour le reclasser juste après le calcul ang2. nbs2 représente le nombre de succès quand on passe à une branche inférieure.
pour le reclasser juste après le calcul ang2. nbs2 représente le nombre de succès quand on passe à une branche inférieure.
A l’aide de l’icône utilisez l’outil Protocole  créez les calculs suivants :
créez les calculs suivants :
- Un calcul nommé nbe1 contenant comme formule n1-nbs1
- Un calcul nommé nbe2 contenant comme formule n2-nbs2
- Un calcul nommé pb1 contenant comme formule p^nbs1*q^nbe1
- Un calcul nommé pb2 contenant comme formule p^nbs2*q^nbe2
- Un calcul nommé test1 contenant comme formule nbs1=nbsDem
- Un calcul nommé test2 contenant comme formule nbs2=nbsDem
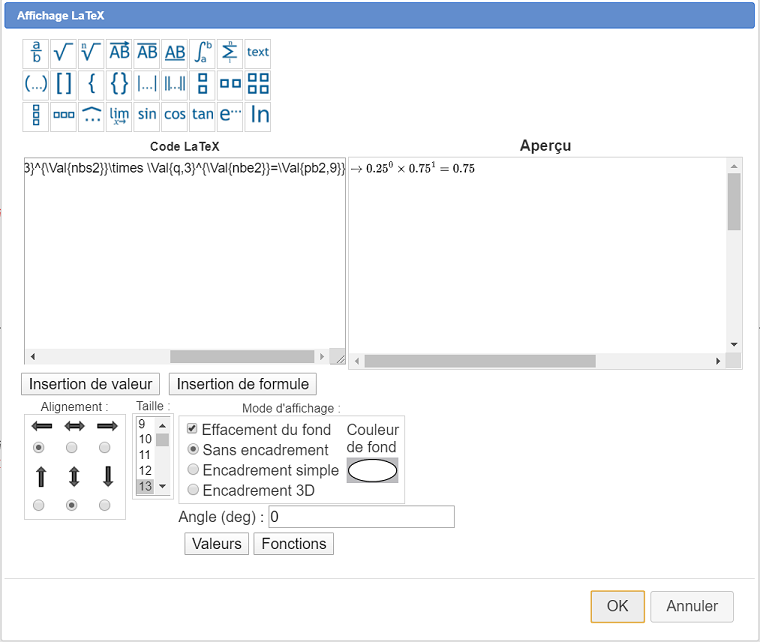
Utilisez maintenant l’icône utilisez l’outil  pour créer un affichage LaTeX lié au point D. Cliquez sur le point D et remplissez la boîte de dialogue comme ci-dessous. N’oubliez pas de bien choisir le mode d’alignement centré horizontalement et avec la flèche gauche pour l’alignement horizontal. Le code LaTeX à entrer est le suivant :
pour créer un affichage LaTeX lié au point D. Cliquez sur le point D et remplissez la boîte de dialogue comme ci-dessous. N’oubliez pas de bien choisir le mode d’alignement centré horizontalement et avec la flèche gauche pour l’alignement horizontal. Le code LaTeX à entrer est le suivant :
\textcolor{\If{test1}{red}{black}}{\rightarrow \Val{p,3}^{\Val{nbs1}}\times \Val{q,3}^{\Val{nbe1}}=\Val{pb1,9}}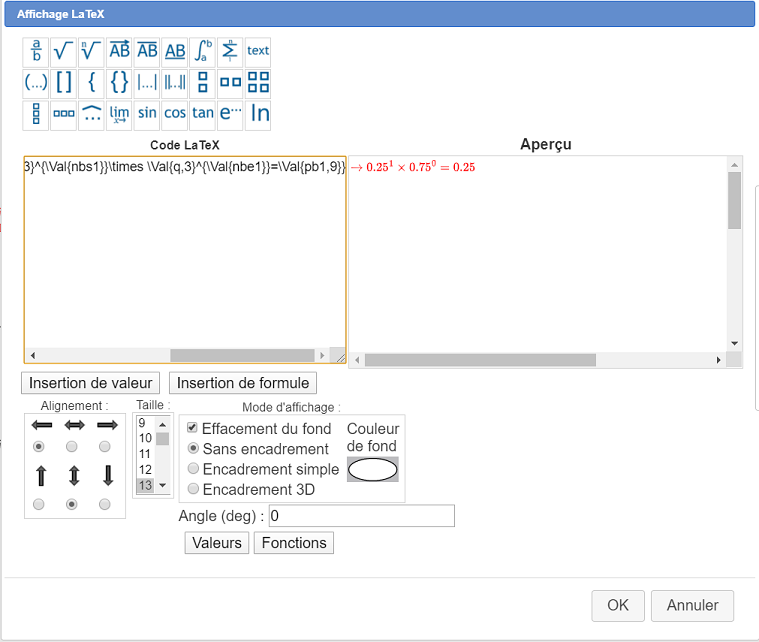
Utilisez maintenant l’icône  pour créer un affichage LaTeX lié au point E. Cliquez sur le point E et remplissez la boîte de dialogue comme ci-dessous. N’oubliez pas de bien choisir le mode d’alignement centré horizontalement et avec la flèche gauche pour l’alignement horizontal. Le code LaTeX à entrer est le suivant :
pour créer un affichage LaTeX lié au point E. Cliquez sur le point E et remplissez la boîte de dialogue comme ci-dessous. N’oubliez pas de bien choisir le mode d’alignement centré horizontalement et avec la flèche gauche pour l’alignement horizontal. Le code LaTeX à entrer est le suivant : \textcolor{\If{test2}{red}{black}}{\rightarrow \Val{p,3}^{\Val{nbs2}}\times \Val{q,3}^{\Val{nbe2}}=\Val{pb2,9}}
Utilisez l’icône  et choisissez l’item Choix des objets sources numériques.
et choisissez l’item Choix des objets sources numériques.
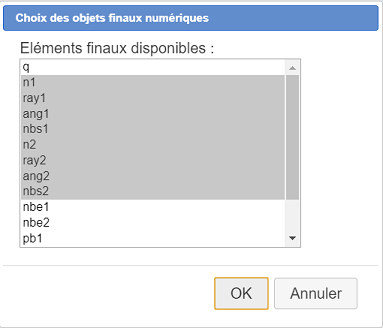
Choisissez comme éléments sources (dans cet ordre ) : coefRay, coefAng, p, nbsDem, n, ray, ang et nbs.
Utilisez de nouveau l’icône  et choisissez l’item Choix des objets sources graphiques.
et choisissez l’item Choix des objets sources graphiques.
Cliquez sur le point A puis cliquez sur le bouton rouge STOP pour indiquer que le choix des objets sources graphiques est terminé.
Utilisez de nouveau l’icône  et choisissez l’item Choix des objets finaux numériques. Sélectionnez les objets finaux numériques comme ci-dessous.
et choisissez l’item Choix des objets finaux numériques. Sélectionnez les objets finaux numériques comme ci-dessous.
Utilisez de nouveau l’icône  et choisissez l’item Choix des objets finaux graphiques. Cliquez sur les points D et E et les deux affichages LaTeX liés à D et E, puis cliquez sur le bouton rouge STOP.
et choisissez l’item Choix des objets finaux graphiques. Cliquez sur les points D et E et les deux affichages LaTeX liés à D et E, puis cliquez sur le bouton rouge STOP.
Utilisez l’icône  pour masquer les points D et E.
pour masquer les points D et E.
Il nous reste à finaliser notre construction.
Utilisez de nouveau l’icône  et choisissez l’item Finir la construction en cours.
et choisissez l’item Finir la construction en cours.
Remplissez la boîte de dialogue comme ci-dessous. Voici le contenu du champ Infos si vous voulez le copier-coller :
#1:Valeur de coefRay (coefficient de réduction à chaque étape pour la longueur des flèches)
#2:Valeur de coefAng (coefficient de réduction à chaque étape pour l'angle des flèches avec l'horizontale)
#3:Valeur de p (probabilité de succès)
#4;Valeur de nbsDem (nombre de succès souhaité)
#5:Valeur de n (le rang de génération de branche)
#6:Le rayon de départ (longueur des flèches)
#7:L'angle de départ en degrés de la première flèche avec l'horizontale
#8:Le nombre de succès (doit être initialisé à zéro)
#9:Le point origine de l'arbre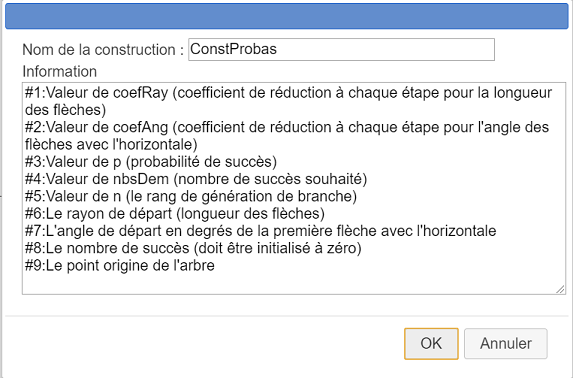
Par sécurité, enregistrez cette figure sous le nom ArbreBinomial2.
Utilisez l’icône  et choisissez l’item Enregistrer une construction de la figure. Enregistrez la construction ConstProbas à l’emplacement de votre choix.
et choisissez l’item Enregistrer une construction de la figure. Enregistrez la construction ConstProbas à l’emplacement de votre choix.
Reprenez la figure ArbreBinomial (qui sera notre figure finale) dans laquelle nous avons déjà créé une macro implémentant la construction ConstArbre.
Utilisez l’icône  et choisissez l’item Incorporer une construction depuis un fichier. Allez chercher la construction ConstProbas à l’endroit où vous l’avez sauvegardée.
et choisissez l’item Incorporer une construction depuis un fichier. Allez chercher la construction ConstProbas à l’endroit où vous l’avez sauvegardée.
Nous allons lui rajouter une macro implémentant la construction ConstProbas.
Déroulez la barre d’outil des affichages et, à sa droite, cliquez sur l’icône  . Choisissez l’item Macro de construction récursive.
. Choisissez l’item Macro de construction récursive.
Cliquez en haut et à gauche de la figure pour désigner l’emplacement de son intitulé.
Remplissez la première boîte de dialogue comme ci-dessous. Prenez garde de bien affecter à chaque niveau de récursion la macro ConstProbas et de bien cocher la case Ne créer que les objets de dernière génération. Lorsque cette construction sera implémentée de façon récursive, les objets finaux autres que ceux servant à implémenter la prochaine génération ne seront pas créés pour les niveaux intermédiaires. Ce n’est que pour le dernière génération que seront implémentés tous les objets finaux. Ainsi les affichages LaTeX contenant les probabilités ne seront implémentés que pour les branches finales de l’arbre.
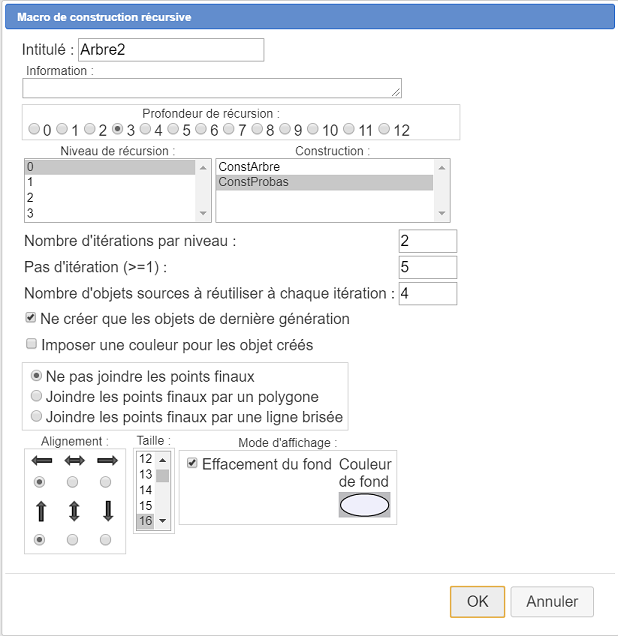
Une nouvelle boîte de dialogue apparaît pour affecter les objets sources numériques.
- Affectez à l’élément n° 1 le calcul coefRay
- Affectez à l’élément n° 2 le calcul coefAng
- Affectez à l’élément n° 3 le calcul p
- Affectez à l’élément n° 4 le calcul nbsDem
- Affectez à l’élément n° 5 le calcul n
- Affectez à l’élément n° 6 le calcul ray
- Affectez à l’élément n° 7 le calcul ang
- Affectez à l’élément n° 8 le calcul nbs
Il vous est maintenant demandé de cliquer sur le point origine de l’arbre. Cliquez sur le même point libre que pour la première macro.
Cliquez sur chacune des deux macros pour l’exécuter. Vous devez voir apparaître l’arbre complet et, au bout des branches finales, les probabilités, en rouge lorsque le nombre de succès est nbsDem (pour l moment égal à 1 et en noir dans les autres cas.
Pour compléter cette figure nous allons créer un curseur qui représentera la nombre de succès demandés.
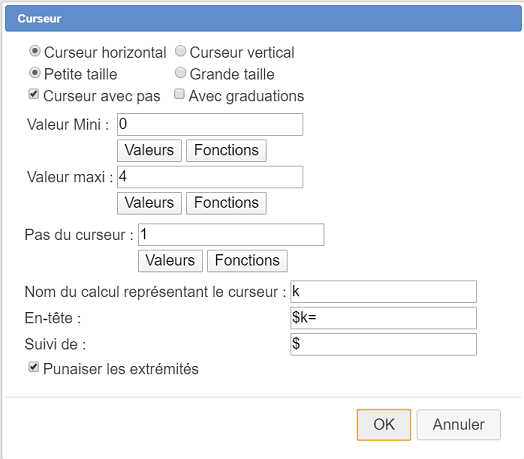
Utilisez l’icône  pour créer un curseur à valeurs entières comme ci-dessous.
pour créer un curseur à valeurs entières comme ci-dessous.
Dans la barre d’outils supérieure, activez l’outil  servant à modifier ou reclasser les objets numériques.
servant à modifier ou reclasser les objets numériques.
Cliquez sur k (qui figure en fin de liste) puis cliquez sur le bouton Reclasser vers le début.
Maintenant nbsDem va pouvoir utiliser la valeur de k.
Cliquez sur nbsDem puis cliquez sur le bouton Modifier. Entrez comme formule k.
Cliquez sur le bouton Fermer pour refermer la boîte de dialogue.
Quand vous capturez le curseur vous voyez les probabilités en bout de branche s’actualiser.
Utilisez l’icône  pour créer :
pour créer :
- un nouveau calcul nommé q contenant comme formule 1-p
- un nouveau calcul nommé coeBin contenant comme formule nCr(4,k)
- un nouveau calcul nommé k’ contenant comme formule 4-k
- un nouveau calcul nommé pk contenant comme formule coebin*p^k*q^k'
Pour finir, nous allons créer un affichage LaTeX donnant la probabilité P(X=k) où X est une variable aléatoire suivant la loi binomiale de paramètres n=4 et p.
Utilisez l’icône  , en haut à droite du curseur en entrez comme code LaTeX :
, en haut à droite du curseur en entrez comme code LaTeX :
P\left( X=k \right)=\left( \begin{array}{l} 4 \\\Val{k} \end{array} \right)\Val{p,3}^\Val{k}\times \left( 1-\Val{p,3} \right)^\Val{k'} = \Val{coebin}\times \Val{p,3}^\Val{k}\times \Val{q,3}^\Val{k'}\approx \Val{pk,9}La figure est finie et vous pouvez utiliser l’outil  pour masquer les deux macros.
pour masquer les deux macros.
Voici ci-dessous la figure finale :