Toutes les versions de cet article : [English] [Español] [Español] [français]
Dans ce deuxième tutoriel sur le calcul matriciel, nous allons créer une figure destinée à résoudre un système de 3 équations à 3 inconnues à coefficients entiers.
Pour cela il vous faut utiliser la version 6.7.3 de MathGraph32 ou une version ultérieure.
Pour vous éviter le plus fastidieux vous allez partir d’une figure déjà préparée et que nous compléterons.
Cliquez dans la barre du haut sur l’icône  et utilisez Figure par code Base 64.
et utilisez Figure par code Base 64.
Utilisez le code Base 64 ci-dessous :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAAAAAAAAQAAABr#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AANhMTEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2ExMgABNQAAAAFAFAAAAAAAAAAAAAIA#####wADYTEzAAEzAAAAAUAIAAAAAAAAAAAAAgD#####AANhMjEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2EyMgABMQAAAAE#8AAAAAAAAAAAAAIA#####wADYTIzAAEzAAAAAUAIAAAAAAAAAAAAAgD#####AANhMzEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2EzMgABMQAAAAE#8AAAAAAAAAAAAAIA#####wADYTMzAAEyAAAAAUAAAAAAAAAAAAAAAgD#####AAJiMQABMQAAAAE#8AAAAAAAAAAAAAIA#####wACYjIAATIAAAABQAAAAAAAAAAAAAACAP####8AAmIzAAEzAAAAAUAIAAAAAAAA#####wAAAAQAD0NFZGl0ZXVyRm9ybXVsZQD#####AAAAAAEAAP####8OQEdAAAAAAABAOYUeuFHrhgAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAABAAkkYV97MTF9PSQAAAAEAAEAAT0BAQAAAAMA#####wAAAAABAAD#####DkBn8AAAAAAAQDmFHrhR64YAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAAAgAJJGFfezEyfT0kAAAABAABAAE9AQEAAAADAP####8AAAAAAQAA#####w5AdVgAAAAAAEA3hR64UeuGAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAMACSRhX3sxM309JAAAAAQAAQABPQEBAAAAAwD#####AAAAAAEAAP####8OQEdAAAAAAABAUWFHrhR64gAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAEAAkkYV97MjF9PSQAAAAEAAEAAT0BAQAAAAMA#####wAAAAABAAD#####DkBn8AAAAAAAQFFhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAABQAJJGFfezIyfT0kAAAABAABAAE9AQEAAAADAP####8AAAAAAQAA#####w5AdVgAAAAAAEBQYUeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAYACSRhX3syM309JAAAAAQAAQABPQEBAAAAAwD#####AAAAAAEAAP####8OQEdAAAAAAABAXGFHrhR64gAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAHAAkkYV97MzF9PSQAAAAEAAEAAT0BAQAAAAMA#####wAAAAABAAD#####DkBn0AAAAAAAQFvhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAACAAJJGFfezMyfT0kAAAABAABAAE9AQEAAAADAP####8AAAAAAQAA#####w5AdUgAAAAAAEBa4UeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAkACSRhX3szM309JAAAAAQAAQABPQEBAAAAAwD#####AAAAAAEAAP####8OQH6oAAAAAABAOIUeuFHrhgAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAKAAYkYl8xPSQAAAAEAAEAAT0BAQAAAAMA#####wAAAAABAAD#####DkB+mAAAAAAAQFAhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAACwAGJGJfMj0kAAAABAABAAE9AQEAAAADAP####8AAAAAAQAA#####w5AfpgAAAAAAEBaIUeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAwABiRiXzM9JAAAAAQAAQABPQEB#####wAAAAIADENDb21tZW50YWlyZQD#####AP8AAAEAAP####8QQDOAAAAAAABAeKhR64UeuAAAAAAAAAAAAAAAAAABAAAAAAAAAAAA8E4nZW50cmV6IGNvbW1lIGNvZWZmaWNpZW50cyBxdWUgZGVzIG5vbWJyZXMgZW50aWVycy4KTGEgc29sdXRpb24gc2VyYSBlbmNvcmUgYm9ubmUgc2kgbGVzIGNvZWZmaWNpZW50cwpzb250IGRlcyBub21icmVzIHJhdGlvbm5lbHMgbWFpcyBsJ2FmZmljaGFnZQpkdSBzeXN0w6htZSBzZXJhIGFwcHJvY2jDqSAobWFpcyDDoCBjb25kaXRpb24gcXVlCmxlcyBjb2VmZmljaWVudHMgcmVzdGVudCBhc3NleiAic2ltcGxlcyIpLv###############w==Dans cette figure ont été créés les calculs $a_{11},a_{12},a_{13},a_{21},a_{22},a_{23},a_{31},a_{32},a_{33}$ qui sont les coefficients du système et les calculs $b_1,b_2,b_3$ qui sont les termes constants de droite.
Cette figure contient aussi des éditeurs de formules associés à tous ces coefficients.
Nous désirons maintenant afficher le système à résoudre dans un affichage LaTeX.
Pour cela nous allons créer trois fonctions réelles de 3 variables.
Déroulez la barre d’outils des calculs et cliquez à droite sur l’icône  .
.
Dans la liste, choisissez Fonction réelle de trois variables et remplissez la boîte de dialogue comme ci-dessous.
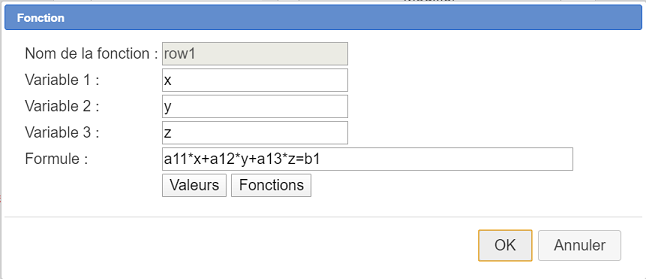
Voici ci-dessous la formule à entrer pour la fonction row1 :
a11*x+a12*y+a13*z=b1
Procédez de même pour créer une fonction de 3 variables nommée row2 avec comme formule :
a21*x+a22*y+a23*z=b2
Et une fonction de 3 variables nommée row3 avec comme formule :
a31*x+a32*y+a33*z=b3
Maintenant nous allons créer un affichage LaTeX pour afficher le système.
Déroulez la barre d’outils des affichages et cliquez sur l’icône 
Cliquez sous les éditeurs de formule à gauche de la figure et utilisez le code LaTeX ci-dessous (vous pouvez utiliser le bouton  et cliquer sur le bouton Insertion de formule).
et cliquer sur le bouton Insertion de formule).
Code LaTeX :
\text{Système : }
\left\{ \begin{array}{l}
\ForSimp{row1}
\\ \ForSimp{row2}
\\ \ForSimp{row3}
\end{array} \right.Maintenant nous allons créer une matrice A dont les termes seront les coefficients du système.
Déroulez la barre d’outils des calculs et cliquez à droite sur l’icône  .
.
Dans la liste, choisissez Matrice et remplissez la boîte de dialogue comme ci-dessous pour créer la matrice A.

De nouveau créez une matrice B comme ci-dessous :
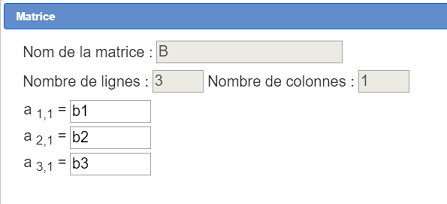
Le système à résoudre est donc A \times X = B où X est la matrice inconnue.
Pour savoir si ce système admet une solution unique nous allons calculer le déterminant de la matrice A.
Déroulez la barre d’outils des calculs et cliquez à droite sur l’icône  .
.
Dans la liste, choisissez Déterminant et remplissez la boîte de dialogue comme ci-dessous (le nom choisi est detA).
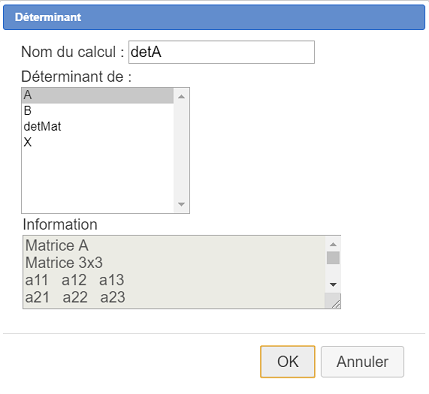
Dans la barre d’outils des calculs, utilisez l’icône  pour créer un calcul réel nommé detnul avec comme formule :
pour créer un calcul réel nommé detnul avec comme formule :
detA=0
Créons maintenant un calcul matriciel nommé X contenant la solution du système quand elle existe et est unique.
Déroulez la barre d’outils des calculs et cliquez à droite sur l’icône  .
.
Dans la liste, choisissez Calcul matriciel et remplissez la boîte de dialogue comme ci-dessous.
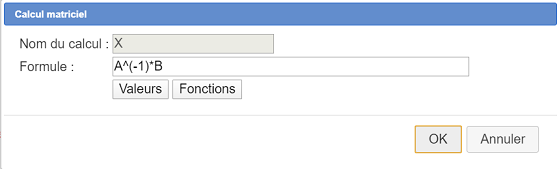
Le nom du calcul matriciel est X formule à entrer est la suivante :
A^(-1)*B
A^(-1) représente la matrice inverse de A (si celle-ci est inversible).
Il nous reste à créer un affichage LaTeX pour afficher la solution.
Cet affichage LaTeX contiendra un affichage conditionnel suivant que detnul vaut 1 (une seule solution) ou non.
Déroulez la barre d’outils des affichages et cliquez sur l’icône  .
.
Cliquez sous l’affichage LaTeX précédent affichant le système et utilisez le code LaTeX suivant :
\If{detnul}
{
\text{Le système n'a pas un seul triplet solution}
}
{
\begin{array}{l}
\text{Le système a un seul triplet solution}
\\ \left( \begin{array}{l}
x
\\ y
\\ z
\end{array} \right)
= \left( \ValFrac{X} \right)
\end{array}
}A remarquer : Cet affichage LaTeX utilise un code LaTeX spécifique à MathGraph32 \ValFrac.
Ce code affiche la matrice A avec chaque terme remplacé par son approximation rationnelle à 10^(-12) près. Ainsi, si les coefficients ne sont pad trop grands, la solution affichée sera exacte.
Voici le code Base 64 de la figure finale :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAAAAAAAAQAAACb#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AANhMTEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2ExMgABNQAAAAFAFAAAAAAAAAAAAAIA#####wADYTEzAAEzAAAAAUAIAAAAAAAAAAAAAgD#####AANhMjEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2EyMgABMQAAAAE#8AAAAAAAAAAAAAIA#####wADYTIzAAEzAAAAAUAIAAAAAAAAAAAAAgD#####AANhMzEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2EzMgABMQAAAAE#8AAAAAAAAAAAAAIA#####wADYTMzAAEyAAAAAUAAAAAAAAAAAAAAAgD#####AAJiMQABMQAAAAE#8AAAAAAAAAAAAAIA#####wACYjIAATIAAAABQAAAAAAAAAAAAAACAP####8AAmIzAAEzAAAAAUAIAAAAAAAA#####wAAAAEACUNGb25jTlZhcgD#####AARyb3cxABRhMTEqeCthMTIqeSthMTMqej1iMf####8AAAABAApDT3BlcmF0aW9uCAAAAAQAAAAABAAAAAAEAv####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAAB#####wAAAAIAEUNWYXJpYWJsZUZvcm1lbGxlAAAAAAAAAAQCAAAABQAAAAIAAAAGAAAAAQAAAAQCAAAABQAAAAMAAAAGAAAAAgAAAAUAAAAKAAAAAwABeAABeQABegAAAAMA#####wAEcm93MgAUYTIxKngrYTIyKnkrYTIzKno9YjIAAAAECAAAAAQAAAAABAAAAAAEAgAAAAUAAAAEAAAABgAAAAAAAAAEAgAAAAUAAAAFAAAABgAAAAEAAAAEAgAAAAUAAAAGAAAABgAAAAIAAAAFAAAACwAAAAMAAXgAAXkAAXoAAAADAP####8ABHJvdzMAFGEzMSp4K2EzMip5K2EzMyp6PWIzAAAABAgAAAAEAAAAAAQAAAAABAIAAAAFAAAABwAAAAYAAAAAAAAABAIAAAAFAAAACAAAAAYAAAABAAAABAIAAAAFAAAACQAAAAYAAAACAAAABQAAAAwAAAADAAF4AAF5AAF6#####wAAAAQAD0NFZGl0ZXVyRm9ybXVsZQD#####AAAAAAEAAP####8OQEdAAAAAAABAOYUeuFHrhgAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAABAAkkYV97MTF9PSQAAAAEAAEAAT0BAQAAAAcA#####wAAAAABAAD#####DkBn8AAAAAAAQDmFHrhR64YAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAAAgAJJGFfezEyfT0kAAAABAABAAE9AQEAAAAHAP####8AAAAAAQAA#####w5AdVgAAAAAAEA3hR64UeuGAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAMACSRhX3sxM309JAAAAAQAAQABPQEBAAAABwD#####AAAAAAEAAP####8OQEdAAAAAAABAUWFHrhR64gAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAEAAkkYV97MjF9PSQAAAAEAAEAAT0BAQAAAAcA#####wAAAAABAAD#####DkBn8AAAAAAAQFFhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAABQAJJGFfezIyfT0kAAAABAABAAE9AQEAAAAHAP####8AAAAAAQAA#####w5AdVgAAAAAAEBQYUeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAYACSRhX3syM309JAAAAAQAAQABPQEBAAAABwD#####AAAAAAEAAP####8OQEdAAAAAAABAXGFHrhR64gAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAHAAkkYV97MzF9PSQAAAAEAAEAAT0BAQAAAAcA#####wAAAAABAAD#####DkBn0AAAAAAAQFvhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAACAAJJGFfezMyfT0kAAAABAABAAE9AQEAAAAHAP####8AAAAAAQAA#####w5AdUgAAAAAAEBa4UeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAkACSRhX3szM309JAAAAAQAAQABPQEBAAAABwD#####AAAAAAEAAP####8OQH6oAAAAAABAOIUeuFHrhgAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAKAAYkYl8xPSQAAAAEAAEAAT0BAQAAAAcA#####wAAAAABAAD#####DkB+mAAAAAAAQFAhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAACwAGJGJfMj0kAAAABAABAAE9AQEAAAAHAP####8AAAAAAQAA#####w5AfpgAAAAAAEBaIUeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAwABiRiXzM9JAAAAAQAAQABPQEB#####wAAAAIABkNMYXRleAD#####AAAAAAEAAP####8QQC0AAAAAAABAY#Cj1wo9cQAAAAAAAAAAAAAAAAABAAAAAAAAAAAAc1x0ZXh0e1N5c3TDqG1lIDogfQpcbGVmdFx7IFxiZWdpbnthcnJheX17bH0KXEZvclNpbXB7cm93MX0gClxcIFxGb3JTaW1we3JvdzJ9ClxcIFxGb3JTaW1we3JvdzN9ClxlbmR7YXJyYXl9IFxyaWdodC7#####AAAAAQAIQ01hdHJpY2UA#####wABQQAAAAMAAAADAAAABQAAAAEAAAAFAAAAAgAAAAUAAAADAAAABQAAAAQAAAAFAAAABQAAAAUAAAAGAAAABQAAAAcAAAAFAAAACAAAAAUAAAAJAAAACQD#####AAFCAAAAAwAAAAEAAAAFAAAACgAAAAUAAAALAAAABQAAAAz#####AAAAAQAUQ0ltcGxlbWVudGF0aW9uUHJvdG8A#####wAMRMOpdGVybWluYW50AAAAAQAAAAEAAAABAAAAHf####8AAAABAAhDQ2FsY01hdAAAAAAfAAZkZXRNYXQACGRldGVyKEEp#####wAAAAIACUNGb25jdGlvbhcAAAAFAAAAHQAAAAIBAAAAHwAEZGV0QQALZGV0TWF0KDEsMSn#####AAAAAQAIQ1Rlcm1NYXQAAAAgAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAAAAAAAgD#####AAZkZXRudWwABmRldEE9MAAAAAQIAAAABQAAACEAAAABAAAAAAAAAAAAAAALAP####8AAVgACEFeKC0xKSpCAAAABAL#####AAAAAQAKQ1B1aXNzYW5jZQAAAAUAAAAd#####wAAAAEADENNb2luc1VuYWlyZQAAAAE#8AAAAAAAAAAAAAUAAAAeAAAACAD#####AAAAAAEAAP####8QQCkAAAAAAABAcShR64UeuAAAAAAAAAAAAAAAAAABAAAAAAAAAAAA7FxJZntkZXRudWx9CnsKXHRleHR7TGUgc3lzdMOobWUgbidhIHBhcyB1biBzZXVsIHRyaXBsZXQgc29sdXRpb259Cn0KewpcYmVnaW57YXJyYXl9e2x9Clx0ZXh0e0xlIHN5c3TDqG1lIGEgdW4gc2V1bCB0cmlwbGV0IHNvbHV0aW9ufQpcXCBcbGVmdCggXGJlZ2lue2FycmF5fXtsfQp4IApcXCB5ClxcIHoKXGVuZHthcnJheX0gXHJpZ2h0KQo9ICBcbGVmdCggXFZhbEZyYWN7WH0gXHJpZ2h0KQpcZW5ke2FycmF5fQp9#####wAAAAIADENDb21tZW50YWlyZQD#####AP8AAAEAAP####8QQDOAAAAAAABAeKhR64UeuAAAAAAAAAAAAAAAAAABAAAAAAAAAAAA8E4nZW50cmV6IGNvbW1lIGNvZWZmaWNpZW50cyBxdWUgZGVzIG5vbWJyZXMgZW50aWVycy4KTGEgc29sdXRpb24gc2VyYSBlbmNvcmUgYm9ubmUgc2kgbGVzIGNvZWZmaWNpZW50cwpzb250IGRlcyBub21icmVzIHJhdGlvbm5lbHMgbWFpcyBsJ2FmZmljaGFnZQpkdSBzeXN0w6htZSBzZXJhIGFwcHJvY2jDqSAobWFpcyDDoCBjb25kaXRpb24gcXVlCmxlcyBjb2VmZmljaWVudHMgcmVzdGVudCBhc3NleiAic2ltcGxlcyIpLv###############w==Vous pouvez voir la figure finale ci-dessous.