Toutes les versions de cet article : [English] [Español] [français]
En este tercer tutorial de cálculo matricial, usaremos una macro-construcción y una macro de construcción recursiva para crear un fractal denominado Helecho de Barnsley.
Podemos referirnos a esto artículo Wikipedia.
Iniciemos MathGraph32 (versión 6.7.3 o posterior) y usemos el icono  para crear una figura con un referencial. Elijamos un sistema de coordenadas ortogonales sin cuadrícula y sin graduación.
para crear una figura con un referencial. Elijamos un sistema de coordenadas ortogonales sin cuadrícula y sin graduación.
Utilicemos el icono  para crear tres cálculos reales p1, p2 y p3 con las fórmulas siguientes :
para crear tres cálculos reales p1, p2 y p3 con las fórmulas siguientes :
| Nombre del cálculo | Fórmula |
| p1 | 0.01 |
| p2 | 0.85 |
| p3 | 0.07 |
Es inútil definir un cálculo p4 porque la suma de las 4 probabilidades es igual a 1.
Simularemos una tirada aleatoria eligiendo un número aleatorio entre 0 y 1 (1 excluido).
Creemos los siguientes dos cálculos reales :
| Nombre del cálculo | Fórmula | Comentario |
| alea | rand(0) | Número aleatorio de [0 ;1[ |
| caso | si(alea<p1,1,si(alea<p1+p2,2,si(alea<p1+p2+p3,3,4))) | caso es 1, 2, 3 o 4 dependiendo de la resultado obtenido en alea |
Ahora vamos a definir 8 matrices por sus elementos.
Para hacer esto, bajemos la barra de cálculos y hagamos clic en el ícono  que nos permitirá usar herramientas de uso menos común.
que nos permitirá usar herramientas de uso menos común.
En la lista propuesta, elegimos Matriz.
Tendremos que, para cada matriz, definir su número de filas y columnas y luego dar cada uno de sus elementos.
| Nombre de la matriz | Número de filas | Número de columnas | Elementos |
| A1 | 2 | 2 | $\begin{matrix}0 & 0\\ 0 & 0.16\end{matrix}$ |
| A2 | 2 | 2 | $\begin{matrix}0.85 & 0.04\\ -0.04 & 0.85\end{matrix}$ |
| A3 | 2 | 2 | $\begin{matrix}0.2 & -0.26\\ 0.23 & 0.22\end{matrix}$ |
| A4 | 2 | 2 | $\begin{matrix}-0.15 & 0.28\\ 0.26 & 0.24\end{matrix}$ |
| B1 | 2 | 1 | $\begin{matrix}0 \\ 0 \end{matrix}$ |
| B2 | 2 | 1 | $\begin{matrix}0 \\ 1.6 \end{matrix}$ |
| B3 | 2 | 1 | $\begin{matrix}0 \\ 1.6 \end{matrix}$ |
| B4 | 2 | 1 | $\begin{matrix}0 \\ 0.44 \end{matrix}$ |
Ahora vamos a definir dos matrices A (dos filas y dos columnas) y B (dos filas y una columna).
Para hacer esto, volvemos a bajar la barra de cálculos y hacemos clic en el icono  .
.
En la lista propuesta, elegimos Cálculo matricial.
Definamos A y B como se muestra a continuación :
| Nombre de la matriz | Fórmula |
| A | si(caso=1,A1,si(caso=2,A2,si(caso=3,A3,A4))) |
| B | si(caso=1,B1,si(caso=2,B2,si(caso=3,B3,B4))) |
Desplegamos nuevamente la barra de cálculos y hacemos clic en el icono  .
.
En la lista propuesta, elegimos Matriz.
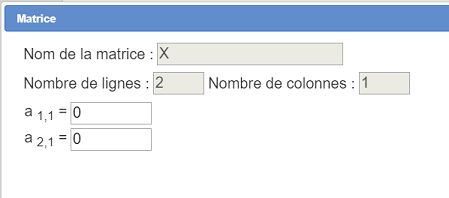
Creamos la matriz X como se muestra a continuación (sus dos elementos son nulos) :
Usando el ícono  creamos un nuevo cálculo real llamado alea ’ con la siguiente fórmula :
creamos un nuevo cálculo real llamado alea ’ con la siguiente fórmula :
rand(0)+alea*0
Explicaremos por qué esta fórmula en lugar de rand (0) más adelante.
Ahora creamos un nuevo cálculo matricial llamado Y con la siguiente fórmula :
A*X+B
Nos queda crear un punto cuyas coordenadas en nuestro referencial sean los elementos de la matriz Y.
En la paleta de colores, activemos el color rojo, bajemos la barra de iconos de puntos y hagamos clic en el icono  (creación de un punto por sus coordenadas en un referencial).
(creación de un punto por sus coordenadas en un referencial).
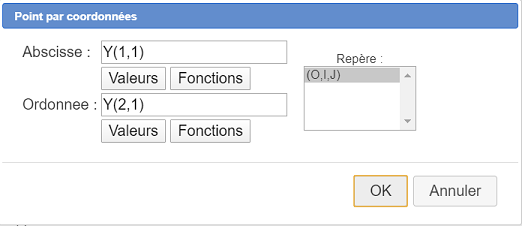
Complete el cuadro de diálogo como se muestra a continuación :
Ahora vamos a crear una macro-construcción cuyos elementos fuente serán los siguientes objetos :
| El sistema de coordenadas (0 ; I, J) |
| El cálculo p1 |
| El cálculo p2 |
| El cálculo p3 |
| La matriz A1 |
| La matriz A2 |
| La matriz A3 |
| La matriz A4 |
| La matriz B1 |
| La matriz B2 |
| La matriz B3 |
| La matriz B4 |
| El cálculo alea |
| La matriz X |
Los objetos finales serán los siguientes :
| El cálculo alea ’ |
| La matriz Y |
| El punto con coordenadas (y(1,1), Y(2,1) |
Para que una construcción sea válida, los objetos finales deben depender de al menos un objeto fuente. Esta es la razón por la que en la fórmula de alea ’ ponemos como fórmula rand(0)+alea*0 para que este cálculo dependa del objeto fuente alea.
Una vez creada esta macro-construcción, crearemos una macro de construcción iterativa que, en cada etapa, sustituirá el cálculo alea por el cálculo alea’ y la matriz X por la matriz Y. La nube de puntos resultante representará nuestro helecho.
Así que comencemos creando nuestra macro-construcción.
Para realizar esto, hacemos clic en en la barra de herramientas superior en el icono ![]() que muestra herramientas adicionales.
que muestra herramientas adicionales.
Luego hacemos clic en el icono  luego elegimos Elección de objetos fuente numéricos.
luego elegimos Elección de objetos fuente numéricos.
Se abre un cuadro de diálogo.
Para seleccionar un objeto de fuente numérico, seleccionamos un objeto en la lista de la izquierda y luego hacemos clic en el botón Insertar o hacemos doble clic en un elemento de la lista de la izquierda.
Deberíamos tener los siguientes elementos en la lista de la derecha (en ese orden) :
| (0 ; I,J) |
| p1 |
| p2 |
| p3 |
| A1 |
| A2 |
| A3 |
| A4 |
| B1 |
| B2 |
| B3 |
| B4 |
| alea |
| X |
Advertencia : Es importante no agregar alea hasta que hayan agregado las matrices de A1 a B4.
Validemos nuestro cuadro de diálogo.
Nuestra macro-construcción no tiene objetos fuente gráficos.
Ahora elijamos los objetos finales numéricos.
Hacemos clic en el icono  pluego elegimos Elección de objetos finales numéricos.
pluego elegimos Elección de objetos finales numéricos.
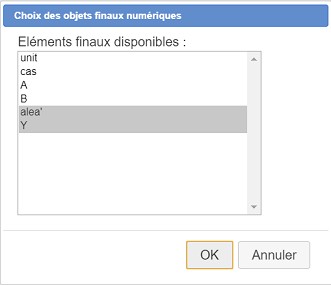
En la lista de la izquierda, hacemos clic en alea ’ y en Y para seleccionarlos como se muestra a continuación y luego validamos.
Nos queda designar nuestro objeto final gráfico, que es el último punto rojo que hemos creado.
Hacemos clic en el icono  luego elegimos Elección de los objetos gráficos finales.
luego elegimos Elección de los objetos gráficos finales.
Hacemos clic en el punto rojo y luego hacemos clic en la parte inferior derecha del botón rojo DETENER.
Antes de finalizar nuestra construcción, le daremos a nuestro punto rojo un estilo de "píxel".
En la paleta de estilos de puntos, elegimos el estilo de puntos de píxeles (parte inferior izquierda), hacemos clic en en la barra superior de la herramienta Paleta  y cliqueamos sobre el punto rojo.
y cliqueamos sobre el punto rojo.
Todavía tenemos que finalizar nuestra construcción.
Cliqueamos sobre el icono  luego elegimos Finalizar construcción actual.
luego elegimos Finalizar construcción actual.
Se abre un cuadro de diálogo.
En el campo Nombre de la construcción ingrese por ejemplo Barnsley.
En el campo Información, ingrese lo siguiente :
#1:El referencial
#2:Probabilidad del caso 1
#3:Probabilidad del caso 2
#4:Probabilidad del caso 3
#5:Matriz A para el caso 1
#6:Matriz A para el caso 2
#7:Matriz A para el caso 3
#8:Matriz A para el caso 4
#9:Matriz B para el caso 1
#10:Matriz B para el caso 2
#11:Matriz B para el caso 3
#12:Matriz B para el caso 4
#13:Cálculo que proporciona un número aleatorio entre 0 y 1
#14:Valor inicial de la matriz XLo que ponemos en el campo de información se usa para dar una pista a un usuario de nuestra macro para cada objeto fuente.
Validamos. Se crea nuestra construcción.
Si quisiéramos utilizar esta construcción en otra figura, solo tendríamos que hacer clic en el icono  luego elegir Guardar una construcción de la figura en un archivo. Nuestra construcción luego se guardaría en un archivo con un sufijo mgc.
luego elegir Guardar una construcción de la figura en un archivo. Nuestra construcción luego se guardaría en un archivo con un sufijo mgc.
Ahora vamos a crear una macro de construcción iterativa que utilizará la macro construcción que acabamos de crear.
Para hacer esto, bajamos la barra de herramientas de visualización y hacemos clic en el icono ![]() que luego nos ofrece diferentes tipos de macros que podemos crear.
que luego nos ofrece diferentes tipos de macros que podemos crear.
Como nuestra figura incluye una macro-construcción, entre las herramientas propuestas se encuentra la opción Macro de construcción iterativa.
Primero hagamos clic donde se mostrará el título de la macro, en la parte superior izquierda de nuestra figura.
Se abre un cuadro de diálogo.
Llene este cuadro como se muestra a continuación :
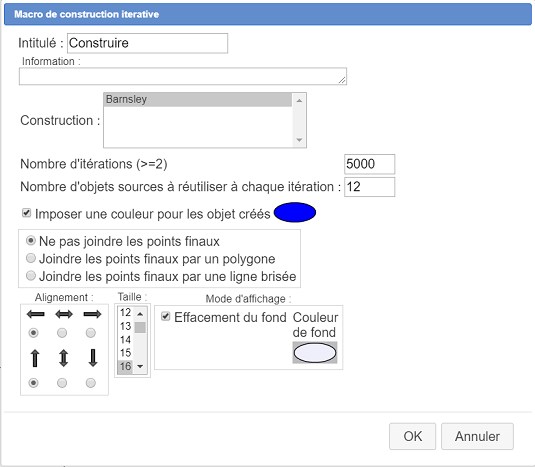
Una vez validado, se abre otro cuadro de diálogo que nos permite elegir los objetos fuente. A cada uno de los 14 elementos fuente se le debe asignar un objeto de la figura.
Por ejemplo, a continuación, se acaba de asignar al cuarto elemento fuente la probabilidad contenida en el cálculo p3.
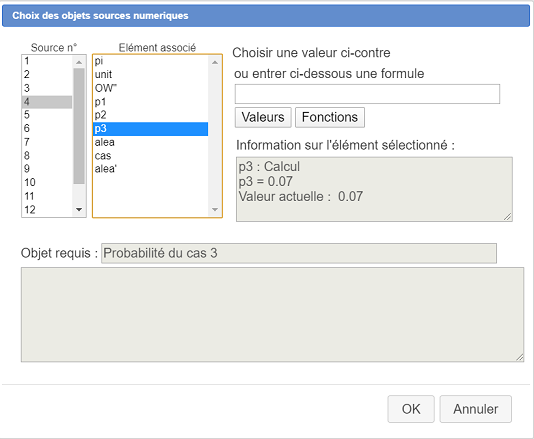
Aquí están las asignaciones a realizar :
| Elemento fuente nº | Elemento a asignar |
| 1 | (O ;i,j) |
| 2 | p1 |
| 3 | p2 |
| 4 | p3 |
| 5 | A1 |
| 6 | A2 |
| 7 | A3 |
| 8 | A4 |
| 9 | B1 |
| 10 | B2 |
| 11 | B3 |
| 12 | B4 |
| 13 | alea |
| 14 | X |
Luego validemos nuestro cuadro de diálogo.
Nuestra macro Construir ahora es visible en la parte superior izquierda de la figura.
Tengamos en cuenta que los primeros 12 elementos fuente son comunes a todas las implementaciones sucesivas de la macro-construcción.
Por lo tanto, cada nueva iteración toma estos elementos comunes como los primeros 12 elementos fuente, siendo el 13-ésimo el primer objeto final de la implementación anterior de la construcción (alea ’) y el 14 el segundo elemento final, es decir, la matriz Y.
En este punto, es prudente guardar nuestra figura en la ubicación que elija porque, una vez que se haya ejecutado la macro de compilación, la figura contendrá una gran cantidad de objetos y proporcionará un archivo muy grande si lo guarda.
En la barra de herramientas superior, ahora podemos activar la herramienta  y luego hacer clic en Construir.
y luego hacer clic en Construir.
Pasados unos segundos (dependiendo de la potencia de la máquina) veremos aparecer nuestro helecho Barnsley.
A continuación se muestra el código Base 64 de la figura resultante seguido de la figura en línea.
Código base 64 :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAABAAAABgAIQmFybnNsZXkBkSMxOkxlIHJlcMOocmUKIzI6UHJvYmFiaWxpdMOpIGR1IGNhcyAxCiMzOlByb2JhYmlsaXTDqSBkdSBjYXMgMgojNDpQcm9iYWJpbGl0w6kgZHUgY2FzIDMKIzU6TWF0cmljZSBBIHBvdXIgbGUgY2FzIDEKIzY6TWF0cmljZSBBIHBvdXIgbGUgY2FzIDIKIzc6TWF0cmljZSBBIHBvdXIgbGUgY2FzIDMKIzg6TWF0cmljZSBBIHBvdXIgbGUgY2FzIDQKIzk6TWF0cmljZSBCIHBvdXIgbGUgY2FzIDEKIzEwOk1hdHJpY2UgQiBwb3VyIGxlIGNhcyAyCiMxMTpNYXRyaWNlIEIgcG91ciBsZSBjYXMgMwojMTI6TWF0cmljZSBCIHBvdXIgbGUgY2FzIDQKIzEzOkNhbGN1bCBmb3Vybmlzc2FudCB1biBub21icmUgYWzDqWF0b2lyZSBlbnRyZSAwIGV0IDEKIzE0OlZhbGV1ciBpbml0aWFsZSBkZSBsYSBtYXRyaWNlIFgKAAAADgAAAAMCAAAAFP####8AAAABABFDRWxlbWVudEdlbmVyaXF1ZQAAAAAAGgAAABoAAAAAAAJwMf####8AAAABAAAAAAACcDL#####AAAAAQAAAAAAAnAz#####wAAAAEAAAAAAAJBMf####8AAAAfAAAAAAACQTL#####AAAAHwAAAAAAAkEz#####wAAAB8AAAAAAAJBNP####8AAAAfAAAAAAACQjH#####AAAAHwAAAAAAAkIy#####wAAAB8AAAAAAAJCM#####8AAAAfAAAAAAACQjT#####AAAAHwAAAAAABGFsZWH#####AAAAAQAAAAAAAVj#####AAAAH#####8AAAABAAdDQ2FsY3VsAP####8AA2NhcwA0c2koYWxlYTxwMSwxLHNpKGFsZWE8cDErcDIsMixzaShhbGVhPHAxK3AyK3AzLDMsNCkpKf####8AAAABAA1DRm9uY3Rpb24zVmFyAP####8AAAABAApDT3BlcmF0aW9uBP####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAAMAAAABAAAAAH#####AAAAAQAKQ0NvbnN0YW50ZT#wAAAAAAAAAAAAAgAAAAADBAAAAAQAAAAMAAAAAwAAAAAEAAAAAQAAAAQAAAACAAAABUAAAAAAAAAAAAAAAgAAAAADBAAAAAQAAAAMAAAAAwAAAAADAAAAAAQAAAABAAAABAAAAAIAAAAEAAAAAwAAAAVACAAAAAAAAAAAAAVAEAAAAAAAAP####8AAAABAAhDQ2FsY01hdAD#####AAFBAClzaShjYXM9MSxBMSxzaShjYXM9MixBMixzaShjYXM9MyxBMyxBNCkpKQAAAAIAAAAAAwgAAAAEAAAADgAAAAU#8AAAAAAAAAAAAAQAAAAEAAAAAgAAAAADCAAAAAQAAAAOAAAABUAAAAAAAAAAAAAABAAAAAUAAAACAAAAAAMIAAAABAAAAA4AAAAFQAgAAAAAAAAAAAAEAAAABgAAAAQAAAAHAAAABgD#####AAFCAClzaShjYXM9MSxCMSxzaShjYXM9MixCMixzaShjYXM9MyxCMyxCNCkpKQAAAAIAAAAAAwgAAAAEAAAADgAAAAU#8AAAAAAAAAAAAAQAAAAIAAAAAgAAAAADCAAAAAQAAAAOAAAABUAAAAAAAAAAAAAABAAAAAkAAAACAAAAAAMIAAAABAAAAA4AAAAFQAgAAAAAAAAAAAAEAAAACgAAAAQAAAALAAAAAQH#####AAVhbGVhJwAOcmFuZCgwKSthbGVhKjAAAAADAP####8AAAACAAlDRm9uY3Rpb24RAAAABQAAAAAAAAAAP+rYUPYavTYAAAADAgAAAAQAAAAMAAAABQAAAAAAAAAAAAAABgH#####AAFZAAVBKlgrQgAAAAMAAAAAAwIAAAAEAAAADwAAAAQAAAANAAAABAAAABD#####AAAAAQAQQ1BvaW50RGFuc1JlcGVyZQH#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABwAAAAAA#####wAAAAEACENUZXJtTWF0AAAAEgAAAAU#8AAAAAAAAAAAAAU#8AAAAAAAAAAAAAkAAAASAAAABUAAAAAAAAAAAAAABT#wAAAAAAAAAAAAAQAAACP#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0NgAAAAVACSH7VEQtGP####8AAAABAApDUG9pbnRCYXNlAP####8AAAAAAA4AAU8AwCgAAAAAAAAAAAAAAAAAAAAABQABQHuAAAAAAABAf9AAAAAAAP####8AAAABABRDRHJvaXRlRGlyZWN0aW9uRml4ZQD#####AQAAAAAQAAABAAAAAQAAAAEBP#AAAAAAAAD#####AAAAAQAPQ1BvaW50TGllRHJvaXRlAP####8AAAAAAA4AAUkAwBgAAAAAAAAAAAAAAAAAAAAABQABQEgAAAAAAAAAAAAC#####wAAAAEACUNEcm9pdGVBQgD#####AAAAAAAQAAABAAAAAQAAAAEAAAAD#####wAAAAEAFkNEcm9pdGVQZXJwZW5kaWN1bGFpcmUA#####wAAAAAAEAAAAQAAAAEAAAABAAAABP####8AAAABAAlDQ2VyY2xlT0EA#####wEAAAAAAAABAAAAAQAAAAP#####AAAAAQAQQ0ludERyb2l0ZUNlcmNsZQD#####AAAABQAAAAb#####AAAAAQAQQ1BvaW50TGllQmlwb2ludAD#####AQAAAAAQAAABAAAFAAEAAAAHAAAAEgD#####AAAAAAAOAAFKAMAoAAAAAAAAwBAAAAAAAAAAAAUAAgAAAAf#####AAAAAgAHQ1JlcGVyZQD#####AObm5gAAAAEAAAABAAAAAwAAAAkAAAAAAAAFAAAAAAAAAAAAAAAFAAAAAAAAAAAAAAAFP#AAAAAAAAAAAAAFP#AAAAAAAAD#####AAAAAQAKQ1VuaXRleFJlcAD#####AAR1bml0AAAACv####8AAAABAAtDSG9tb3RoZXRpZQD#####AAAAAQAAAAMDAAAABT#wAAAAAAAAAAAABAAAAAv#####AAAAAQALQ1BvaW50SW1hZ2UA#####wEAAAAAEAACVyIBAAABAAAAAAMAAAAM#####wAAAAEACUNMb25ndWV1cgD#####AAAAAQAAAA0AAAABAP####8AAnAxAAQwLjAxAAAABT+EeuFHrhR7AAAAAQD#####AAJwMgAEMC44NQAAAAU#6zMzMzMzMwAAAAEA#####wACcDMABDAuMDcAAAAFP7HrhR64UewAAAABAP####8ABGFsZWEAB3JhbmQoMCkAAAAHEQAAAAUAAAAAAAAAAD#pgoz0Pw88AAAAAQD#####AANjYXMANHNpKGFsZWE8cDEsMSxzaShhbGVhPHAxK3AyLDIsc2koYWxlYTxwMStwMitwMywzLDQpKSkAAAACAAAAAAMEAAAABAAAABIAAAAEAAAADwAAAAU#8AAAAAAAAAAAAAIAAAAAAwQAAAAEAAAAEgAAAAMAAAAABAAAAA8AAAAEAAAAEAAAAAVAAAAAAAAAAAAAAAIAAAAAAwQAAAAEAAAAEgAAAAMAAAAAAwAAAAAEAAAADwAAAAQAAAAQAAAABAAAABEAAAAFQAgAAAAAAAAAAAAFQBAAAAAAAAD#####AAAAAQAIQ01hdHJpY2UA#####wACQTEAAAACAAAAAgAAAAUAAAAAAAAAAAAAAAUAAAAAAAAAAAAAAAUAAAAAAAAAAAAAAAU#xHrhR64UewAAABgA#####wACQTIAAAACAAAAAgAAAAU#6zMzMzMzMwAAAAU#pHrhR64Ue#####8AAAABAAxDTW9pbnNVbmFpcmUAAAAFP6R64UeuFHsAAAAFP+szMzMzMzMAAAAYAP####8AAkEzAAAAAgAAAAIAAAAFP8mZmZmZmZoAAAAZAAAABT#Qo9cKPXCkAAAABT#NcKPXCj1xAAAABT#MKPXCj1wpAAAAGAD#####AAJBNAAAAAIAAAACAAAAGQAAAAU#wzMzMzMzMwAAAAU#0euFHrhR7AAAAAU#0KPXCj1wpAAAAAU#zrhR64UeuAAAABgA#####wACQjEAAAACAAAAAQAAAAUAAAAAAAAAAAAAAAUAAAAAAAAAAAAAABgA#####wACQjIAAAACAAAAAQAAAAUAAAAAAAAAAAAAAAU#+ZmZmZmZmgAAABgA#####wACQjMAAAACAAAAAQAAAAUAAAAAAAAAAAAAAAU#+ZmZmZmZmgAAABgA#####wACQjQAAAACAAAAAQAAAAUAAAAAAAAAAAAAAAU#3Cj1wo9cKQAAAAYA#####wABQQApc2koY2FzPTEsQTEsc2koY2FzPTIsQTIsc2koY2FzPTMsQTMsQTQpKSkAAAACAAAAAAMIAAAABAAAABMAAAAFP#AAAAAAAAAAAAAEAAAAFAAAAAIAAAAAAwgAAAAEAAAAEwAAAAVAAAAAAAAAAAAAAAQAAAAVAAAAAgAAAAADCAAAAAQAAAATAAAABUAIAAAAAAAAAAAABAAAABYAAAAEAAAAFwAAAAYA#####wABQgApc2koY2FzPTEsQjEsc2koY2FzPTIsQjIsc2koY2FzPTMsQjMsQjQpKSkAAAACAAAAAAMIAAAABAAAABMAAAAFP#AAAAAAAAAAAAAEAAAAGAAAAAIAAAAAAwgAAAAEAAAAEwAAAAVAAAAAAAAAAAAAAAQAAAAZAAAAAgAAAAADCAAAAAQAAAATAAAABUAIAAAAAAAAAAAABAAAABoAAAAEAAAAGwAAABgA#####wABWAAAAAIAAAABAAAABQAAAAAAAAAAAAAABQAAAAAAAAAAAAAAAQD#####AAVhbGVhJwAOcmFuZCgwKSthbGVhKjAAAAADAAAAAAcRAAAABQAAAAAAAAAAP+rYUPYavTYAAAADAgAAAAQAAAASAAAABQAAAAAAAAAAAAAABgD#####AAFZAAVBKlgrQgAAAAMAAAAAAwIAAAAEAAAAHAAAAAQAAAAeAAAABAAAAB0AAAAIAP####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAHAAAAAAoAAAAJAAAAIAAAAAU#8AAAAAAAAAAAAAU#8AAAAAAAAAAAAAkAAAAgAAAABUAAAAAAAAAAAAAABT#wAAAAAAAA#####wAAAAEAG0NNYWNyb0NvbnN0cnVjdGlvbkl0ZXJhdGl2ZQD#####AAAA#wEAAP####8QQDGAAAAAAABAM4UeuFHrhgIB7+#7AAAAAAAAAAAAAAAFAAAAAAAAAAAACkNvbnN0cnVpcmUAAAAAAA4AAAAKAAAADwAAABAAAAARAAAAFAAAABUAAAAWAAAAFwAAABgAAAAZAAAAGgAAABsAAAASAAAAHgAAAAAAABOIAAAADAEAAP8AAAAAAAAADv##########Aquí está la figura obtenida :