Toutes les versions de cet article : [English] [Español] [français]
A continuación se muestra la figura que queremos realizar.
Capture los puntos A y B (que son puntos libres con coordenadas enteras en el referencial).
Encontrará que :
Si la recta es vertical, la ecuación se escribe en la forma x = constante.
Si los puntos se confunden, la ecuación de la recta desaparece.
Use el ícono  de la barra superior para crear una nueva figura, solicite una figura con un referencial (opción predeterminada) y un referencial ortonormal.
de la barra superior para crear una nueva figura, solicite una figura con un referencial (opción predeterminada) y un referencial ortonormal.
Desarrolle la barra de herramientas de puntos y haga clic sobre el ícono  para crear dos puntos de coordenadas enteras que nominará A y B (cliquear simplemente en un lugar a su elección).
para crear dos puntos de coordenadas enteras que nominará A y B (cliquear simplemente en un lugar a su elección).
Expanda la barra de herramientas de medición y use el icono (medición de abscisas en un referencial). Haga clic en el punto A e ingrese como nombre xA en el cuadro de diálogo.
(medición de abscisas en un referencial). Haga clic en el punto A e ingrese como nombre xA en el cuadro de diálogo.
Haga lo mismo para medir la abscisa del punto B y nombre esta medida xB.
Ahora usa el ícono  para medir las ordenadas de los puntos A y B y nombre estas medidas respectivamente como yA y yB.
para medir las ordenadas de los puntos A y B y nombre estas medidas respectivamente como yA y yB.
Ahora un comentario que será importante para lo que sigue. Al igual que con cualquier software que utiliza cálculos informáticos, los valores devueltos por los cálculos o funciones son los resultados de los cálculos realizados en valores que suelen ser aproximados y pueden verse afectados por pequeños errores de aproximación.
Veremos esto en un ejemplo.
Expanda la barra de visualizaciones y haga clic en el icono  de visualización de valores, haga clic en un lugar de la figura de su elección y solicite una visualización del valor de xA con 16 decimales como a continuación :
de visualización de valores, haga clic en un lugar de la figura de su elección y solicite una visualización del valor de xA con 16 decimales como a continuación :
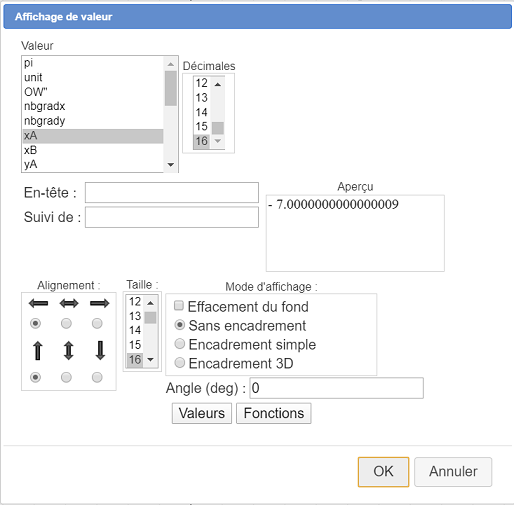
Aquí ve que el valor de xA no es exactamente un número entero. Este puede ser su caso, pero si cierra el cuadro de diálogo y captura el origen O del sistema de coordenadas, verá que, de vez en cuando, el decimal 16-ésimo no es cero.
En la continuación de esta figura, debemos tener cuidado de no usar más que números enteros en nuestros cálculos del MCD.
Use el ícono  para destruir la visualización del valor de xA y continuar con nuestra figura.
para destruir la visualización del valor de xA y continuar con nuestra figura.
Cuando nuestra recta no es vertical, su ecuación reducida es de la forma $y=ax+b$ avec $a=\displaystyle\frac{y_B-y_A}{x_B-x_A}$.
Expanda la barra de herramientas de cálculos y use el ícono  para crear un cálculo real llamado dx con la fórmula :
para crear un cálculo real llamado dx con la fórmula : int(xB-xA+0.5) como se muestra a continuación y valide :
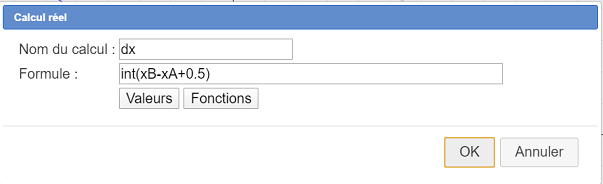
¿Por qué no usar simplemente xB-xA como fórmula ?
Luego usaremos dx en un cálculo de MCD y con la fórmula int(xB-xA+0.5) redondeamos la diferencia al entero más cercano para evitar errores de redondeo como se explicó anteriormente.
De la misma manera, cree los siguientes cálculos (herramienta  ) :
) :
| Nombre del cálculo | Fórmula | Comentario |
| dy | yB-yA | |
| g | MCD(abs(dx),abs(dy)) | Se necesitan valores absolutos porque la función MCD no acepta argumentos negativos |
| n | dy/g | Numerador de la fracción irreducible |
| d | dx/g | Denominador de la fracción irreducible |
La ordenada en el origen de nuestra recta (cuando no es vertical) viene dada por la fórmula $\displaystyle b=y_A-a x_A=yA-\frac{n}{d}xA=\frac{d y_A- n x_A}{d}$
Use el ícono nuevamente (herramienta  ) para crear los siguientes cálculos :
) para crear los siguientes cálculos :
| Nombre del cálculo | Fórmula | Comentario |
| nb | int(yA*d-n*xA+0.5) | |
| gb | MCD(abs(nb),abs(d)) | |
| n’ | nb/gb | Numerador de la fracción irreducible que representa b |
| d’ | d/gb | Denominador de la fracción irreducible que representa b |
| exist | dy<>0|dx<>0 |
exist será 1 si la recta existe y 0 en caso contrario. El operador <> devuelve 1 si los operandos izquierdo y derecho son diferentes y 0 en caso contrario. | es el operador booleano o |
| vert | dx=0 | Este cálculo contiene un test que devolverá 1 solo si los dos puntos tienen la misma abscisa |
Ahora vamos a crear una función de dos variables que se usará para mostrar la ecuación reducida de la recta en la forma y=ax+b cuando la recta no es vertical.
Expanda la barra de herramientas de cálculos y, a su derecha, haga clic en el icono  que muestra herramientas adicionales.
que muestra herramientas adicionales.

Elija el ítem Función real de dos variables y complete el cuadro de diálogo como se muestra a continuación.
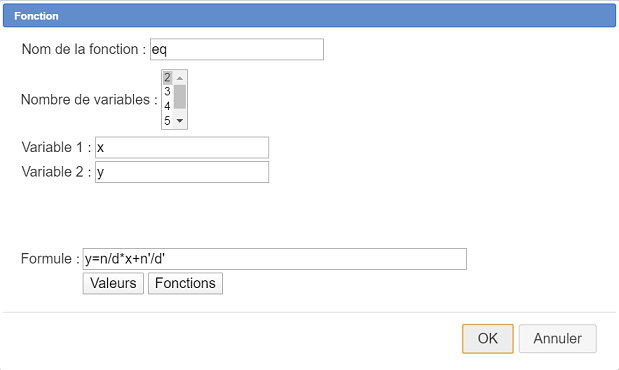
La fórmula para ingresar es : y=n/d*x+n’/d’
Ahora vamos a crear una función que se usará para mostrar la ecuación de la recta en la forma x=constante cuando la recta es vertical.
Expanda la barra de herramientas de cálculo y haga clic en el icono  .
.
Rellene el cuadro de diálogo como se muestra a continuación (no olvide desmarcar la casilla Trazar curva).
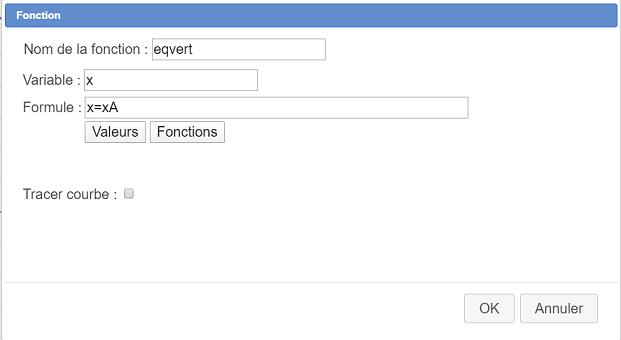
Ahora vamos a crear una visualización LaTeX que mostrará la ecuación reducida de la recta.
Esta pantalla LaTeX utilizará dos códigos LaTeX específicos de MathGraph32 :
Expanda la barra de visualizaciones y use el icono  .
.
Rellene el cuadro de diálogo de la siguiente manera :
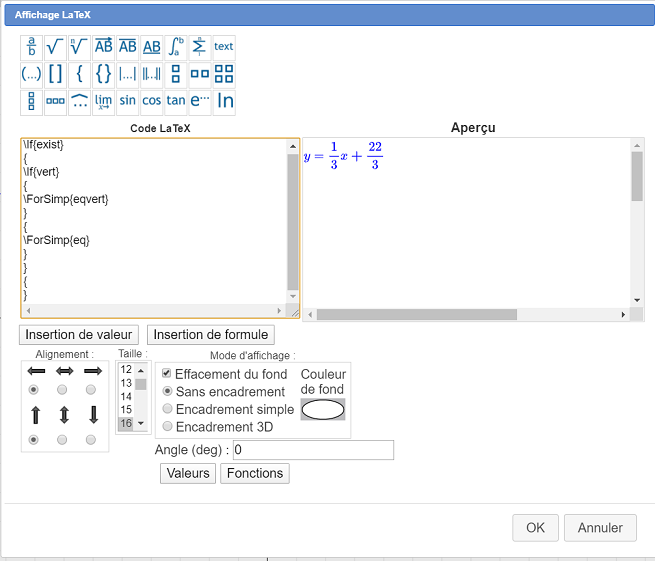
Aquí está el código LaTeX para usar :
Para resumir lo que hace este código LaTeX :
Si se confunden los dos puntos, no se hace nada (último par de llaves).
De lo contrario :
Ahora capture los puntos A y B para ver los diferentes casos en la figura.
Observaciones :
 de la barra de herramientas superior) y elija el ítem visualización de código LaTeX como se muestra a continuación.
de la barra de herramientas superior) y elija el ítem visualización de código LaTeX como se muestra a continuación.