Le but de cet article est de faire comprendre le lien entre calculs réels et complexes dans MathGraph32.
Il est réservé aux lecteurs ayant au moins un bagage mathématique de niveau Terminale S expert.
On peut définir dans MathGraph32 :
La règle de base est la suivante : La formule d’un calcul ou une fonction complexe peut utiliser n’importe quel calcul réel ou fonction réelle précédemment défini.
Démarrez MathGraph32 et vérifiez avec l’outil  que le mode de fonctionnement est bien Niveau avancé avec Nombres complexes.
que le mode de fonctionnement est bien Niveau avancé avec Nombres complexes.
Déroulez la barre des calculs et utilisez l’icône  pour créer la fonction réelle nommée f avec comme variable formelle x et comme formule
pour créer la fonction réelle nommée f avec comme variable formelle x et comme formule x².
Utilisez l’icône  pour créer un calcul nommé a avec comme formule
pour créer un calcul nommé a avec comme formule f(-1).
Utilisez l’icône 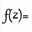 pour créer une fonction complexe g de la variable complexe z avec comme formule
pour créer une fonction complexe g de la variable complexe z avec comme formule f(z) comme ci-dessous :
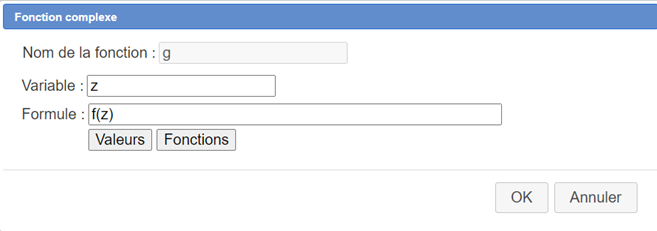
Utilisez maintenant l’icône 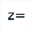 pour créer un calcul complexe nommé b avec comme formule
pour créer un calcul complexe nommé b avec comme formule g(1+i).
Pour voir les valeurs de a et de b, utilisez l’icône  de la barre supérieure.
de la barre supérieure.
Vous voyez que a a pour valeur $f(-1)=(-1)^2=1$ et que b a pour valeur $g(1+i)=f(1+i)=(1+i)^2=2i$
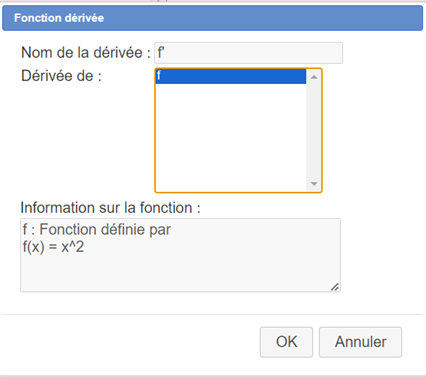
Maintenant utilisez l’icône 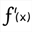 pour créer la fonction dérivée nommé f’ de la fonction f comme ci-dessous :
pour créer la fonction dérivée nommé f’ de la fonction f comme ci-dessous :
Utilisez l’icône  pour créer une fonction complexe g’ de la variable complexe z avec comme formule
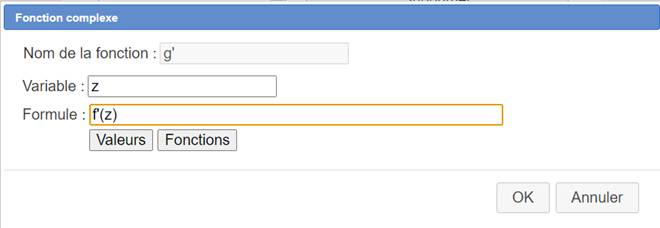
pour créer une fonction complexe g’ de la variable complexe z avec comme formule f'(z) comme ci-dessous :
Utilisez maintenant l’icône  pour créer un calcul complexe nommé c avec comme formule
pour créer un calcul complexe nommé c avec comme formule g(1+i) et utilisez l’outil  pour voir sa valeur.
pour voir sa valeur.
Comme la fonction réelle f est définie par $f(x)=x^2$ sa dérivée formelle f’ a pour formule $f’(x)=2x$ donc c a pour valeur $g’(1+i) = f’(1+i) = 2(1+i) = 2+2i$.
Nous allons maintenant créer une fonction réelle de deux variables z et I nommée h. Pour cela déroulez la barre des calculs et, à sa droite, cliquez sur l’icone  qui propose des outils supplémentaires. Cliquez sur l’item Fonction réelle de deux variables et remplissez la boîte de dialogue comme ci-dessous :
qui propose des outils supplémentaires. Cliquez sur l’item Fonction réelle de deux variables et remplissez la boîte de dialogue comme ci-dessous :
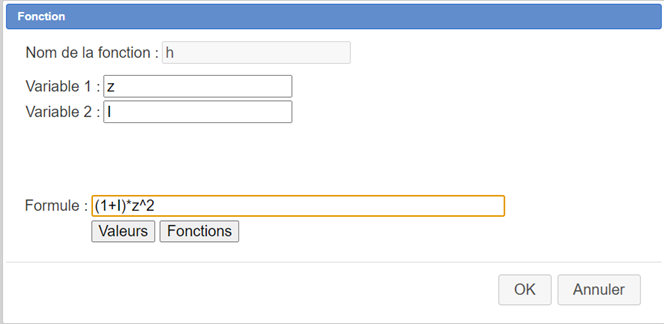
La formule utilisée pour h(z,I) est (1+I)*z^2.
A nouveau déroulez la barre des calculs et, à sa droite, cliquez sur l’icone  . Cliquez sur l’item Dérivée partielle.
. Cliquez sur l’item Dérivée partielle.
Remplissez la boîte de dialogue comme ci-dessous :
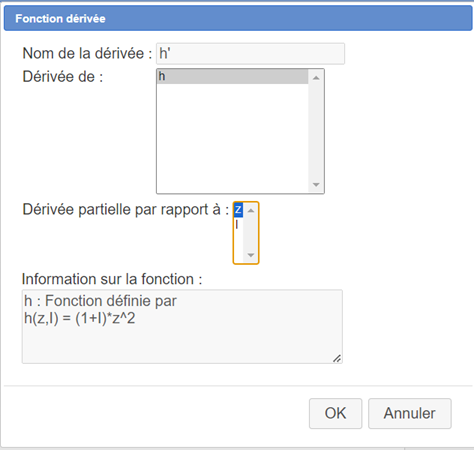
La formule (interne) utilisée par MathGraph32 pour cette dérivée partielle est donc $2(1+I)z$ (rappelons que MathGraph32 n’est pas un outil de calcul formel bien qu’il puisse utiliser des calculs de dérivées qui sont bien formels dans le logiciel).
Maintenant créons une fonction complexe d’une variable complexe nommée k’ comme ci-dessous :
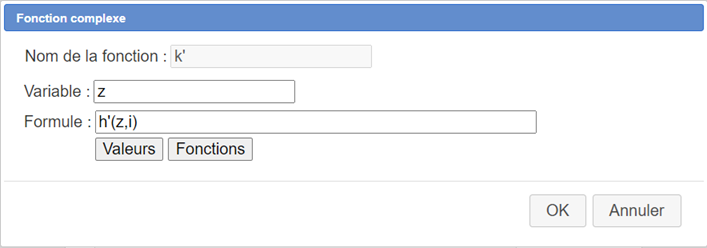
La formule définissant k’ est donc $h’(z,i)$. La formule utilisée de façon interne pour k’ est donc $k’(z)=2(1+i)z$
Utilisez maintenant l’icône  pour créer un calcul complexe nommé d avec comme formule $k’(1-i)$.
pour créer un calcul complexe nommé d avec comme formule $k’(1-i)$.
La valeur de d sera donc 2(1+i)(1-i)=4.
Utilisez maintenant l’icône  pour créer une fonction réelle de la variable réelle nommée p comme ci-dessous :
pour créer une fonction réelle de la variable réelle nommée p comme ci-dessous :
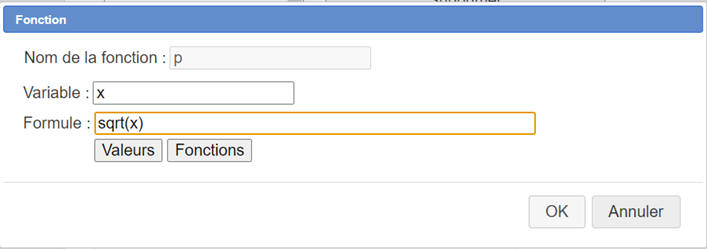
Utilisez maintenant l’icône  pour créer un calcul complexe nommé q avec comme formule p(4). La valeur de ce calcul complexe est $p(4)$. L’argument étant un réel strictement positif, il a bien une racine carrée unique et la valeur de de q est donc le complexe 2.
pour créer un calcul complexe nommé q avec comme formule p(4). La valeur de ce calcul complexe est $p(4)$. L’argument étant un réel strictement positif, il a bien une racine carrée unique et la valeur de de q est donc le complexe 2.
Utilisez de nouveau l’icône  pour créer un calcul complexe nommé r avec comme formule p(2*i). Un message vous avertit que ce calcul n’existe pas. En effet, dans C, le nombre complexe $2i$ n’a pas une racine carrée unique, mais il en a deux (qui sont $1+i$
pour créer un calcul complexe nommé r avec comme formule p(2*i). Un message vous avertit que ce calcul n’existe pas. En effet, dans C, le nombre complexe $2i$ n’a pas une racine carrée unique, mais il en a deux (qui sont $1+i$
Ci-dessous vous pouvez modifier les formules des objets créés :