Cet article a été adopté à la version JavaScript de MathGraph32.
Dans cet article, nous allons utiliser une fonction complexe d’une variable réelle, des lieux de points et d’objets et un éditeur de formule.
Voici ci-dessous la figure à réaliser. Dans le champ d’édition, vous pouvez une nouvelle formule pour f(z).
Vérifiez à l’aide de l’icône  (barre d’outils supérieure), que le niveau utilisé est le niveau Niveau avancé avec nombres complexes et que l’unité d’angle de la figure est le radian.
(barre d’outils supérieure), que le niveau utilisé est le niveau Niveau avancé avec nombres complexes et que l’unité d’angle de la figure est le radian.
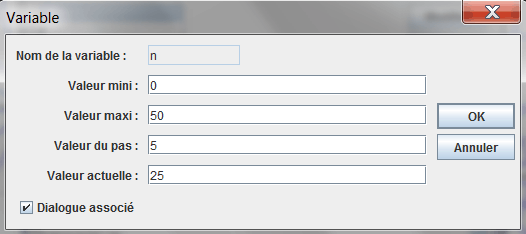
Utilisez l’icône  pour créer une nouvelle figure avec un repère. Remplissez la boîte de dialogue comme ci-dessous.
pour créer une nouvelle figure avec un repère. Remplissez la boîte de dialogue comme ci-dessous.
Utilisez l’outil  pour éloigner le point I du point O.
pour éloigner le point I du point O.
Utilisez l’icône  pour créer une variable comme ci-dessous :
pour créer une variable comme ci-dessous :
Utilisez l’icône  pour masquer les noms des points I et J.
pour masquer les noms des points I et J.
Nous allons maintenant définir une fonction complexe d’une variable complexe à l’aide de l’icône  .
.
Remplissez la boîte de dialogue comme ci-dessous :
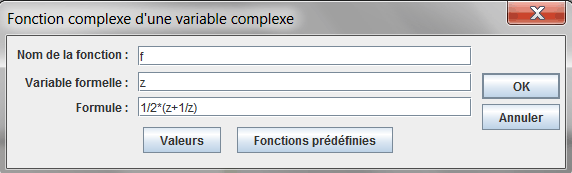
La formule utilisée est 1/2*(z+1/z)
Utilisez l’icône  pour créer un point libre et nommez-le A.
pour créer un point libre et nommez-le A.
Utilisez l’icône  pour créer une droite horizontale passant par A.
pour créer une droite horizontale passant par A.
Utilisez l’icône  pour créer un point lié à cette droite horizontale et nommez-le B.
pour créer un point lié à cette droite horizontale et nommez-le B.
Masquez la droite horizontale (icône  ).
).
Utilisez l’icône  de création d’un carré direct.
de création d’un carré direct.
Nommez C et D les deux points obtenus comme ci-dessus.
Utilisez l’icône  pour créer l’image du point B par la rotation de centre A et d’angle pi/2. Nommez ce point C. Créez ensuite le segment [AC].
pour créer l’image du point B par la rotation de centre A et d’angle pi/2. Nommez ce point C. Créez ensuite le segment [AC].
Créez un point lié au segment [AC] (icône  ).
).
Cliquez sur l’icône  de création d’image par une translation. Cliquez sur A puis sur B puis sur le point lié au segment [AC] pour créer son image par la translation. Joignez ensuite le point lié au segment [AC] et son image par la translation par un segment. Créez ensuite un point lié à ce segment et nommez-le M1.
de création d’image par une translation. Cliquez sur A puis sur B puis sur le point lié au segment [AC] pour créer son image par la translation. Joignez ensuite le point lié au segment [AC] et son image par la translation par un segment. Créez ensuite un point lié à ce segment et nommez-le M1.
Cliquez ensuite sur l’icône  pour mesurer l’affixe du point M1 et nommez cette mesure z1.
pour mesurer l’affixe du point M1 et nommez cette mesure z1.
Utilisez l’outil  pour créer le point d’affixe
pour créer le point d’affixe f(z1). Nommez ce point M’1.
Utilisez l’icône  pour créer le lieu du point M’1 généré par les déplacements du point M1 sur le segment auquel il est lié. Pour cela cliquez d’abord sur M’1, puis sur M1. Demandez un lieu de 200 points.
pour créer le lieu du point M’1 généré par les déplacements du point M1 sur le segment auquel il est lié. Pour cela cliquez d’abord sur M’1, puis sur M1. Demandez un lieu de 200 points.
Nous allons maintenant créer deux lieux d’objets.
Dans la palette de couleurs, activez la couleur grise.
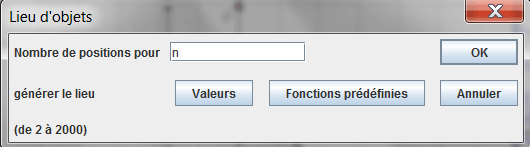
Utilisez l’icône  ) (lieu d’objet généré par point li. Cliquez sur le segment horizontal passant par M1, puis le point lié au segment [AC]. Demandez un lieu de n objets comme ci-dessous. Vous obtenez un quadrillage horizontal du carré.
) (lieu d’objet généré par point li. Cliquez sur le segment horizontal passant par M1, puis le point lié au segment [AC]. Demandez un lieu de n objets comme ci-dessous. Vous obtenez un quadrillage horizontal du carré.
Dans la palette de couleurs, activez la couleur bleue.
Utilisez à nouveau l’icône  .
.
Cliquez sur le lieu de points créé auparavant puis sur le point lié au segment [AC]. Comme précédemment, demandez un lieu formé de n objets.
Voici la figure obtenue :
Maintenant utilisez l’outil  pour masquer le segment [AC], le point M1, le segment horizontal passant par M1 et ses extrémités, le point M’1 ainsi que le lieu de points qui avait généré le lieu d’objets.
pour masquer le segment [AC], le point M1, le segment horizontal passant par M1 et ses extrémités, le point M’1 ainsi que le lieu de points qui avait généré le lieu d’objets.
Nous allons maintenant compléter le maillage dans le sens horizontal.
Activez la couleur noire dans la palette de couleurs.
Créez un point lié au segment [AB] (icône  ) puis créez l’image de ce point par la translation de vecteur AC (icône
) puis créez l’image de ce point par la translation de vecteur AC (icône  ). Joignez ces deux points par un segment.
). Joignez ces deux points par un segment.
Créez un point lié à ce dernier segment et nommez-le M2.
Mesurez l’affixe de ce point (icône  ). Nommez cette mesure z2.
). Nommez cette mesure z2.
Utilisez l’outil  pour créer le point d’affixe
pour créer le point d’affixe f(z2). Nommez ce point M’2.
Utilisez l’icône  pour créer le lieu du point M’2 généré par les déplacements du point M2 sur le segment auquel il est lié. Pour cela cliquez d’abord sur M’2, puis sur M2. Demandez un lieu de 200 points.
pour créer le lieu du point M’2 généré par les déplacements du point M2 sur le segment auquel il est lié. Pour cela cliquez d’abord sur M’2, puis sur M2. Demandez un lieu de 200 points.
Nous allons maintenant à nouveau créer deux lieux d’objets.
Dans la palette de couleurs, activez la couleur grise.
Utilisez l’icône  . Cliquez sur le segment vertical passant par M2, puis le point lié au segment [AB]. Demandez un lieu de n objets. Vous obtenez un quadrillage vertical du carré.
. Cliquez sur le segment vertical passant par M2, puis le point lié au segment [AB]. Demandez un lieu de n objets. Vous obtenez un quadrillage vertical du carré.
Dans la palette de couleurs, activez la couleur bleue.
Utilisez à nouveau l’icône  .
.
Cliquez sur le lieu de points créé auparavant puis sur le point lié au segment [AB]. Comme précédemment, demandez un lieu formé de n objets.
Maintenant masquez le point M2, le segment vertical passant par M2, ses extrémités, le point M’2 et le lieu de points ayant généré le lieu d’objets.
Nous allons maintenant créer un point intérieur au carré ABCD et son image par la transformation complexe.
Pour cela il faut d’abord créer un polygone avec l’outil  . Cliquez successivement sur A, B, D et C.
. Cliquez successivement sur A, B, D et C.
Activez ensuite l’icône  . Cliquez sur le polygone, puis à l’intérieur de celui-ci. Nommez M le nouveau point créé.
. Cliquez sur le polygone, puis à l’intérieur de celui-ci. Nommez M le nouveau point créé.
Utilisez l’icône  pour mesurer l’affixe de M et nommez cette affixe z.
pour mesurer l’affixe de M et nommez cette affixe z.
Dans la palette de couleurs, activez la couleur rouge.
Utilisez l’outil  pour créer le point d’affixe
pour créer le point d’affixe f(z). Nommez ce point M’.
Pour finir nous allons donner à l’utilisateur de modifier la formule de f(z) directement sur la figure à l’aide d’un éditeur de formule.
Dans la palette de couleurs, activez la couleur bleue.
Cliquez sur l’icône  (création d’un éditeur de formule) puis cliquez en haut et à gauche de la figure. Remplissez la boîte de dialogue comme ci-dessous.
(création d’un éditeur de formule) puis cliquez en haut et à gauche de la figure. Remplissez la boîte de dialogue comme ci-dessous.
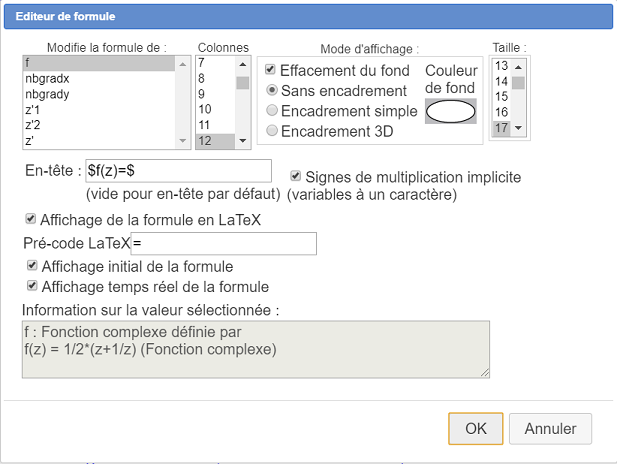
Vous pouvez ensuite déplacer cet éditeur avec l’outil  et en déplaçant son titre.
et en déplaçant son titre.
Vous pouvez maintenant modifier la formule de la fonction f directement dans cet éditeur. Essayez par exemple la formule z^2/(z+2/z).
Vous pouvez aussi capturer le point A pour déplacer le carré du maillage, déplacer B pour agrandir ou rétrécir le maillage et en bas et à droite utiliser les boutons + ou - pour augmenter ou diminuer le pas de maillage.