Toutes les versions de cet article : [English] [Español] [français]
This article has been adapted to the last JavaScript version of MathGraph32.
We will illustrate here a new theorem I discovered and demonstrated about 15 years ago.
If you are interested in the demonstration, please visit this page.
We want to illustrate a few properties of the transformation that, given three points A, B and C, associates to a point M the barycenter of (A ; MA), (B ; MB) et (C ; MC).
First we will create a macro construction that will create the image of a point M through this transformation.
Use icon  of the upper toolbar (new figure) and choose a figure without frame and with an unity length. Create four free points (icon
of the upper toolbar (new figure) and choose a figure without frame and with an unity length. Create four free points (icon  ) and name them A, B, C and M (icon
) and name them A, B, C and M (icon  ).
).
Expanding the measures toolbar, use tool  to create the measures of length MA, MB et MC (you can verify their existence by clicking on icon
to create the measures of length MA, MB et MC (you can verify their existence by clicking on icon  of the upper toolbar).
of the upper toolbar).
Now let us create the barycentre with tool  (expanding the points toolbar).
(expanding the points toolbar).
For this click first on A. A dialog box pops up to specify the coefficient. Use button Values to choose MA as coefficient then validate (the chosen coefficient blinks under point A). Proceed in the same way to affect coefficients MB et MC respectively to B and C then click on the red button  to create the barycenter.
to create the barycenter.
We are now ready to create our macro construction.
To manage the constructions , click in the upper toolbar on icon  to get more icons available.
to get more icons available.
Click on icon  (construction creation) and choose item Graphical sources objects choice.
(construction creation) and choose item Graphical sources objects choice.
Click on A, B, C et M (they start bliking) then click on icon  to indicate that the graphics sources objects are all there.
to indicate that the graphics sources objects are all there.
Again click on icon  and choose item Graphical final objects choice.
and choose item Graphical final objects choice.
Click on the barycenter created before then click on button  (this is the only final object).
(this is the only final object).
Now we have got to finalize our construction.
Click again on icon  , choose item Finish current construction and fill in the dialog box as shown here :
, choose item Finish current construction and fill in the dialog box as shown here :
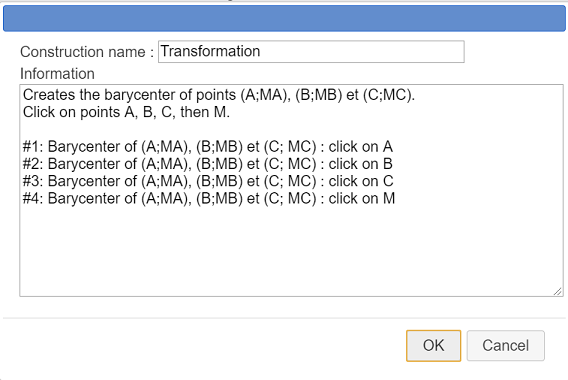
Here is the content of the Information editor (the four last lines are used to give information for each of the four sources objects when an user implements the construction ).
Creates the barycenter of points (A;MA), (B;MB) et (C;MC).
Click on points A, B, C, then M.
#1: Barycenter of (A;MA), (B;MB) et (C; MC) : click on A
#2: Barycenter of (A;MA), (B;MB) et (C; MC) : click on B
#3: Barycenter of (A;MA), (B;MB) et (C; MC) : click on C
#4: Barycenter of (A;MA), (B;MB) et (C; MC) : click on MOur construction is part of our figure abd will be saved along whith the figure itself. But we are going to save it in a separate file.
Use icon  (constructions management) eand choose item Save a construction of the figure. A dialog box pops up displaying a list of the constructions of the figure. Our construction Transformation is already selected.
(constructions management) eand choose item Save a construction of the figure. A dialog box pops up displaying a list of the constructions of the figure. Our construction Transformation is already selected.
Click on button Save file to save your construction in the directory of your choice (it is better to choose the same name for the file and the construction). Therefore the construction file will be Transformation.mgc.
If necessary you can get this file in the zip file underneath :
Use tool  to hide the first barycenter created (the final object for our first construction).
to hide the first barycenter created (the final object for our first construction).
Now create two free points (icon  ) and a circle with center the first point and going through the second point (icon
) and a circle with center the first point and going through the second point (icon  ).
).
Create a point linked to this circle (icône  ) and name it N.
) and name it N.
Click again on icon  (constructions management) and choose item Implement a construction of the figure. A dialog box pops up. the only available construction Transformation is already selected.
(constructions management) and choose item Implement a construction of the figure. A dialog box pops up. the only available construction Transformation is already selected.
Validate by OK.
A transient message is diplayed on the top right corner of the figure : Barycenter of (A ;MA), (B ;MB) and (C ; MC) : click on A. So click on point A.
Then click on B, on C then on point N (which stands for the point M of our initial construction).
A new point appears, created by our macro construction. If you capture point N you will see this new point vary (it is the barycenter of (A ;NA), (B ;NB) and (C ; NC)).
In the color palette, activate the blue color (or the color of your choice).
Now we will create the locus of this new point generated by the positions of point N on the circle it is linked to.
For this use  (Point locus generated by linked point).
(Point locus generated by linked point).
First click on the point created by the construction (poit traces of which will generate the locus) then on point N (linked point positions of which will generate the point locus). A dialog box pops up. Ask for 400 points and check the checkbox Closed locus. Validate.
Here is a figure you can get :
Now we are going to create a new macro construction that, given points A, B and C and the circle will create an only final object : the point locus we just created.
Use  (construction creation) and choose item Graphical sources objects choice.
(construction creation) and choose item Graphical sources objects choice.
Click on points A, B and C the on teh circle. Then click on button  .
.
Again use icon  and choose item Graphical final objects choice.
and choose item Graphical final objects choice.
Click on the point locus you just created the click on button  (we have got only a final object).
(we have got only a final object).
Now we must finalize our construction. Click again on icon  and choose icon Finish current construction.
and choose icon Finish current construction.
Fill in the dialog box as shown underneath.
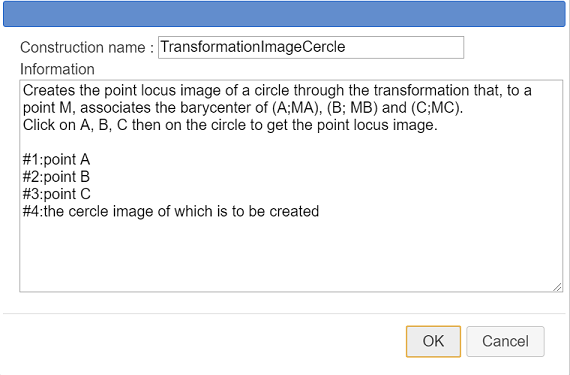
Here is the content of the Information editor :
Creates the point locus image of a circle through the transformation that, to a point M, associates the barycenter of (A;MA), (B; MB) and (C;MC).
Click on A, B, C then on the circle to get the point locus image.
#1:point A
#2:point B
#3:point C
#4:the cercle image of which is to be createdLet us save this construction in a separate file.
Use icon  (constructions management) and choose item Save a construction of the figure.
(constructions management) and choose item Save a construction of the figure.
Select the construction TransformationImageCercle and click on button Save file to save this construction in the same directory as the first one (the saved file will be TransformationImageCercle .mgc).
You can also download this construction from the zip file underneath.
Now we are going to use the last construction in another figure.
First save you figure in a file then choose icon  to create a new igure without frame and with an unity length.
to create a new igure without frame and with an unity length.
Create two free points (icon  ) and a circle with center the first point and going through the second one (icone
) and a circle with center the first point and going through the second one (icone ). Name the center O (icon
). Name the center O (icon ).
).
With tool  create three points linked to this circle and name them A, B and C. Joint these three points by three segments (tool
create three points linked to this circle and name them A, B and C. Joint these three points by three segments (tool  ).
).
Use icon  (constructions management) and choose item Incorporate a construction from file and browse to the construction TransformationImageCercle in the directory you saved it to before.
(constructions management) and choose item Incorporate a construction from file and browse to the construction TransformationImageCercle in the directory you saved it to before.
Use again icon  and choose item Implement a construction of the figure. Our only construction TransformationImageCercle is already selected. Click on button Implement.
and choose item Implement a construction of the figure. Our only construction TransformationImageCercle is already selected. Click on button Implement.
Fisrt click on points A, B and C then on the circle.
The image locus appears (finla object of the construction). You can see it seems to be in a shape of a real triangle with the summits on the sides of triangle ABC.
Use icon  to create a point linked to the circle. Name it M.
to create a point linked to the circle. Name it M.
We are also going to create the image of M through the transformation.
Use icon  (constructions management) and choose item Incorporate a construction form file and browse to the contruction file named Transformation in the directory you saved it to.
(constructions management) and choose item Incorporate a construction form file and browse to the contruction file named Transformation in the directory you saved it to.
Again use icon  and choose item Implement a construction of the figure.
and choose item Implement a construction of the figure.
In the list of constructions displayed, click on the construction named Transformation and click on the button Implement.
Click (in this order) on A, B, C then M.
The point image of M through our transformation appears. Of course it is on the point locus we created before. Name this point G.
Here is the figure you get :
Capture point M et and watch how point G moves on the image locus.
We want now to illustrate the image of the interior of the circle circumscribed of triangle ABC.
Create segment [OA] (icon  ) and a point liked to this segment we will name P (tool
) and a point liked to this segment we will name P (tool  ).
).
Now create the circle of center O and going through PP (icon ![]() ).
).
Again use icon  and choose item Implement a construction of the figure.
and choose item Implement a construction of the figure.
This time select the construction TransformationImagCercle and click on button Implement.
Click on points A, B and C the on the circle with center O and going through P. The point locus image of this circle appears like underneath :
Now we will create thee objet locus of this point locus generated by the positions of point P on segment [OA].
In the color palette, activate the red color.
Expand the locuses toolbar and click on icon  (object locus generated by linked point).
(object locus generated by linked point).
First you are asked to click on the object trace of which will generate the locus : click on the last point locus generated by the construction (it starts blinking).
The you are asked to click on the linked point positions of which will generate the object locus : click on point P.
On the dialog box popping up ask for 30 objects.
Underneath is the final figure.
To be noted : you can change the color of the object locus with tool  but not it’s line style that is the line style of the point locus that generated the object locus.
but not it’s line style that is the line style of the point locus that generated the object locus.
Capture point P. This figure seems to infer that the image of the interior of the circle circumscribed to trangle ABC is the interior of the triangle image of this circle.
Captur also points A, B et C.