Toutes les versions de cet article : [English] [Español] [français]
Cet article a été adapté à la version JavaScript de MathGraph32.
MathGraph32 permet de créer des suites du type $u_{n+1}=f(u_n)$ et de les représenter graphiquement.
Cet article étudie les suites récurrentes complexes de la forme $u_{n + 1} = f\left( {u_n } \right)$ avec $f(z) = \frac{1}{2}(z + \frac{a}{z})$.
On généralise ainsi l’algorithme de Babylone de calcul d’une racine carrée dans l’ensemble des nombres complexes.
L’article montre comment MathGraph32 permet de visualiser très simplement des résultats intéressants avec des figures animées en ligne par MathGraph32.
Cliquez ici pour consulter cet article.
Créez une nouvelle figure à l’aide de l’icône  et choisissez un repère orthonormal avec vecteurs.
et choisissez un repère orthonormal avec vecteurs.
A l’aide de l’icône  créez un point libre et nommez-le M.
créez un point libre et nommez-le M.
Déroulez la barre d’outil des mesures et utilisez l’icône  pour mesurer l’affixe du point M (il suffit de cliquer sur M). Une boîte de dialogue s’ouvre pour choisir le nom de cette mesure. Entrez par exemple zM.
pour mesurer l’affixe du point M (il suffit de cliquer sur M). Une boîte de dialogue s’ouvre pour choisir le nom de cette mesure. Entrez par exemple zM.
Déroulez la barre d’outil des calculs et utilisez l’icône 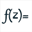 pour créer une fonction complexe de la variable complexe nommée f de variable nommée t et définie par la formule f(t)=t+1/t^2.
pour créer une fonction complexe de la variable complexe nommée f de variable nommée t et définie par la formule f(t)=t+1/t^2.
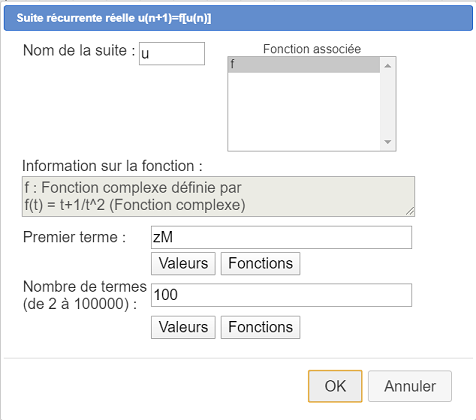
Créons maintenant une suite récurrente complexe nommée u du type u(n+1)=f[u(n)] dont le premier terme sera l’affixe que nous venons de mesurer.
Pour cela, dans la barre d’outil des calculs, utilisez l’icône 
Une boîte de dialogue s’ouvre.
Entrez u dans le champ Nom.
La fonction f est déjà sélectionnée.
Utilisez le bouton Valeurs pour choisir zM qui représente l’affixe de M dans le champ Premier terme.
Dans le champ Nombre de termes entrez 100.
Validez par OK.
Voici la boîte de dialogue avant validation :
Créons maintenant le graphe de cette suite.
Activez la couleur bleue et le style de trait pointillé.
Utilisez ensuite l’icône  (graphe d’une suite récurrente complexe).
(graphe d’une suite récurrente complexe).
Une boîte de dialogue s’ouvre comme celle-ci :
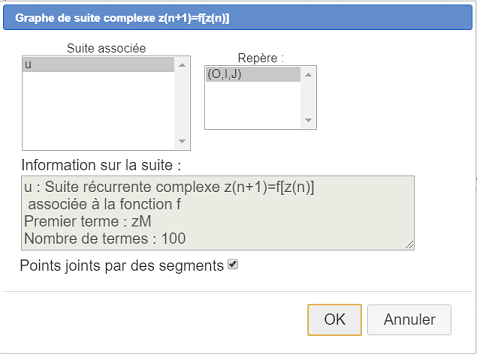
La suite u est déjà sélectionnée. Validez les choix par défaut.
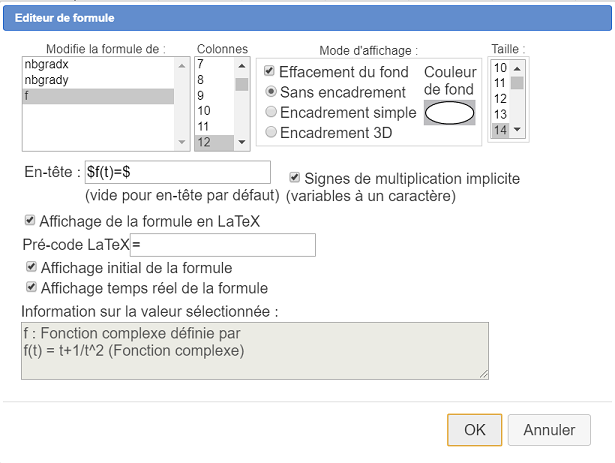
Maintenant créons un éditeur de formule qui nous permettra de modifier la formule de f(t) directement sur la figure.
En déroulant la barre d’outil des calculs, utilisez l’icône  et cliquez en haut et à gauche de la figure (pas trop à gauche).
et cliquez en haut et à gauche de la figure (pas trop à gauche).
Une boîte de dialogue s’ouvre. Remplissez-la comme ci-dessus (attention de bien affecter l’éditeur à la fonction complexe f)
Pour finir nous allons afficher les termes de cette suite sur la figure.
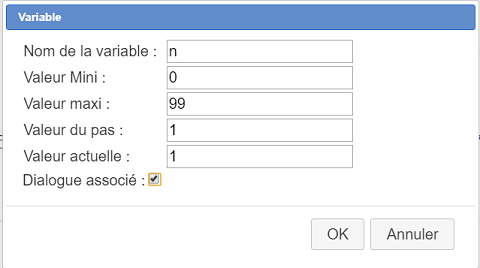
Nous allons pour cela utiliser une variable dont les valeurs entières iront de 0 à 99 (nous avons choisi 100 termes pour la suite et les indices commencent à 0).
Utilisez l’icône  et remplissez la boîte de dialogue comme ci-dessous (les variables sont toujours insérées en tête de la liste des objets créés). N’oubliez pas de cocher la case Dialogue associé.
et remplissez la boîte de dialogue comme ci-dessous (les variables sont toujours insérées en tête de la liste des objets créés). N’oubliez pas de cocher la case Dialogue associé.
.
Déroulez la barre d’ouil des calculs et utilisez l’icône  pour créer un calcul complexe nommé un avec comme formule f(n).
pour créer un calcul complexe nommé un avec comme formule f(n).
Maintenant utilisons un affichage LaTeX dynamique.
Déroulez la barre d’outil des affichages et utilisez l’icône  pour créer un affichage LaTeX libre et cliquez en haut et à gauche de la figure, sous l’éditeur de formule. Remplissez la boîte de dialogue comme ci-dessous. Vous pouvez utiliser le bouton Insertion de valeur pour insérer le code LaTeX spécial affichant les valeurs de n et de un (pour un il faut demander 12 décimales).
pour créer un affichage LaTeX libre et cliquez en haut et à gauche de la figure, sous l’éditeur de formule. Remplissez la boîte de dialogue comme ci-dessous. Vous pouvez utiliser le bouton Insertion de valeur pour insérer le code LaTeX spécial affichant les valeurs de n et de un (pour un il faut demander 12 décimales).
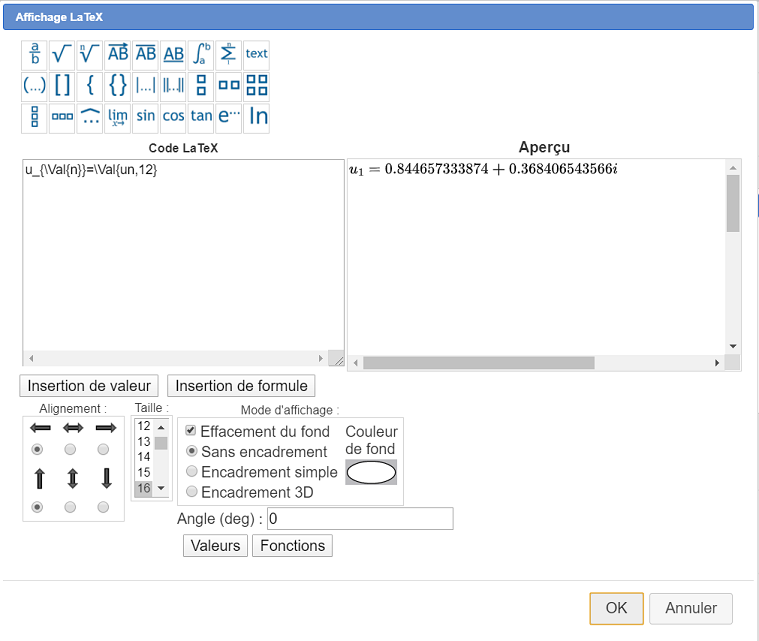
Voici le code LaTeX à utiliser :
La figure est prête.
Vous pouvez maintenant faire varier les valeurs de n en cliquant en bas et à droite de la figure sur les boutons + et -.
Vous pouvez la voir ci-dessous animée par le moteur JavaScript de MathGraph32.
Vous pouvez capturer le point M.
Changez par exemple la formule de f(t) par :
et capturez M : la suite converge soit vers 2i soit vers -2i (suite complexe de Babylone).