Calcul et représentation des nombres complexes

Cet article a été adapté à la version JavaScript de MathGraph32.

MathGraph32 permet le calcul et la représentation graphique des nombres complexes.

Il a été le premier logiciel de géométrie dynamique en langue française à le faire.

Il est possible d’utiliser les fonctions transcendantes usuelles sur les complexes, de créer un point défini par son affixe dans un repère, de mesurer l’affixe d’un point dans un repère, de créer des fonctions complexes d’une, deux ou trois variables complexes, des suites récurrentes complexes du type u(n+1) = f[u(n)] et de représenter graphiquement de telles suites.

Un calcul complexe peut utiliser tout calcul ou toute mesure réel ou complexes définis auparavant.

Un calcul réel ne peut utiliser que des calculs ou mesures réels précédemment définis.

Pour pouvoir utiliser dans un calcul réel la partie réelle, imaginaire, l’argument ou le module d’un complexe, il faut auparavant créer un calcul réel égal à la partie imaginaire, réelle, l’argument ou le module du complexe.

Vous pouvez voir un autre exemple d’utilisation des nombres complexes dans cet article.

Prenons un exemple : Nous désirons visualiser l’image du cercle de centre O et de rayon 1 par la transformation complexe associée à la fonction f définie par f(z) = z + 1/z^n où n est un entier naturel compris entre 1 et 10.

Pour créer une nouvelle figure, utilisez l’icône et demandez un repère orthonormal avec vecteurs. Vous pouvez appeler les vecteurs du repère u et v si vous le souhaitez en cliquant sur l’icône et en cliquant sur les affichages LaTeX des deux vecteurs.

A l’aide de l’icône pour créer le cercle de centre O et passant par I (I est le point d’abscisse 1 sur l’axe des abscisses. Son nom est caché).

Utilisez l’icône 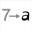pour créer une variable nommée n avec 1 comme valeur minimale, 10 comme valeur maximale, 1 comme pas et 2 comme valeur actuelle. Cochez la case Dialogue associé.

Utilisez l’icône 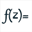pour créer une fonction complexe de la variable complexe nommée f avec comme variable formelle t et comme formule t+1/t^n.

Déroulez la barre d’outil des affichages et, à sa droite cliquez sur l’icône (création d’une nouvelle macro). Choisissez l’item Macro d’incrémentation de variable. Cliquez à un endroit libre en haut et à gauche de la figure.

Une boîte de dialogue apparaît. Comme intitulé de la macro entrez Augmenter n. La variable n est déjà sélectionnée. Validez.

Créez de la même façon une macro de décrémentation de la variable n ayant comme intitulé Diminuer n en cliquant sur l’icône et en choisissant l’item Macro de décrémentation de variable.

Utilisez l’icône pour créer en haut et à gauche un affichage de la valeur de la variable n (vous pouvez utiliser le bouton Liste des valeurs pour sélectionner n).

A l’aide de l’icône , créez un point lié au cercle de centre O déjà créé et nommez ce point M.

Dans la barre d’outil des mesures, utilisez l’icône pour mesurer l’affixe de M (il suffit de cliquer sur M) et nommez la z.

Utilisez l’icône 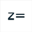pour créer un calcul complexe nommé z’ contenant comme formule f(z).

Utilisez l’icône pour créer le point d’affixe z’ et nommez ce point M’.

Il reste à créer le lieu du point M’ généré par les positions de M sur le cercle.

Dans la palette de couleurs, activez la couleur rouge.

Utilisez l’icône . Cliquez en premier sur M’ puis sur M. Dans la boîte de dialogue qui s’ouvre, cochez la case Lieu fermé et demandez 300 points. Validez.

La figure est prête.

Vous pouvez voir cette figure en action ci-dessous grâce à la librairie JavaScript de MathGraph32 :