Toutes les versions de cet article : [Español] [français]
Desde la versión 3.5, MathGraph32 posee funciones LaTeX especiales avanzadas que vamos a ilustrar en este ejemplo.
Deseamos trazar la curva representativa de una función polinómica de grado inferior o igual a 2 y una tangente a la curva.
Para eso, creamos una nueva figura con el menú Crear - Nueva figura con - Referencial sin vectores y elegimos un referencial ortonormal.
Creamos arriba y a la izquierda de la figura un primer cursor con valores enteros que hará variar los valores de a. Para eso, cliqueamos sobre el icono![]() luego cliqueamos arriba y a la izquierda de la figura.
luego cliqueamos arriba y a la izquierda de la figura.
Completamos la caja de diálogo como se ve abajo y luego validamos (no olvidar de marcar la casilla Cursor con valores enteros).
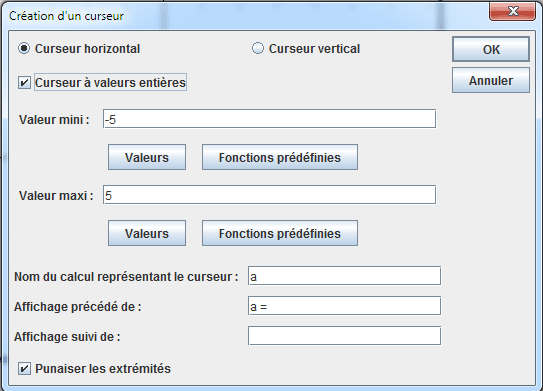
De manera análoga creamos debajo del cursor dos nuevos cursores con valores enteros que harán variar los valores de b y c.
A tener en cuenta : Los extremos izquierdo y derecho del cursor están fijados por defecto. Si deseamos desplazar el cursor, comenzamos por liberar el extremo izquierdo con la herramienta ![]() luego capturamos el extremo izquierdo con la herramienta de captura
luego capturamos el extremo izquierdo con la herramienta de captura ![]()
En la paleta de color, activamos el color azul.
Utilizamos ahora el icono ![]() para crear la función y obtener su curva.
para crear la función y obtener su curva.
Llenamos la caja de diálogo como se ve abajo y validamos. La curva de la función aparece en azul.
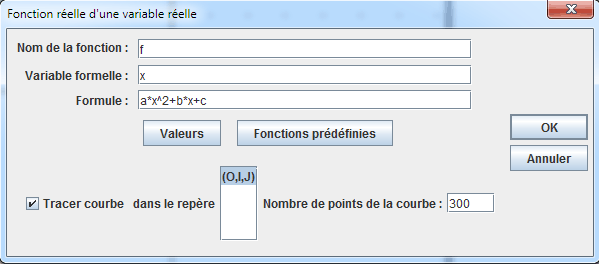
Para escribir sobre la figura la fórmula de f(x) bajo la forma más simple posible, vamos a utilizar una construcción proporcionada con MathGraph32 (esta construcción sólo está disponible si se utiliza la versión 3.5 o posterior).
Utilizamos el menú Construcciones - Implementar una construcción predefinida.
En la caja de diálogo que se abre, abrimos la carpeta Algebra, cliqueamos sobre la construcción llamada Polinomio Segundo Grado Simplificado y luego validamos.
Aparece la caja de diálogo de elección de los objetos fuentes.
En la lista de la izquierda, se selecciona el número 1. Le asociamos a como se ve abajo.
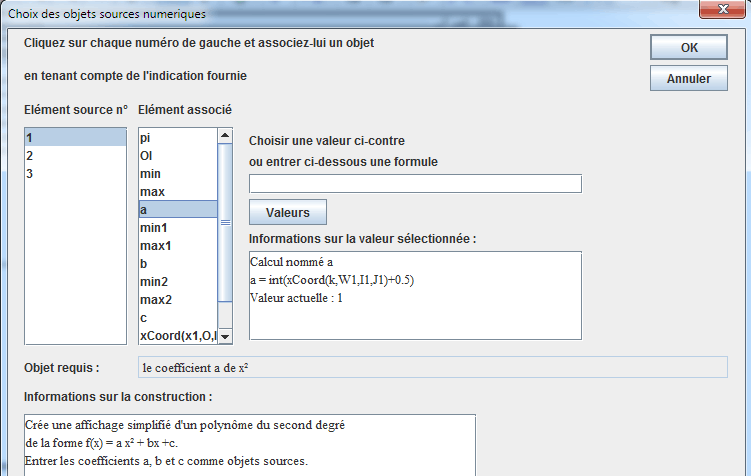
Del mismo modo, se selecciona el número 2 en la lista de la izquierda y se le asocia b luego se selecciona el número 3 y se le asocia c, luego validamos.
La visualización de la fórmula aparece arriba y a la izquierda de la figura, en negro. Utilizamos la herramienta ![]() para desplazarla arriba y a la derecha de la figura luego con la herramienta
para desplazarla arriba y a la derecha de la figura luego con la herramienta ![]() le damos el color azul.
le damos el color azul.
En la paleta de colores, activamos el color rojo y con la ayuda del icono ![]() creamos un punto ligado a la curva (la curva es en realidad un lugar de puntos). Utilizamos el icono
creamos un punto ligado a la curva (la curva es en realidad un lugar de puntos). Utilizamos el icono ![]() para nombrar este punto M.
para nombrar este punto M.
Medimos ahora la abscisa del punto M en el referencial con la herramienta ![]() .
.
Vamos ahora a pedir a MathGraph32 crear la tangente a la curva de la función f en el punto M. Para eso utilizamos la herramienta ![]() . Una caja de diálogo se abre. La completamos como se ve abajo.
. Una caja de diálogo se abre. La completamos como se ve abajo.
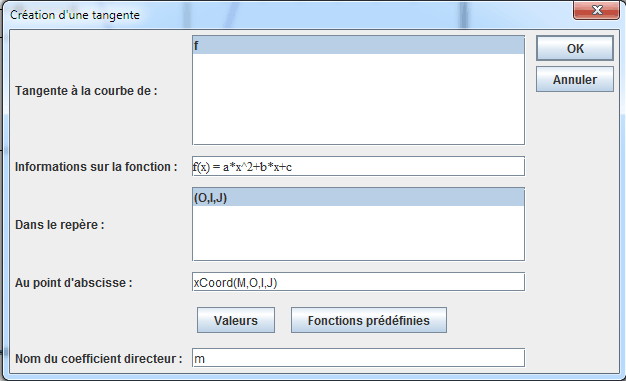
La tangente en M aparece. Es necesario observar que se trata de una verdadera tangente resultante de un cálculo interno de una derivada formal.
Pidamos ahora a MathGraph32 visualizar la ecuación reducida de esta tangente. Cliqueamos sobre el ícono ![]() . Se nos pide en la línea de indicación cliquear sobre lugar dónde se visualizará esta ecuación. Cliqueamos debajo del último cursor y luego completamos la caja de diálogo como se ve a continuación :
. Se nos pide en la línea de indicación cliquear sobre lugar dónde se visualizará esta ecuación. Cliqueamos debajo del último cursor y luego completamos la caja de diálogo como se ve a continuación :
Podemos ahora capturar el punto M y hacer variar los valores de a, b y c. Observamos que la fórmula de la función siempre se escribe bajo la forma más simple posible.
A continuación se tiene la figura obtenida :