Calcul matriciel : Système de 4 équations à 4 inconnues écrit de façon naturelle.

modification vendredi 27 août 2021.

Toutes les versions de cet article : [English] [Español] [français]

Dans ce tutoriel, nous allons écrire une figure où on peut écrire un système de 4 équations à 4 inconnues de façon naturelle et le résoudre.

Voici ci-dessous la figure en action :

Pour créer cette figure, vous devez utiliser la version 6.8.0 de MathGraph32 ou une version ultérieure.

Si vous ne souhaitez pas suivre toutes les étapes vous pouvez ouvrir cette figure à l’aide de son code Base 64 ci-dessous :

TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAAAAAAAAQAAAEv#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAJQ0ZvbmNOVmFyAP####8ABWVxdWExAAUzKng9Mf####8AAAABAApDT3BlcmF0aW9uCAAAAAMCAAAAAUAIAAAAAAAA#####wAAAAIAEUNWYXJpYWJsZUZvcm1lbGxlAAAAAAAAAAE#8AAAAAAAAAAAAAQAAXgAAXkAAXoAAXQAAAACAP####8ABWVxdWEyAAV4K3k9MgAAAAMIAAAAAwAAAAAEAAAAAAAAAAQAAAABAAAAAUAAAAAAAAAAAAAABAABeAABeQABegABdAAAAAIA#####wAFZXF1YTMAB3greSt6PTMAAAADCAAAAAMAAAAAAwAAAAAEAAAAAAAAAAQAAAABAAAABAAAAAIAAAABQAgAAAAAAAAAAAAEAAF4AAF5AAF6AAF0AAAAAgD#####AAVlcXVhNAAJeCt5K3o9NC10AAAAAwgAAAADAAAAAAMAAAAABAAAAAAAAAAEAAAAAQAAAAQAAAACAAAAAwEAAAABQBAAAAAAAAAAAAAEAAAAAwAAAAQAAXgAAXkAAXoAAXT#####AAAABAAPQ0VkaXRldXJGb3JtdWxlAP####8AAAAAAQAA#####xBAVaAAAAAAAEAxhR64UeuGAAH###8AAAACAAAAAAAAAAEAAAAAAAAAAAAAAAEADEVxdWF0aW9uIDEgOgAAABQBAQACXCwBAQAAAAUA#####wAAAAABAAD#####EEBVoAAAAAAAQE5Cj1wo9cMAAf###wAAAAIAAAAAAAAAAQAAAAAAAAAAAAAAAgAMRXF1YXRpb24gMiA6AAAAFAEBAAJcLAEBAAAABQD#####AAAAAAEAAP####8QQFUgAAAAAABAWWFHrhR64gAB####AAAAAgAAAAAAAAABAAAAAAAAAAAAAAADAAxFcXVhdGlvbiAzIDoAAAAUAQEAAlwsAQEAAAAFAP####8AAAAAAQAA#####xBAVOAAAAAAAEBicKPXCj1xAAH###8AAAACAAAAAAAAAAEAAAAAAAAAAAAAAAQADEVxdWF0aW9uIDQgOgAAABQBAQACXCwBAQAAAAIA#####wADZGYxACxnYXVjaGUoZXF1YTEoeCx5LHosdCkpLWRyb2l0KGVxdWExKHgseSx6LHQpKQAAAAMB#####wAAAAIACUNGb25jdGlvbhT#####AAAAAQASQ0FwcGVsRm9uY3Rpb25OVmFyAAAABAAAAAEAAAAEAAAAAAAAAAQAAAABAAAABAAAAAIAAAAEAAAAAwAAAAYVAAAABwAAAAQAAAABAAAABAAAAAAAAAAEAAAAAQAAAAQAAAACAAAABAAAAAMAAAAEAAF4AAF5AAF6AAF0AAAAAgD#####AANkZjIALGdhdWNoZShlcXVhMih4LHkseix0KSktZHJvaXQoZXF1YTIoeCx5LHosdCkpAAAAAwEAAAAGFAAAAAcAAAAEAAAAAgAAAAQAAAAAAAAABAAAAAEAAAAEAAAAAgAAAAQAAAADAAAABhUAAAAHAAAABAAAAAIAAAAEAAAAAAAAAAQAAAABAAAABAAAAAIAAAAEAAAAAwAAAAQAAXgAAXkAAXoAAXQAAAACAP####8AA2RmMwAsZ2F1Y2hlKGVxdWEzKHgseSx6LHQpKS1kcm9pdChlcXVhMyh4LHkseix0KSkAAAADAQAAAAYUAAAABwAAAAQAAAADAAAABAAAAAAAAAAEAAAAAQAAAAQAAAACAAAABAAAAAMAAAAGFQAAAAcAAAAEAAAAAwAAAAQAAAAAAAAABAAAAAEAAAAEAAAAAgAAAAQAAAADAAAABAABeAABeQABegABdAAAAAIA#####wADZGY0ACxnYXVjaGUoZXF1YTQoeCx5LHosdCkpLWRyb2l0KGVxdWE0KHgseSx6LHQpKQAAAAMBAAAABhQAAAAHAAAABAAAAAQAAAAEAAAAAAAAAAQAAAABAAAABAAAAAIAAAAEAAAAAwAAAAYVAAAABwAAAAQAAAAEAAAABAAAAAAAAAAEAAAAAQAAAAQAAAACAAAABAAAAAMAAAAEAAF4AAF5AAF6AAF0#####wAAAAEABUNGb25jAP####8ABHplcm8AEmFicyh4KTwwLjAwMDAwMDAwMQAAAAMEAAAABgAAAAAEAAAAAAAAAAE+ES4L6CbWlQABeP####8AAAABABFDRGVyaXZlZVBhcnRpZWxsZQD#####AAVkZXJ4MQAAAAkAAAAAAAAACQD#####AAVkZXJ5MQAAAAkAAAABAAAACQD#####AAVkZXJ6MQAAAAkAAAACAAAACQD#####AAVkZXJ0MQAAAAkAAAADAAAACQD#####AAVkZXJ4MgAAAAoAAAAAAAAACQD#####AAVkZXJ5MgAAAAoAAAABAAAACQD#####AAVkZXJ6MgAAAAoAAAACAAAACQD#####AAVkZXJ0MgAAAAoAAAADAAAACQD#####AAVkZXJ4MwAAAAsAAAAAAAAACQD#####AAVkZXJ5MwAAAAsAAAABAAAACQD#####AAVkZXJ6MwAAAAsAAAACAAAACQD#####AAVkZXJ0MwAAAAsAAAADAAAACQD#####AAVkZXJ4NAAAAAwAAAAAAAAACQD#####AAVkZXJ5NAAAAAwAAAABAAAACQD#####AAVkZXJ6NAAAAAwAAAACAAAACQD#####AAVkZXJ0NAAAAAwAAAAD#####wAAAAEACENNYXRyaWNlAP####8AAUEAAAAEAAAABAAAAAcAAAAEAAAADgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAADwAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAEAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAEQAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAEgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAEwAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAFAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAFQAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAFgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAFwAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAGAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAGQAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAGgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAGwAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAHAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAHQAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAP####8AAAABABRDSW1wbGVtZW50YXRpb25Qcm90bwD#####AAxEw6l0ZXJtaW5hbnQAAAABAAAAAQAAAAEAAAAe#####wAAAAEACENDYWxjTWF0AAAAAB8ABmRldE1hdAAIZGV0ZXIoQSkAAAAGF#####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAAe#####wAAAAEAB0NDYWxjdWwBAAAAHwAEZGV0QQALZGV0TWF0KDEsMSn#####AAAAAQAIQ1Rlcm1NYXQAAAAgAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAAAAAACgD#####AAFCAAAABAAAAAH#####AAAAAQAMQ01vaW5zVW5haXJlAAAABwAAAAQAAAAJAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAEAAAAAcAAAAEAAAACgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAABAAAAAHAAAABAAAAAsAAAABAAAAAAAAAAAAAAABAAAAAAAAAAAAAAABAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAQAAAABwAAAAQAAAAMAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAADAD#####AAFYAAhBXigtMSkqQgAAAAMC#####wAAAAEACkNQdWlzc2FuY2UAAAANAAAAHgAAABAAAAABP#AAAAAAAAAAAAANAAAAIgAAAA4A#####wACeDAABlgoMSwxKQAAAA8AAAAjAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAAAAAADgD#####AAJ5MAAGWCgyLDEpAAAADwAAACMAAAABQAAAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AAnowAAZYKDMsMSkAAAAPAAAAIwAAAAFACAAAAAAAAAAAAAE#8AAAAAAAAAAAAA4A#####wACdDAABlgoNCwxKQAAAA8AAAAjAAAAAUAQAAAAAAAAAAAAAT#wAAAAAAAAAAAADgD#####AAJ4MQAJMStyYW5kKDApAAAAAwAAAAABP#AAAAAAAAAAAAAGEQAAAAEAAAAAAAAAAD#JDHdg9gPoAAAADgD#####AAJ4MgAJMStyYW5kKDApAAAAAwAAAAABP#AAAAAAAAAAAAAGEQAAAAEAAAAAAAAAAD#HAt+KIoUAAAAADgD#####AAJ4MwAJMStyYW5kKDApAAAAAwAAAAABP#AAAAAAAAAAAAAGEQAAAAEAAAAAAAAAAD#eTQz86A48AAAADgD#####AAJ5MQALMS4xK3JhbmQoMCkAAAADAAAAAAE#8ZmZmZmZmgAAAAYRAAAAAQAAAAAAAAAAP+#hQopY9IYAAAAOAP####8AAnkyAAsxLjErcmFuZCgwKQAAAAMAAAAAAT#xmZmZmZmaAAAABhEAAAABAAAAAAAAAAA#5J9Nyyx5QAAAAA4A#####wACeTMACzEuMStyYW5kKDApAAAAAwAAAAABP#GZmZmZmZoAAAAGEQAAAAEAAAAAAAAAAD#RvtgjCkF8AAAADgD#####AAJ6MQALMS4yK3JhbmQoMCkAAAADAAAAAAE#8zMzMzMzMwAAAAYRAAAAAQAAAAAAAAAAP+j5izV8TtgAAAAOAP####8AAnoyAAsxLjIrcmFuZCgwKQAAAAMAAAAAAT#zMzMzMzMzAAAABhEAAAABAAAAAAAAAAA#7jiEgUIJrgAAAA4A#####wACejMACzEuMityYW5kKDApAAAAAwAAAAABP#MzMzMzMzMAAAAGEQAAAAEAAAAAAAAAAD#qVqFAND+8AAAADgD#####AAJ0MQALMS4zK3JhbmQoMCkAAAADAAAAAAE#9MzMzMzMzQAAAAYRAAAAAQAAAAAAAAAAP7o#KkKMDIAAAAAOAP####8AAnQyAAsxLjMrcmFuZCgwKQAAAAMAAAAAAT#0zMzMzMzNAAAABhEAAAABAAAAAAAAAAA#1mu2NjNTfAAAAA4A#####wACdDMACzEuMytyYW5kKDApAAAAAwAAAAABP#TMzMzMzM0AAAAGEQAAAAEAAAAAAAAAAD+wy1zsOJ1QAAAADgD#####AARkZWcxAV96ZXJvKGRlcngxKHgxLHkxLHoxLHQxKS1kZXJ4MSh4Mix5Mix6Mix0MikpJnplcm8oZGVyeDEoeDIseTIsejIsdDIpLWRlcngxKHgzLHkzLHozLHQzKSkmemVybyhkZXJ5MSh4MSx5MSx6MSx0MSktZGVyeTEoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcnkxKHgyLHkyLHoyLHQyKS1kZXJ5MSh4Myx5Myx6Myx0MykpJnplcm8oZGVyejEoeDEseTEsejEsdDEpLWRlcnoxKHgyLHkyLHoyLHQyKSkmemVybyhkZXJ6MSh4Mix5Mix6Mix0MiktZGVyejEoeDMseTMsejMsdDMpKSZ6ZXJvKGRlcnQxKHgxLHkxLHoxLHQxKS1kZXJ0MSh4Mix5Mix6Mix0MikpJnplcm8oZGVydDEoeDIseTIsejIsdDIpLWRlcnQxKHgzLHkzLHozLHQzKSkAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCv####8AAAABAA5DQXBwZWxGb25jdGlvbgAAAA0AAAADAQAAAAcAAAAEAAAADgAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAAOAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAAOAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAAA4AAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAABIAAAANAAAAAwEAAAAHAAAABAAAAA8AAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAADwAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAADwAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAPAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAASAAAADQAAAAMBAAAABwAAAAQAAAAQAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABAAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABAAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAEAAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAEQAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAARAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAARAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAABEAAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAAA4A#####wAEZGVnMgFfemVybyhkZXJ4Mih4MSx5MSx6MSx0MSktZGVyeDIoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcngyKHgyLHkyLHoyLHQyKS1kZXJ4Mih4Myx5Myx6Myx0MykpJnplcm8oZGVyeTIoeDEseTEsejEsdDEpLWRlcnkyKHgyLHkyLHoyLHQyKSkmemVybyhkZXJ5Mih4Mix5Mix6Mix0MiktZGVyeTIoeDMseTMsejMsdDMpKSZ6ZXJvKGRlcnoyKHgxLHkxLHoxLHQxKS1kZXJ6Mih4Mix5Mix6Mix0MikpJnplcm8oZGVyejIoeDIseTIsejIsdDIpLWRlcnoyKHgzLHkzLHozLHQzKSkmemVybyhkZXJ0Mih4MSx5MSx6MSx0MSktZGVydDIoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcnQyKHgyLHkyLHoyLHQyKS1kZXJ0Mih4Myx5Myx6Myx0MykpAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAASAAAADQAAAAMBAAAABwAAAAQAAAASAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABIAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABIAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAEgAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAEwAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAATAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAATAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAABMAAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAABIAAAANAAAAAwEAAAAHAAAABAAAABQAAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAAFAAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAFAAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAUAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAASAAAADQAAAAMBAAAABwAAAAQAAAAVAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABUAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABUAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAFQAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAADgD#####AARkZWczAV96ZXJvKGRlcngzKHgxLHkxLHoxLHQxKS1kZXJ4Myh4Mix5Mix6Mix0MikpJnplcm8oZGVyeDMoeDIseTIsejIsdDIpLWRlcngzKHgzLHkzLHozLHQzKSkmemVybyhkZXJ5Myh4MSx5MSx6MSx0MSktZGVyeTMoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcnkzKHgyLHkyLHoyLHQyKS1kZXJ5Myh4Myx5Myx6Myx0MykpJnplcm8oZGVyejMoeDEseTEsejEsdDEpLWRlcnozKHgyLHkyLHoyLHQyKSkmemVybyhkZXJ6Myh4Mix5Mix6Mix0MiktZGVyejMoeDMseTMsejMsdDMpKSZ6ZXJvKGRlcnQzKHgxLHkxLHoxLHQxKS1kZXJ0Myh4Mix5Mix6Mix0MikpJnplcm8oZGVydDMoeDIseTIsejIsdDIpLWRlcnQzKHgzLHkzLHozLHQzKSkAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCgAAABIAAAANAAAAAwEAAAAHAAAABAAAABYAAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAAFgAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAFgAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAWAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAASAAAADQAAAAMBAAAABwAAAAQAAAAXAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABcAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABcAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAFwAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAGAAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAAYAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAAYAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAABgAAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAABIAAAANAAAAAwEAAAAHAAAABAAAABkAAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAAGQAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAGQAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAZAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAAOAP####8ABGRlZzQBX3plcm8oZGVyeDQoeDEseTEsejEsdDEpLWRlcng0KHgyLHkyLHoyLHQyKSkmemVybyhkZXJ4NCh4Mix5Mix6Mix0MiktZGVyeDQoeDMseTMsejMsdDMpKSZ6ZXJvKGRlcnk0KHgxLHkxLHoxLHQxKS1kZXJ5NCh4Mix5Mix6Mix0MikpJnplcm8oZGVyeTQoeDIseTIsejIsdDIpLWRlcnk0KHgzLHkzLHozLHQzKSkmemVybyhkZXJ6NCh4MSx5MSx6MSx0MSktZGVyejQoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcno0KHgyLHkyLHoyLHQyKS1kZXJ6NCh4Myx5Myx6Myx0MykpJnplcm8oZGVydDQoeDEseTEsejEsdDEpLWRlcnQ0KHgyLHkyLHoyLHQyKSkmemVybyhkZXJ0NCh4Mix5Mix6Mix0MiktZGVydDQoeDMseTMsejMsdDMpKQAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAGgAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAAaAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAAaAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAABoAAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAABIAAAANAAAAAwEAAAAHAAAABAAAABsAAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAAGwAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAGwAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAbAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAASAAAADQAAAAMBAAAABwAAAAQAAAAcAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABwAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABwAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAHAAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAHQAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAAdAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAAdAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAAB0AAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAAAIA#####wAEZWdhbAADeD0wAAAAAwgAAAAEAAAAAAAAAAEAAAAAAAAAAAAAAAQAAXgAAXkAAXoAAXT#####AAAAAQAMQ1Rlc3RFcU5hdE9wAP####8AB2VnYWxlcTEAAAABAAAAOAAAABMA#####wAHZWdhbGVxMgAAAAEAAAA4AAAAEwD#####AAdlZ2FsZXEzAAAAAQAAADgAAAATAP####8AB2VnYWxlcTQAAAAEAAAAOAAAAAwA#####wAHc29sZnJhYwAHZnJhYyhYKQAAAAYZAAAADQAAACMAAAAOAP####8AA254MAAMc29sZnJhYygxLDEpAAAADwAAAD0AAAABP#AAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AA2R4MAAMc29sZnJhYygxLDIpAAAADwAAAD0AAAABP#AAAAAAAAAAAAABQAAAAAAAAAAAAAAOAP####8AA255MAAMc29sZnJhYygyLDEpAAAADwAAAD0AAAABQAAAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AA2R5MAAMc29sZnJhYygyLDIpAAAADwAAAD0AAAABQAAAAAAAAAAAAAABQAAAAAAAAAAAAAAOAP####8AA256MAAMc29sZnJhYygzLDEpAAAADwAAAD0AAAABQAgAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AA2R6MAAMc29sZnJhYygzLDIpAAAADwAAAD0AAAABQAgAAAAAAAAAAAABQAAAAAAAAAAAAAAOAP####8AA250MAAMc29sZnJhYyg0LDEpAAAADwAAAD0AAAABQBAAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AA2R0MAAMc29sZnJhYyg0LDIpAAAADwAAAD0AAAABQBAAAAAAAAAAAAABQAAAAAAAAAAAAAAOAP####8AB2NvcnJlY3QAM2RlZzEmZGVnMiZkZWczJmRlZzQmZWdhbGVxMSZlZ2FsZXEyJmVnYWxlcTMmZWdhbGVxNAAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAADQAAADQAAAANAAAANQAAAA0AAAA2AAAADQAAADcAAAANAAAAOQAAAA0AAAA6AAAADQAAADsAAAANAAAAPAAAAA4A#####wAGdW5lc29sAAdkZXRBPD4wAAAAAwkAAAANAAAAIQAAAAEAAAAAAAAAAAAAAAgA#####wAGemVybzE0AA9hYnMoeCk8MTBeKC0xNCkAAAADBAAAAAYAAAAABAAAAAAAAAARAAAAAUAkAAAAAAAAAAAAEAAAAAFALAAAAAAAAAABeAAAAA4A#####wAFZXhhY3QAS3plcm8xNChueDAvZHgwLXgwKSZ6ZXJvMTQobnkwL2R5MC15MCkmemVybzE0KG56MC9kejAtejApJnplcm8xNChudDAvZHQwLXQwKQAAAAMKAAAAAwoAAAADCgAAABIAAABIAAAAAwEAAAADAwAAAA0AAAA+AAAADQAAAD8AAAANAAAAJAAAABIAAABIAAAAAwEAAAADAwAAAA0AAABAAAAADQAAAEEAAAANAAAAJQAAABIAAABIAAAAAwEAAAADAwAAAA0AAABCAAAADQAAAEMAAAANAAAAJgAAABIAAABIAAAAAwEAAAADAwAAAA0AAABEAAAADQAAAEUAAAANAAAAJ#####8AAAACAAZDTGF0ZXgA#####wAAAP8BAAD#####E0AeAAAAAAAAQGsQo9cKPXEBAe#v+wAAAAAAAAAAAAAAAQAAAAAAAAAAAhZcSWZ7Y29ycmVjdH0KewpcSWZ7dW5lc29sfQp7ClxiZWdpbnthcnJheX17bH0KXHRleHR7TGUgc3lzdMOobWUgYWRtZXQgdW4gdW5pcXVlIHF1YWRydXBsZXQgKCR4JDskeSQ7JHokLCR0JCkgc29sdXRpb24gfSAKXFwgXGxlZnQoIFxiZWdpbnthcnJheX17bH0geCBcXCB5XFwgeiBcXCB0IFxlbmR7YXJyYXl9IFxyaWdodClcYXBwcm94IFxsZWZ0KCBcVmFse1gsMTJ9IFxyaWdodCkKXFwgXHRleHR7U29sdXRpb24gcmF0aW9ubmVsbGUgXElme2V4YWN0fXt9e2FwcHJvY2jDqWUgOiB9fQpcbGVmdCggXGJlZ2lue2FycmF5fXtsfSB4IFxcIHlcXCB6IFxcIHQgXGVuZHthcnJheX0gXHJpZ2h0KSBcSWYge2V4YWN0fXs9fXtcYXBwcm94fSBcbGVmdCggXFZhbEZyYWN7WH0gXHJpZ2h0KQpcZW5ke2FycmF5fQp9CnsKXHRleHRjb2xvcntyZWR9e1x0ZXh0e0xlIHN5c3TDqG1lIG4nYSBwYXMgdW5lIHNldWxlIHNvbHV0aW9ufX0KfQoKfQp7Clx0ZXh0Y29sb3J7cmVkfXtcdGV4dHtTeXN0w6htZSBpbmNvcnJlY3Qgb3Ugbm9uIGxpbsOpYWlyZX19Cn3###############8=

Démarrez MathGraph32 (version 6.8.0 ou ultérieure) et utilisez l’icône pour créer une figure sans repère et sans longueur unité.

Nos quatre équations seront contenues dans des fonctions de quatre variables (fonctionnalité disponible seulement depuis la version 6.8.0).

En déroulant la barre d’outils des calculs, cliquez à droite sur l’icône et choisissez Fonction réelle de trois variables ou plus.

Une boîte de dialogue s’ouvre. Remplissez là comme ci-dessous :

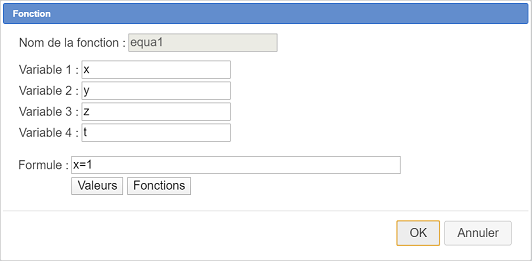
Procédez de même pour créer trois autres fonctions de variables x, y, z et t avec les formules ci-dessous

Nom de la fonction	Formule
equa2	x+y=2
equa3	x+y+z=3
equa4	x+y+z=4-t

Nous pourrons plus tard modifier ces équations mais là nous savons que notre système admet une seule solution $(x ;y ;z ;t)=(1 ;1 ;1 ;1)$

Associons maintenant à ces quatre fonctions des éditeurs de formules qui permettront ensuite de modifier le système à résoudre.

Déroulez la barre des affichages et cliquez sur l’icône .

Cliquez en haut et à gauche de la figure puis remplissez la boîte de dialogue comme ci-dessous :

Procédez de même pour créer 3 autres éditeurs de formules associés aux fonctions equa2, equa3, equa4 en les alignant au-dessous du précédent. Pour déplacer un éditeur, capturez le avec l’outil (la partie active pour la capture est l’intitulé).

Créez de nouveau quatre autres fonctions de variables x, y, z et t avec les formules ci-dessous

Nom de la fonction	Formule
df1	gauche(equa1(x,y,z,t))-droit(equa1(x,y,z,t))
df2	gauche(equa2(x,y,z,t))-droit(equa2(x,y,z,t))
df3	gauche(equa3(x,y,z,t))-droit(equa3(x,y,z,t))
df4	gauche(equa4(x,y,z,t))-droit(equa4(x,y,z,t))

Les opérateurs gauche et droit servent à isoler la partie gauche et droite de l’opérateur d’un calcul (ici l’opérateur sera une égalité).

Déroulez à nouveau la barre d’outils des calculs, cliquez à droite sur l’icône et choisissez Dérivée partielle.

La première dérivée partielle à créer est celle de equa1 par rapport à la variable x.

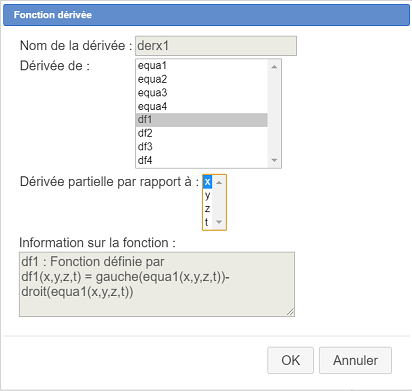
Voici donc les 16 dérivées partielles à créer comme ci-dessous :

Nom de la dérivée partielle	Dérivée de	Variable de dérivation
derx1	df1	x
dery1	df1	y
derz1	df1	z
dert1	df1	t
derx2	df2	x
dery2	df2	y
derz2	df2	z
dert2	df2	t
derx3	df3	x
dery3	df3	y
derz3	df3	z
dert3	df3	t
derx4	df4	x
dery4	df4	y
derz4	df4	z
dert4	df4	t

Nous allons maintenant créer une matrice A de quatre lignes et quatre colonnes.

Pour cela, déroulez à nouveau la barre des outils de calcul, cliquez à droite sur l’icône et choisissez Matrice.

Remplissez la boîte de dialogue comme ci-dessous :

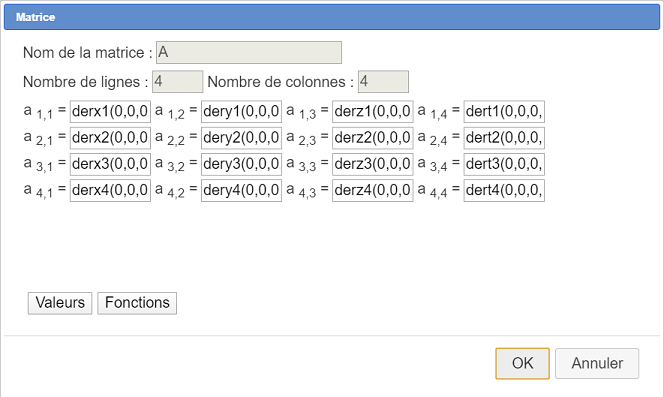
La première formule est par exemple : derx1(0,0,0,0) (puisque derx1 est une fonction de 4 variables puisque dérivée partielle d’une fonction de 4 variables par rapport à x.

Voici les 16 formules pour les 16 éléments de la matrice :

Elément	Formule
$a_{11}$	derx1(0,0,0,0)
$a_{12}$	dery1(0,0,0,0)
$a_{13}$	derz1(0,0,0,0)
$a_{14}$	dert1(0,0,0,0)
$a_{21}$	derx2(0,0,0,0)
$a_{22}$	dery2(0,0,0,0)
$a_{23}$	derz2(0,0,0,0)
$a_{24}$	dert2(0,0,0,0)
$a_{31}$	derx3(0,0,0,0)
$a_{32}$	dery3(0,0,0,0)
$a_{33}$	derz3(0,0,0,0)
$a_{34}$	dert3(0,0,0,0)
$a_{41}$	derx4(0,0,0,0)
$a_{42}$	dery4(0,0,0,0)
$a_{43}$	derz4(0,0,0,0)
$a_{44}$	dert4(0,0,0,0)

Procédez de même pour créer une matrice réelle B à 3 lignes et une colonne comme ci-dessous :

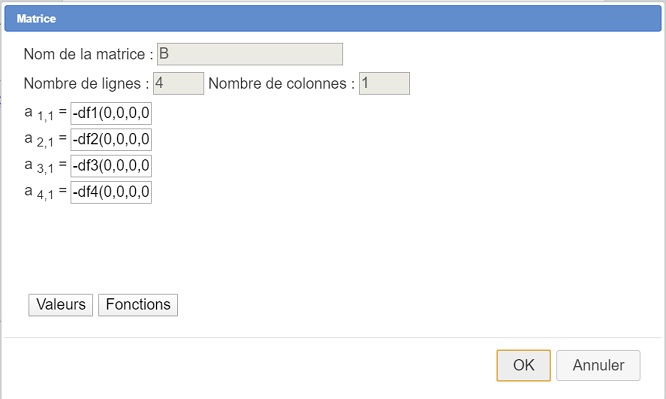
Voici les 4 formules pour les 16 éléments de la matrice :

Elément	Formule
$b_{11}$	-df1(0,0,0,0)
$b_{21}$	-df2(0,0,0,0)
$b_{31}$	-df3(0,0,0,0)
$b_{41}$	-d4(0,0,0,0)

Nous allons maintenant demander le calcul du déterminant de la matrice A qui nous permettra de savoir si le système admet ou pas une unique solution.

Déroulez à nouveau la barre des outils de calcul, cliquez à droite sur l’icône et choisissez Déterminant.

Remplissez la boîte de dialogue comme ci-dessous :

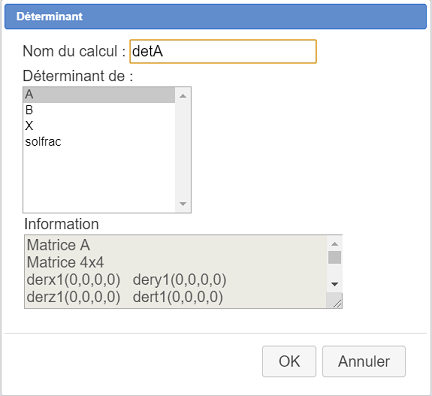
Nous allons maintenant créer un calcul matriciel nommé X contenant la solution de ce système (quand elle est unique).

Déroulez à nouveau la barre des outils de calcul, cliquez à droite sur l’icône et choisissez Calcul matriciel.

Remplissez la boîte de dialogue comme ci-dessous :

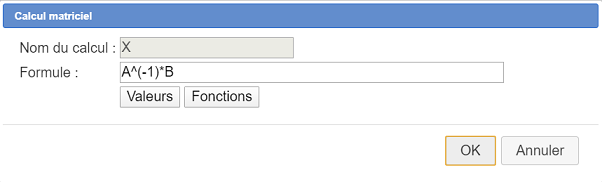
Utilisez maintenant l’icône pour créer les calculs réels suivants :

Nom du calcul	Formule	Commentaire
x0	X(1,1)	Contient la valeur x de la solution unique
y0	X(2,1)	Contient la valeur y de la solution unique
z0	X(3,1)	Contient la valeur z de la solution unique
t0	X(4,1)	Contient la valeur t de la solution unique
x1	1+rand(0)	Valeur aléatoire utilisée pour vérifier que les dérivées partielles sont constantes
x2	1+rand(0)
x3	1+rand(0)
y1	1.1+rand(0)
y2	1.1+rand(0)
y3	1.1+rand(0)
z1	1.2+rand(0)
z2	1.2+rand(0)
z3	1.2+rand(0)
t1	1.3+rand(0)
t2	1.3+rand(0)
t3	1.3+rand(0)

Créez maintenant quatre calculs réels nommés deg1, deg2, deg3 et deg4 avec les formules ci-dessous :

Pour deg1 :

zero(derx1(x1,y1,z1,t1)-derx1(x2,y2,z2,t2))&zero(derx1(x2,y2,z2,t2)-derx1(x3,y3,z3,t3))&zero(dery1(x1,y1,z1,t1)-dery1(x2,y2,z2,t2))&zero(dery1(x2,y2,z2,t2)-dery1(x3,y3,z3,t3))&zero(derz1(x1,y1,z1,t1)-derz1(x2,y2,z2,t2))&zero(derz1(x2,y2,z2,t2)-derz1(x3,y3,z3,t3))&zero(dert1(x1,y1,z1,t1)-dert1(x2,y2,z2,t2))&zero(dert1(x2,y2,z2,t2)-dert1(x3,y3,z3,t3))

Pour deg2 :

zero(derx2(x1,y1,z1,t1)-derx2(x2,y2,z2,t2))&zero(derx2(x2,y2,z2,t2)-derx2(x3,y3,z3,t3))&zero(dery2(x1,y1,z1,t1)-dery2(x2,y2,z2,t2))&zero(dery2(x2,y2,z2,t2)-dery2(x3,y3,z3,t3))&zero(derz2(x1,y1,z1,t1)-derz2(x2,y2,z2,t2))&zero(derz2(x2,y2,z2,t2)-derz2(x3,y3,z3,t3))&zero(dert2(x1,y1,z1,t1)-dert2(x2,y2,z2,t2))&zero(dert2(x2,y2,z2,t2)-dert2(x3,y3,z3,t3))

Pour deg3 :

zero(derx3(x1,y1,z1,t1)-derx3(x2,y2,z2,t2))&zero(derx3(x2,y2,z2,t2)-derx3(x3,y3,z3,t3))&zero(dery3(x1,y1,z1,t1)-dery3(x2,y2,z2,t2))&zero(dery3(x2,y2,z2,t2)-dery3(x3,y3,z3,t3))&zero(derz3(x1,y1,z1,t1)-derz3(x2,y2,z2,t2))&zero(derz3(x2,y2,z2,t2)-derz3(x3,y3,z3,t3))&zero(dert3(x1,y1,z1,t1)-dert3(x2,y2,z2,t2))&zero(dert3(x2,y2,z2,t2)-dert3(x3,y3,z3,t3))

Pour deg4 :

zero(derx4(x1,y1,z1,t1)-derx4(x2,y2,z2,t2))&zero(derx4(x2,y2,z2,t2)-derx4(x3,y3,z3,t3))&zero(dery4(x1,y1,z1,t1)-dery4(x2,y2,z2,t2))&zero(dery4(x2,y2,z2,t2)-dery4(x3,y3,z3,t3))&zero(derz4(x1,y1,z1,t1)-derz4(x2,y2,z2,t2))&zero(derz4(x2,y2,z2,t2)-derz4(x3,y3,z3,t3))&zero(dert4(x1,y1,z1,t1)-dert4(x2,y2,z2,t2))&zero(dert4(x2,y2,z2,t2)-dert4(x3,y3,z3,t3))

Par exemple, deg1 vaudra 1 si l’équation contenue dans equa1 est bien du premier degré par rapport aux variables x, y, z et t.

Nous devons aussi tester si les formules contenues dans les quatre fonctions equa1, equa2, equa3 et equa4 sont bien des égalités.

Pour cela nous allons définir une fonction réelle de quatre variables nommé egal dont la formule soit une égalité.

Créez donc une fonction de quatre variables nommée egal avec comme formule x=0 (n’importe laquelle fonction fait l’affaire du moment qu’elle comprend une égalité).

Déroulez à nouveau la barre des outils de calcul, cliquez à droite sur l’icône et choisissez Test d’équivalence de nature d’opérateur.

Créez le premier test nommé egaleq1 comme ci-dessous :

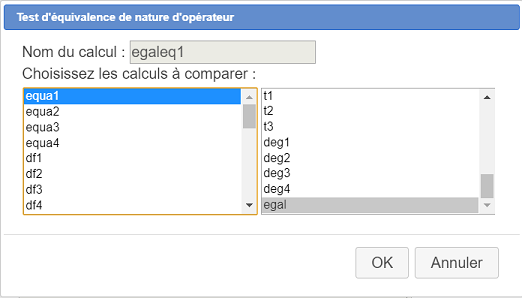
Puis créez de la même façon trois autres tests d’équivalence de nature d’opérateur :

Nom du test de nature d’opérateur	Test entre
egaleq2	equa2 et egal
egaleq3	equa3 et egal
egaleq4	equa4 et egal

Nous allons maintenant créer des solutions rationnelles approchées pour les quatre membres de notre solution (qui n’existe que si elle est unique).

Pour cela nous allons utiliser un calcul matriciel.

Depuis que le calcul matriciel a été introduit dans MathGraph32, une nouvelle fonction frac a été ajoutée que l’on peut utiliser dans les calculs.

Elle peut être appliquée à un nombre, une matrice colonne ou une matrice ligne.

Appliquée à une matrice colonne de n lignes, elle renvoie une matrice de n lignes et deux colonnes. La première colonne du résultat renvoie les numérateurs des valeurs approchées rationnelles de la matrice initiale (à 10^-12 près) et la seconde colonne les dénominateurs.

Déroulez à nouveau la barre des outils de calcul, cliquez à droite sur l’icône et choisissez Calcul matriciel.

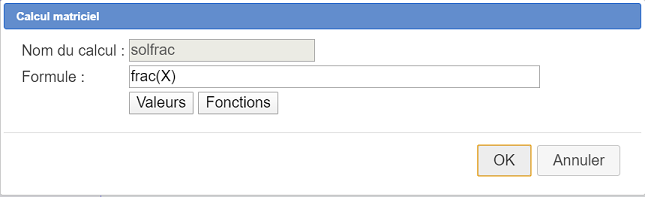
Créez un calcul matriciel nommé solfrac comme ci-dessous :

La formule à utiliser est : frac(X)

Nous allons maintenant récupérer les numérateurs et dénominateurs de ces fractions rationnelles approchées dans des calculs réels.

Créez les calculs réels suivants (outil ) :

Nom du calcul	Formule
nx0	solfrac(1,1)
dx0	solfrac(1,2)
ny0	solfrac(2,1)
dx0	solfrac(2,2)
nz0	solfrac(3,1)
dz0	solfrac(3,2)
nt0	solfrac(4,1)
dt0	solfrac(4,2)
correct	deg1&deg2&deg3&deg4&egaleq1&egaleq2&egaleq3&egaleq4

Le dernier calcul correct prendra pour valeur 1 si le système entré est bien de degré 1 et comporte bien une égalités dans chaque éditeur et 0 sinon.

Créez avec l’icône un calcul réel nommé unesol avec la formule suivante :

detA<>0

unesol vaudra 1 si le système admet bien une unique solution.

Maintenant utilisez l’icône pour créer une fonction réelle de la variable x nommée zero14 définie par la formule suivante :

abs(x)<10^(-14)

Notre solution rationnelle approchée est fournie à 10^(-12) près.

Si l’écart entre celle-ci et notre solution approchée contenue dans (x0, y0, z0, t0) est inférieure à 10^(-14) nous considérerons que la solution rationnelle approchée est exacte.

Utilisez l’icône pour créer un calcul réel nommé exact avec la formule suivante :

zero14(nx0/dx0-x0)&zero14(ny0/dy0-y0)&zero14(nz0/dz0-z0)&zero14(nt0/dt0-t0)

Il nous reste à créer un affichage LaTeX chargé d’afficher la solution quand elle est unique, sinon d’afficher une information si elle n’est pas unique ou si le système n’est pas linéaire.

Dans la barre d’outil des affichages, utilisez l’icône .

Cliquez au-dessous des éditeurs de formules pour désigner l’emplacement de l’affichage LaTeX.

Utilisez le code LaTeX suivant :

\If{correct}
{
\begin{array}{l}
\text{Le système admet un unique quadruplet ($x$;$y$;$z$,$t$) solution } 
\\ \left( \begin{array}{l} x \\ y\\ z \\ t \end{array} \right)\approx \left( \Val{X,12} \right)
\\ \text{Solution rationnelle \If{exact}{}{approchée : }}
\left( \begin{array}{l} x \\ y\\ z \\ t \end{array} \right) \If {exact}{=}{\approx} \left( \ValFrac{X} \right)
\end{array}
}
{
\textcolor{red}{\text{Système incorrect ou non linéaire}}
}

Cet affichage LaTeX comporte des codes d’affichage conditionnels \If spécifiques à MathGraph32.

Rappelons que la syntaxe est \If{condition} {Code LaTeX si condition égal 1}{Code LaTeX sinon}

Le code \Val{X,12} provoque l’affichage de la matrice X, chaque terme arrondi à 12 décimales.

Le code \ValFrac{X} provoque l’affichage de la matrice X où chaque terme est écrit sous forme de fraction rationnelle approchée à 10^(-12) près.

Vous pouvez maintenant modifier les éditeurs de formules pour résoudre le système de votre choix.

Si, par exemple, vous entrez comme première équation x²=1, le système sera déclaré comme non linéaire.

Si vous entrez comme première équation 3x = 1 sans changer les autres équations vous verrez que la solution rationnelle (1/3 ; 5/3 ; 1 ; 1) est déclarée comme exacte.

Mais si vous mettez comme première équation la formule 3x=1.0000000000001 la même solution est déclarée comme approchée.