Toutes les versions de cet article : [Español] [français]
En este artículo, mostraremos cómo usar en una clase una figura para ilustrar un problema de programación lineal. Se recomienda utilizar para ello la versión 4.2.1 de MathGraph32 Java (o posterior).
Queremos ilustrar el siguiente ejercicio :
Un vendedor ambulante ofrece dos categorías de hamburguesas :
– La "simple" : 3 min de preparación, 50 g de guarnición, 0,8 € de ganancia.
– La "maxi" : 5 min de preparación, 150 g de guarnición, 1 € de ganancia.
Para ello, él dispone de 9 kg de guarnición y puede dedicar sólo seis horas al día en su preparación.
Él sabe que no puede pretender vender más de 100 hamburguesas al día.
1) Calcular el tiempo de preparación y la guarnición necesarios para la fabricación de 50 hamburguesas "simples" y 30 hamburguesas "maxis".
Calcular la ganancia obtenida.
2) Se designa con x al número de hamburguesas "simples" y con y el número de hamburguesas "maxis" fabricadas por día (x e y son números enteros positivos).
Escribir las restricciones relativas a x e y como desigualdades.
Representar gráficamente los puntos M(x ; y) del plano que satisfacen estas restricciones.
3) Escribir utilizando x e y la ganancia obtenida B (en €).
4) Para cada real B, se llama $\Delta_B$ la recta de ecuación 0,8x+y = B.
Trazar la recta $\Delta_{70}$ .
5) ¿Cuál es el número de hamburguesas de cada tipo que él debe preparar para obtener la máxima ganancia ?
Desde la versión 4.2 de MathGraph32 es posible trabajar en un referencial (o varios) especificando una unidad sobre cada eje.
Comencemos por crear una figura con un referencial con la ayuda del menú Archivo - Nueva figura con- Referencial sin vectores. Completar la caja de diálogo que se abre como a continuación.
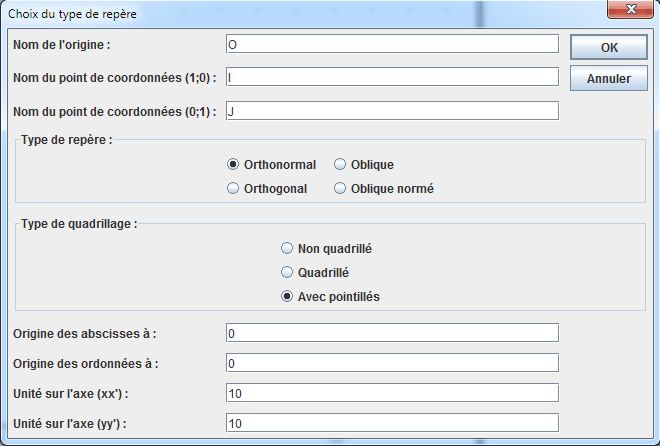
Ampliar un poco la altura de la ventana de esta nueva figura y utilizar la herramienta ![]() para poner el origen O abajo y a la izquierda de la figura y aproximar un poco el punto I al punto O.
para poner el origen O abajo y a la izquierda de la figura y aproximar un poco el punto I al punto O.
Para mejorar la legibilidad vamos a ocultar los nombres de los puntos I y J. Para hacerlo, seleccione la herramienta ![]() y haga clic en el punto y, a continuación, tilde la casilla Nombre oculto .
y haga clic en el punto y, a continuación, tilde la casilla Nombre oculto .
Con la ayuda del ícono ![]() (Atajo teclas Ctrl + Ins) cree los puntos de coordenadas (100 ; 0) y (0 ; 100).
(Atajo teclas Ctrl + Ins) cree los puntos de coordenadas (100 ; 0) y (0 ; 100).
Haga clic en la herramienta ![]() creación de una visualización de LaTeX ligada a un punto y haga clic en el punto I (cuyo nombre está oculto). Introducir 100 en el campo Código LaTeX y validar.
creación de una visualización de LaTeX ligada a un punto y haga clic en el punto I (cuyo nombre está oculto). Introducir 100 en el campo Código LaTeX y validar.
Proceda de manera similar con el punto J.
Recuerde que si desea modificar un objeto gráfico creado por un cuadro de diálogo, como nuestras visualizaciones LaTeX, puede utilizar la herramienta ![]() y haciendo clic sobre el objeto.
y haciendo clic sobre el objeto.
Las restricciones para x y y son las siguientes :
– $x\ge0$
– $y\ge0$
– $3x + 5y\le360$
– $50x +150y\le9000$
– $x+y\le100$
Vamos a representarlas gráficamente.
Comencemos por crear la recta de ecuación $3x + 5y = 360$.
Para ello es suficiente cliquear sobre el ícono ![]() de creación de una recta por una ecuación.
de creación de una recta por una ecuación.
En el cuadro de diálogo que se abre, introduzca 3*x+5*y = 360 en el campo Ecuación. A continuación, utilice el icono ![]() para nombrar esta recta D1.
para nombrar esta recta D1.
Cree de la misma manera las rectas de ecuaciones$50x + 150y = 9000$
y $x + y = 100$. Nomine esas rectas D2 y D3.
Ahora representamos gráficamente los puntos cuyas coordenadas verifican las restricciones.
Para crear un semiplano, necesitamos un punto contenido en él.
Utilice la herramienta ![]() para crear el punto de coordenadas (-5 ; -5).
para crear el punto de coordenadas (-5 ; -5).
Utilice el menú Crear - Superficie - Semiplano y, a continuación, haga clic en el eje de las abscisas y sobre el punto de coordenadas (-5 ; -5).
Oprima la tecla F9 para reactivar la misma herramienta.
Del mismo modo, haga clic sobre el eje de las ordenadas y, a continuación, sobre el punto de coordenadas (-5 ; -5).
Del mismo modo utilice la herramienta ![]() para crear el punto de coordenadas (100 ; 100).
para crear el punto de coordenadas (100 ; 100).
Sobre la paleta de colores, seleccione el color azul.
Utilice el menú Crear - Superficie - Semiplano para crear los semiplanos de bordes D1, D2 y D3 y que contienen este último punto.
Ahora utilizar la herramienta ![]() para ocultar los puntos de coordenadas (-5 ; -5) y (100 ; 100).
para ocultar los puntos de coordenadas (-5 ; -5) y (100 ; 100).
El conjunto de puntos que satisfacen las restricciones es el conjunto de los puntos no sombreadas (incluidos los bordes).
Ahora creamos una función de dos variables correspondiente al beneficio. Para hacer esto use el menú Cálculos - Nuevo cálculo en R - Función real de dos variables. Complete el cuadro de diálogo que aparece a continuación :
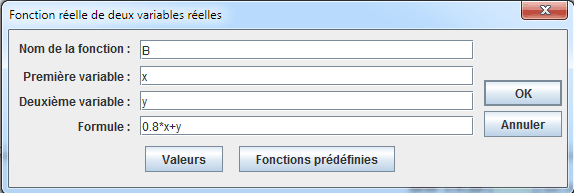
Ahora creamos la recta correspondiente a una ganancia de €70.
Para ello es suficiente activar la herramienta ![]() e introducir como ecuación B(x,y) = 70 (por supuesto también puede introducir 0.8 * x + y = 70).
e introducir como ecuación B(x,y) = 70 (por supuesto también puede introducir 0.8 * x + y = 70).
Con la ayuda de la herramienta ![]() crear un punto ligado a esta recta y luego utilice la herramienta
crear un punto ligado a esta recta y luego utilice la herramienta ![]() para crear una visualización LaTeX ligado a ese punto. Cliquear sobre este punto.
para crear una visualización LaTeX ligado a ese punto. Cliquear sobre este punto.
Complete el cuadro de diálogo como aparece a continuación.
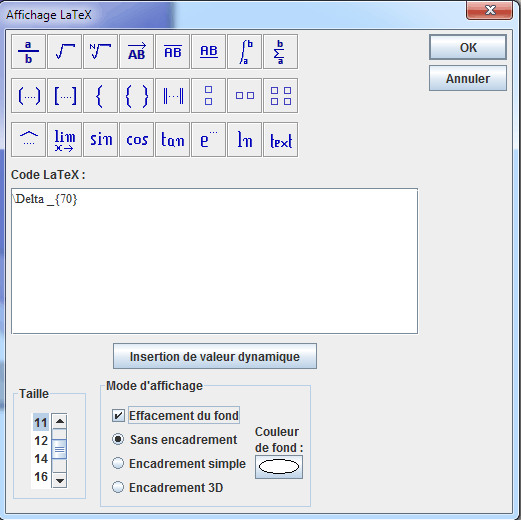
Puede utilizar el botón Griego y cliquear en el carácter $\Delta$ para copiar el código correspondiente a la letra griega.
A continuación, utilice la herramienta ![]() para ocultar el punto ligado.
para ocultar el punto ligado.
Con la ayuda de la herramienta ![]() crear el punto de intersección de la recta D1 con la recta D2 y el punto de intersección de D1 y D3.
crear el punto de intersección de la recta D1 con la recta D2 y el punto de intersección de D1 y D3.
Con la ayuda de la herramienta ![]() crear un punto libre y nombrarlo M (herramienta
crear un punto libre y nombrarlo M (herramienta ![]() ).
).
Ahora vamos a medir la abscisa y la ordenada de M y crear dos cálculos que contengan a esa abscisaa y esa ordenada.
Active la herramienta ![]() de medida de abscisa en un referencial y luego cliquear sobre el punto M. Un mensaje le advierte que esta medida es denotada con xCoord(M,O,I,J).
de medida de abscisa en un referencial y luego cliquear sobre el punto M. Un mensaje le advierte que esta medida es denotada con xCoord(M,O,I,J).
A continuación, utilice la herramienta ![]() de creación de un cálculo. Escriba como nombre xM y utilice el botón Valores para copian en el campo Calculos la abscisa que acaba de ser medida.
de creación de un cálculo. Escriba como nombre xM y utilice el botón Valores para copian en el campo Calculos la abscisa que acaba de ser medida.
De manera similar active la herramienta ![]() de medida de ordenada en un referencial y cliquee sobr4 el punto M. Un mensaje le advierte que esta medida es denotada con yCoord(M,O,I,J).
de medida de ordenada en un referencial y cliquee sobr4 el punto M. Un mensaje le advierte que esta medida es denotada con yCoord(M,O,I,J).
A continuación, utilice la herramienta ![]() para crear un cálculo llamado y M que contiene esta ordenada.
para crear un cálculo llamado y M que contiene esta ordenada.
Utilice el ícono de ![]() para crear los puntos de coordenadas (xM, 0) y (0 ; yM). En la paleta de estilo de trazo, activar el estilo de trazo punteado y unir el punto M a estos dos últimos puntos. Con la ayuda de la herramienta
para crear los puntos de coordenadas (xM, 0) y (0 ; yM). En la paleta de estilo de trazo, activar el estilo de trazo punteado y unir el punto M a estos dos últimos puntos. Con la ayuda de la herramienta ![]() crear una visualización LaTeX ligada al primer punto y como código LaTeX x y una visualización LaTeX ligada all segundo punto y como código LaTeX y.
crear una visualización LaTeX ligada al primer punto y como código LaTeX x y una visualización LaTeX ligada all segundo punto y como código LaTeX y.
Ahora vamos a calcular el beneficio correspondiente a los valores de xM y yM. Para ello utilizar la herramienta ![]() y crear un cálculo llamado Ben que contenga como fórmula B(xM, yM).
y crear un cálculo llamado Ben que contenga como fórmula B(xM, yM).
Creemos ahora en marrón la recta $\Delta_{Ben}}$. Para hacer esto se activa el marrón en la paleta de colores y se utiliza la herramienta ![]() . Se ingresa en el campo de ecuación B(x,y)=Ben (ou 0.8*x+y=Ben). La recta aparece.
. Se ingresa en el campo de ecuación B(x,y)=Ben (ou 0.8*x+y=Ben). La recta aparece.
Siendo Ben la ordenada en elorigen, vamos a crear el punto de coordenadas (0,Ben). Para ello se utiliza la herramienta ![]() y se ingresa 0 en el campo Abscisa y Ben en el campo Ordenada.
y se ingresa 0 en el campo Abscisa y Ben en el campo Ordenada.
Ahora creamos una visualización LaTeX ligada a este último punto que muestre el valor de Ben. Activar la herramienta ![]() y cliquear sobre el punto. En el cuadro de diálogo que se abre, haga clic en el botón Inserción de valor dinámico. En el nuevo cuadro de diálogo, cliquear sobre Ben y elegir 0 como número de decimales. Valide. El contenido del código LaTeX es como se presenta a continuación.
y cliquear sobre el punto. En el cuadro de diálogo que se abre, haga clic en el botón Inserción de valor dinámico. En el nuevo cuadro de diálogo, cliquear sobre Ben y elegir 0 como número de decimales. Valide. El contenido del código LaTeX es como se presenta a continuación.
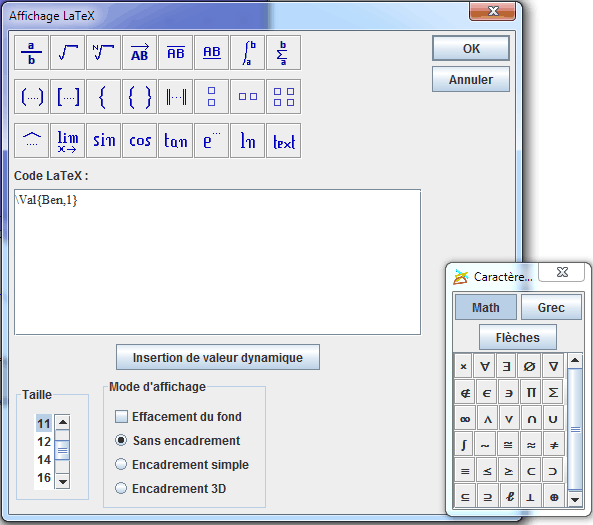
Validar. Puede desplazar la visualización con la herramienta ![]() de captura.
de captura.
Ahora creamos una visualización dinámica para mostrar los valores de xM, yM y Ben en un comentario (visualización de texto) de varios renglones. Utilice para ello la herramienta ![]() .
.
Primero introduzca x_M = y, a continuación, haga clic en Insertar valor dinámico. Un nuevo cuadro de diálogo se visualiza como se muestra a continuación :
Validando se obtiene el código siguiente en la primera línea del comentario : x_M=#Val(xM,1). Encuadre ese código entre dos caracteres $ lo que hará que la visualización se muestre con el estilo LaTeX. El código es entonces $x_M=#Val(xM,1)$.
Oprimir la tecla Enter para pasar de renglón, tipear y_M= y proceder de de la misma manera para obtener el codigo de visualización de yM con un decimal y encuadrarlo entre caracteres $.
Oprimir nuevamente la tecla Enter tipear Ben= y pedir el código para mostrar Ben con un decimal y encuadrarlo entre caracteres $.
Nustra caja de diálogo está finalmente lista. Marcar las casillas Encuadramiento simple y Borado del fondo y validar.
La solución buscada para x y y corresponde a las coordenadas del punto M para el cual la ordenada en el origen de la recta marrón es la más grande, a condición de que M esté en la parte no grisada (incluidos los bordes).
Moviendo el punto M se constata que esa ordenada en el origen parece ser máxima cuando M coincide con el punto de intersección de las rectas D1 y D3.
El punto M es por ahora un punto libre.
Vamos a pedirle al software transformar en punto ligado a un otro punto.
Utilice para ello el menú Edición - Creación de una ligadura - Entre un punto y un objeto luego haga clic en el punto M y a continuación sobre el punto de intersección de D1 y D3. Vemos que para esa posición de M la ganancia o beneficio es máxima y que ella es de 86 para xM = 70 y yM = 30.
Nuestro beneficio será entonces máximo para 70 hamburguesas "simples" y 30 "maxis".
La siguiente es la figura obtenida antes de ligar el punto M y el punto de intersección (se puede capturar M) :
Y la figura final :
Con un poco más trabajo y utilizando macros de Aparición de objetos y de Ocultamiento de objetos puede obtenerse la figura siguiente (haga clic en ejecutar las macros) :
Puede descargar las tres figuras anteriores en un archivo zipeado :