Toutes les versions de cet article : [English] [Español] [français]
Cet article a été revu pour être adapté à la version JavaScript de MathGraph32 et va montrer comment utiliser une macro construction de façon itérative. Utilisez de préférence la version 7.3.5 de MathGraph32 ou une version ultérieure.
Nous allons commencer par créer une construction que nous implémenterons ensuite de façon itérative dans une autre figure.
Commencez par utiliser l’icône  de la barre supérieure et demandez la création d’une figure munie d’un repère.
de la barre supérieure et demandez la création d’une figure munie d’un repère.
Utilisez ensuite l’icône  pour créer une fonction nommée f avec comme variable formelle x et comme formule x^2. Laissez la case Tracer courbe cochée.
pour créer une fonction nommée f avec comme variable formelle x et comme formule x^2. Laissez la case Tracer courbe cochée.
Maintenant utilisez l’icône  pour créer un calcul nommé a contenant comme formule 1.5.
pour créer un calcul nommé a contenant comme formule 1.5.
Les trois objets sources de notre construction seront le repère (O ;I,J), la fonction f et le calcul a. Nos objets finaux ne doivent donc dépendre que de ces trois objets. Cela nous interdit par exemple d’utiliser la droite (OI) car le repère a été défini à l’aide des points O et I. Utilisez donc l’outil  pour masquer l’axe des abscisses.
pour masquer l’axe des abscisses.
Maintenant utilisez l’icône  pour créer un point de coordonnées (0 ; 0) et un point de coordonnées (1 ; 0) puis l’icône
pour créer un point de coordonnées (0 ; 0) et un point de coordonnées (1 ; 0) puis l’icône  pour joindre ces deux points par une droite (choisir les points par coordonnées dans la boîte de dialogue de choix du type d’objet qui s’ouvre lorsque vous cliquez sur un point).
pour joindre ces deux points par une droite (choisir les points par coordonnées dans la boîte de dialogue de choix du type d’objet qui s’ouvre lorsque vous cliquez sur un point).
Dans la palette de style de trait, activez le style de trait pointillé.
En déroulant la barre d’outils des droites, utilisez l’icône  pour créer la tangente à la courbe au point d’abscisse a comme ci-dessous :
pour créer la tangente à la courbe au point d’abscisse a comme ci-dessous :
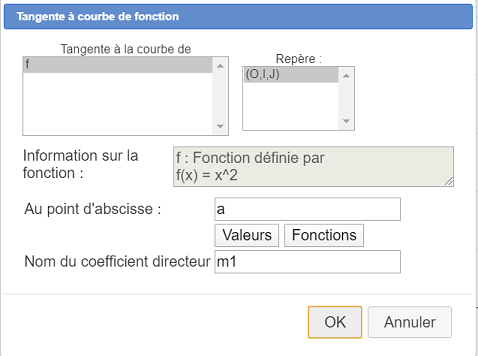
Puis, en déroulant la barre d’outil des points, utilisez l’icône  pour créer l’intersection de cette tangente avec la droite passant par les points de coordonnées (0 ; 0) et (1 ;0) que nous avons créée précédemment.
pour créer l’intersection de cette tangente avec la droite passant par les points de coordonnées (0 ; 0) et (1 ;0) que nous avons créée précédemment.
Utilisez l’outil  de la barre supérieure pour nommer le point créé A en cochant la case Nom masque.
de la barre supérieure pour nommer le point créé A en cochant la case Nom masque.
Utilisez maintenant l’icône  pour mesurer l’abscisse du point A dans le repère. Une boîte de dialogue s’ouvre pour vous demander de choisir un nom pour cette abscisse. Entrez x comme nom et validez.
pour mesurer l’abscisse du point A dans le repère. Une boîte de dialogue s’ouvre pour vous demander de choisir un nom pour cette abscisse. Entrez x comme nom et validez.
Les deux premiers objets sources (le repère et la fonction) seront communs à toutes les implémentations de la construction mais le troisième (le calcul a) sera remplacé à chaque itération par le premier des objets finaux numériques, à savoir le calcul x.
Comme les objets sources numériques sont toujours choisis en premier et comme notre construction devra se réappliquer à elle même, les autres objets finaux doivent être définis après le calcul x.
Nous allons donc créer des clones d’objets.
Tout en bas de la barre d’outils verticale, cliquez sur l’icône  et choisissez l’item Clone d’objet. Cliquez sur le point A pour créer un clone de ce point.
et choisissez l’item Clone d’objet. Cliquez sur le point A pour créer un clone de ce point.
Recommencez le même processus mais cette fois en cliquant sur la tangente pour créer un clone de cette droite.
Utilisez l’icône  pour créer un point de coordonnées (a ; 0) et un autre point de coordonnées (a ; f(a)).
pour créer un point de coordonnées (a ; 0) et un autre point de coordonnées (a ; f(a)).
Dans la palette de style de trait, activez le style de trait pointillé puis joignez ces deux points par un segment pointillé avec l’icône  .
.
Notre figure est prête pour définir notre construction.
Commencez par cliquer dans la barre supérieure sur l’icône  qui fait apparaître des outils supplémentaires.
qui fait apparaître des outils supplémentaires.
Cliquez sur l’icône  (création d’une construction) et choisissez l’item Choix des objets sources numériques.
(création d’une construction) et choisissez l’item Choix des objets sources numériques.
Une boîte de dialogue s’ouvre. Dans la liste de gauche , faites un double clic successif sur (0 ;I,J), f et a (ou utilisez le bouton Insérer) comme ci-dessous :
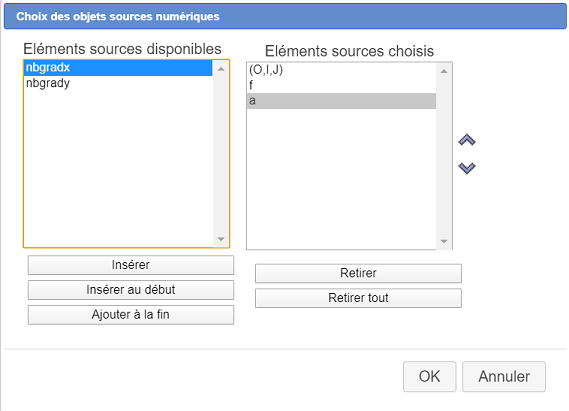
Commençons par définir les objets finaux numériques : Il n’y en a qu’un qui est le calcul x.
Cliquez à nouveau sur l’icône  (création d’une construction) et choisissez l’item Choix des objets finaux numériques.
(création d’une construction) et choisissez l’item Choix des objets finaux numériques.
Remplissez la boîte de dialogue comme ci-dessous (il suffit de cliquer sur un élément de la liste pour sélectionner ou désélectionner).
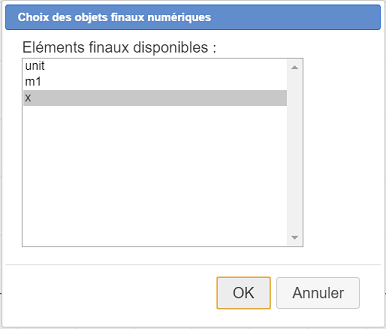
Cliquez à nouveau sur l’icône  (création d’une construction) et choisissez l’item Choix des objets finaux graphiques.
(création d’une construction) et choisissez l’item Choix des objets finaux graphiques.
Cliquez sur : le clone du point A, le clone de la tangente, le point de coordonnées (a ; 0), le point de coordonnées (a ; f(a)) et le segment qui les joint. Puis cliquez en bas et à droite de la fenêtre sur le bouton rouge  pour indiquer que tous les objets finaux graphiques ont été choisis.
pour indiquer que tous les objets finaux graphiques ont été choisis.
Il reste à finaliser notre construction (elle n’a pas d’objet source graphique).
Cliquez à nouveau sur l’icône  et choisissez l’item Finir la construction en cours et remplissez la boîte de dialogue comme ci-dessous :
et choisissez l’item Finir la construction en cours et remplissez la boîte de dialogue comme ci-dessous :
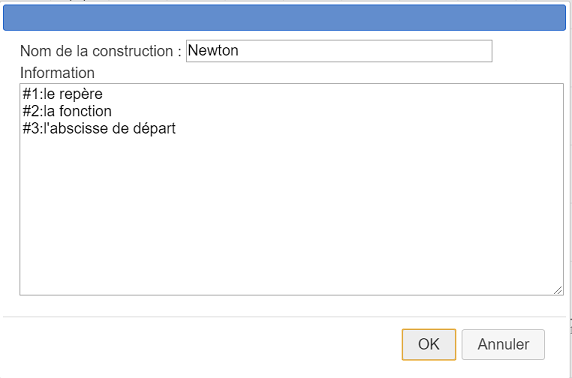
Voici le contenu de l’éditeur Information :
Chacune des 3 lignes ci-dessus sera utilisée pour donner une information lorsque l’utilisateur implémentera la construction.
Maintenant sauvegardez votre figure dans le dossier de votre choix (la construction est incluse dans la figure).
Nous allons aussi sauvegarder notre construction dans un fichier séparé (de suffixe mgc).
Pour cela utilisez l’icône  et choisissez l’item Enregistrer une construction de la figure.
et choisissez l’item Enregistrer une construction de la figure.
Une boîte de dialogue s’ouvre. Dans la liste, la construction Newton est déjà sélectionnée.
Cliquez sur le bouton Enregistrer et enregistrez la macro construction dans le dossier de votre choix (il est conseillé de garder le même nom pour le fichier que la construction, le fichier généré sera donc Newton.mgc).
Voici ci-dessous la figure obtenue en mode édition :
Maintenant nous allons créer une nouvelle figure dans laquelle nous implémenterons notre construction de façon itérative.
Utilisez l’icône  et créez une figure munie d’un repère orthogonal.
et créez une figure munie d’un repère orthogonal.
Utilisez l’icône  et choisissez l’item Incorporer une construction depuis un fichier.
et choisissez l’item Incorporer une construction depuis un fichier.
Une boîte de dialogue de choix de fichier s’ouvre. Allez dans le dossier contenant la macro construction que vous avez enregistrée précédemment et cliquez sur le bouton Ouvrir.
La construction Newton fait maintenant partie de votre figure.
Utilisez l’icône  pour créer une fonction nommée f avec comme variable formelle x et comme formule par exemple :
pour créer une fonction nommée f avec comme variable formelle x et comme formule par exemple :
Laissez cochée la case Tracer Courbe et validez.
Créez maintenant l’icône  pour créer un point lié à l’axe des abscisses et nommez ce point M.
pour créer un point lié à l’axe des abscisses et nommez ce point M.
Déroulez la barre d’outil des mesures et utilisez l’outil  pour mesurer l’abscisse du point M dans le repère (O ; I, J). Une boîte de dialogue vous demande le nom de cette mesure : entrez xM par exemple.
pour mesurer l’abscisse du point M dans le repère (O ; I, J). Une boîte de dialogue vous demande le nom de cette mesure : entrez xM par exemple.
Déroulez la barre d’outils des affichages et, à sa droite, cliquez sur l’icône  . Choisissez l’item Macro de construction itérative et remplissez la boîte de dialogue comme ci-dessous.
. Choisissez l’item Macro de construction itérative et remplissez la boîte de dialogue comme ci-dessous.
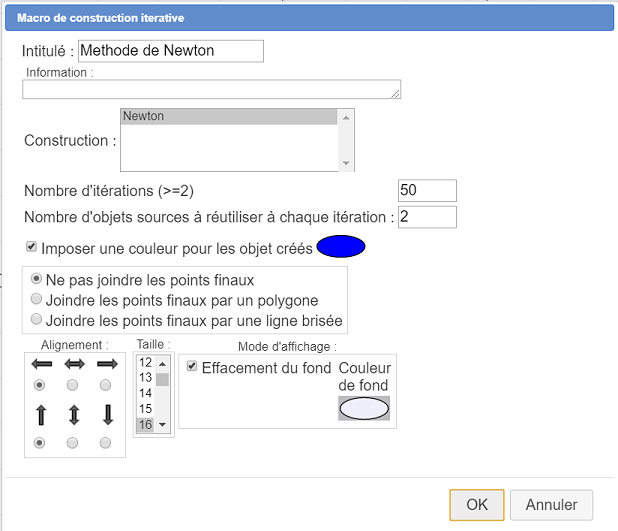
Puis une autre boîte de dialogue demande de choisir les objets sources numériques.
Les deux premiers seront communs à toutes les itérations. Le troisième (valeur de départ pour la suite) sera remplacé par le calcul x à chaque itération. Remplissez la boîte de dialogue en affectant à l’élément source 1 le repère, à l’élément source n°2 la fonction f et à l’élément source n°3 l’abscisse xM comme ci-dessous.
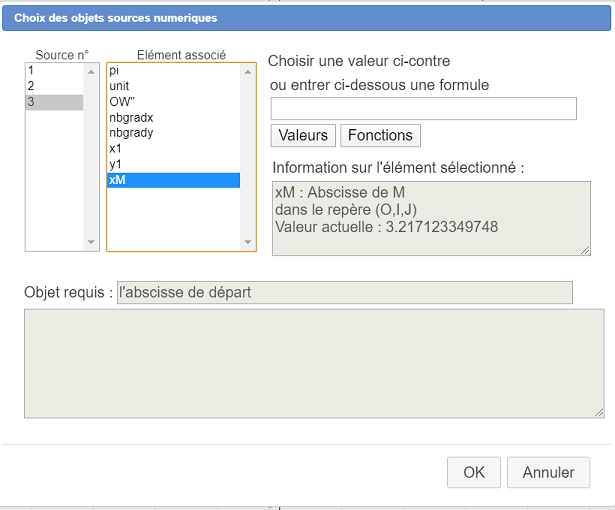
La macro apparaît.
Créons un éditeur de formule qui permettra de modifier la formule de la fonction f directement sur la figure.
Pour cela, déroulez la barre d’outil des affichages et utilisez l’icône  . Cliquez en haut et à gauche de la figure (sous la macro Méthode de Newton).
. Cliquez en haut et à gauche de la figure (sous la macro Méthode de Newton).
Remplissez la boîte de dialogue comme ci-dessous :
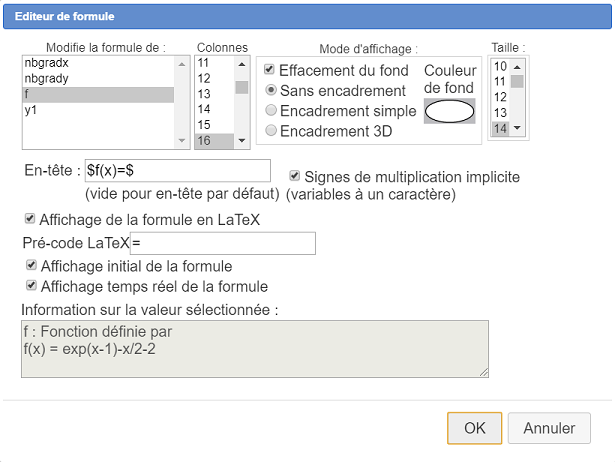
Vous pouvez déplacer cet éditeur de formule avec l’outil de capture  (capturer ce qui est à gauche de l’éditeur).
(capturer ce qui est à gauche de l’éditeur).
Si nous exécutons notre macro et enregistrons la figure, elle contiendra de nombreux objets.
Nous allons demander à ce que notre macro de construction itérative soit exécutée dès le chargement de la figure.
Pour cela, dans la barre d’outils supérieure, cliquez sur l’icône  et cliquez en bas sur Choix d’une macro pour le démarrage.
et cliquez en bas sur Choix d’une macro pour le démarrage.
Dans la liste cliquez sur la macro Méthode de Newton et validez.
Sauvegardez votre figure dans le dossier de votre choix.
A la prochaine ouverture de cette figure la macro sera exécutée automatiquement comme c’est le cas pour la figure ci-dessous.
Puis exécutez la macro avec l’outil  .
.
En utilisant l’outil  de la barre d’outils supérieure, vous pouvez maintenant voir que de nombreux nouveaux objets ont été rajoutés à la figure.
de la barre d’outils supérieure, vous pouvez maintenant voir que de nombreux nouveaux objets ont été rajoutés à la figure.
Voici le code Base64 de la figure avec démarrage automatique :
En cliquant sur l’icône  vous verrez que la figure contient maintenant des calculs nommés xa1, xa2, ..., xa50 qui sont en fait les cinquante premiers termes de la suite formée des abscisses des points d’intersection des tangentes avec l’axe des abscisses.
vous verrez que la figure contient maintenant des calculs nommés xa1, xa2, ..., xa50 qui sont en fait les cinquante premiers termes de la suite formée des abscisses des points d’intersection des tangentes avec l’axe des abscisses.
Vous pouvez maintenant capturer le point M pour visualiser la rapidité de convergence suivant le premier terme comme ci-dessous et changer la formule de f(x).
Ci-dessous une figure plus sophistiquée où on fait afficher les termes successifs de la suite formée des abscisses des points d’intersection des tangentes avec l’axe des abscisses (on se sert pour cela d’une suite récurrente).
Cliquez en bas et à droite sur les boutons + ou - pour voir la valeur des termes de cette suite.
Vous pouvez étudier la façon dont cette figure est créé (figure en mode édition).