Toutes les versions de cet article : [English] [Español] [français]
Cet article a été remanié et adapté à la version JavaScript de MathGraph32. Il montre comment créer une construction permettant de créer automatiquement l’image d’une cercle par une transformation complexe donnée.
Créez une nouvelle figure à l’aide de l’icône  et choisissez de créer une figure avec un repère orthonormal.
et choisissez de créer une figure avec un repère orthonormal.
Utilisez l’icône  pour créer deux points libres puis l’icône
pour créer deux points libres puis l’icône  pour créer le cercle de centre un des deux points et passant par l’autre.
pour créer le cercle de centre un des deux points et passant par l’autre.
A l’aide de l’icône  créez un point lié à ce cercle et nommez-le M .
créez un point lié à ce cercle et nommez-le M .
Déroulez la barre d’icônes des mesures et utilisez l’icône  pour créer la mesure de l’affixe du point M dans notre repère en cliquant sur le point M. Choisissez comme nom z pour cette mesure.
pour créer la mesure de l’affixe du point M dans notre repère en cliquant sur le point M. Choisissez comme nom z pour cette mesure.
Déroulez la barre d’outils des calculs et utilisez l’icône 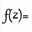 pour créer une fonction complexe nommée f définie par f(t) = t+1/t.
pour créer une fonction complexe nommée f définie par f(t) = t+1/t.
L’icône 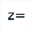 va vous permettre de créer un calcul complexe nommé z’ contenant comme formule f(z).
va vous permettre de créer un calcul complexe nommé z’ contenant comme formule f(z).
Créez maintenant le point d’affixe z’ à l’aide de l’icône  . Nommez ce nouveau point M’.
. Nommez ce nouveau point M’.
Nous allons maintenant créer le lieu du point M’ généré par les positions du point M sur le cercle auquel il est lié.
Dans la palette des couleurs activez la couleur rouge.
Pour cela utilisons l’icône  (lieu de points généré par point lié). Il vous est demandé d’abord de cliquer sur le point dont les traces généreront le lieu : cliquez sur M’. Il vous est ensuite demandé de cliquer sur le point lié dont les positions généreront le lieu : cliquez sur M. Une boîte de dialogue s’ouvre alors. Demandez 500 points et cochez la case Lieu fermé puis validez. Le lieu apparaît.
(lieu de points généré par point lié). Il vous est demandé d’abord de cliquer sur le point dont les traces généreront le lieu : cliquez sur M’. Il vous est ensuite demandé de cliquer sur le point lié dont les positions généreront le lieu : cliquez sur M. Une boîte de dialogue s’ouvre alors. Demandez 500 points et cochez la case Lieu fermé puis validez. Le lieu apparaît.
Le moment est venu de créer notre construction.
Dans la barre d’outils du haut, cliquez sur l’icône  qui fait apparaître des icônes supplémentaires.
qui fait apparaître des icônes supplémentaires.
Il nous faut d’abord indiquer les objets sources de notre construction.
Commençons par les objets sources numériques.
Utilisez l’icône  (création de construction) et cliquez sur Choix des objets sources numériques.
(création de construction) et cliquez sur Choix des objets sources numériques.
Une boîte de dialogue apparaît. Nos deux éléments sources numériques sont la fonction f et le repère (O,I,J)
Cliquez sur le repère (O,I,J) (ou double-cliquez sur le repère) comme ci-dessous) puis faites de même avec la fonction f.
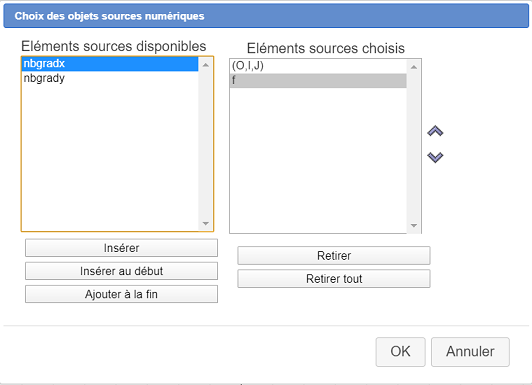
Il nous faut maintenant choisir nos éléments sources graphiques. Pour cela utilisez à nouveau l’icône  et choisissez Choix des objets sources graphiques. Cliquez sur le cercle puis cliquez sur le bouton rouge STOP pour indiquer que vous avez fini .
et choisissez Choix des objets sources graphiques. Cliquez sur le cercle puis cliquez sur le bouton rouge STOP pour indiquer que vous avez fini .
Choisissons les éléments finaux de notre construction en commençant par les objets finaux graphiques.
Utilisez l’icône  et cliquez sur Choix des objets finaux graphiques.
et cliquez sur Choix des objets finaux graphiques.
Vous ne pouvez cliquer que sur des objets créés exclusivement avec les objets sources. Cliquez sur M, sur M’ et sur le lieu de points. En bas et à droite cliquez sur le bouton rouge STOP pour indiquer que vous avez fini de désigner les objets finaux graphiques.
Choisissons maintenant les objets finaux numériques.
Pour cela utilisez à nouveau l’icône  et choisissez Choix des objets finaux numériques.
et choisissez Choix des objets finaux numériques.
Cliquez sur z, z’ comme ci-dessous.
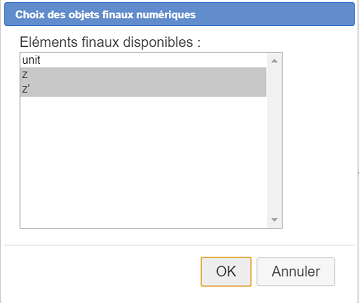
Il nous reste à finaliser notre construction et l’enregistrer.
Utilisez à nouveau l’icône  et choisissez Finir la construction en cours.
et choisissez Finir la construction en cours.
Renseignez la boîte de dialogue qui s’ouvre comme ci-dessous :
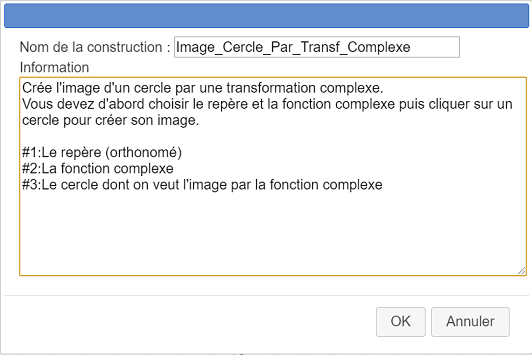
Voici le texte du commentaire :
Crée l'image d'un cercle par une transformation complexe.
Vous devez d'abord choisir le repère et la fonction complexe puis cliquer sur un cercle pour créer son image.
#1:Le repère (orthonomé)
#2:La fonction complexe
#3:Le cercle dont on veut l'image par la fonction complexeLes trois dernières lignes donnent des informations qui seront affichées lorsque l’utilisateur est amené à choisir l’objet correspondant à l’objet source.
Enregistrez maintenant votre construction sur votre disque dans le répertoire de votre choix en utilisant l’icône  puis en cliquant sur Enregistrer une construction de la figure (il est conseillé de garder pour le fichier le même nom que celui de la construction, ou un nom voisin évocateur).
puis en cliquant sur Enregistrer une construction de la figure (il est conseillé de garder pour le fichier le même nom que celui de la construction, ou un nom voisin évocateur).
Nous allons maintenant montrer comment utiliser notre construction dans une autre figure.
Utilisez l’icône  et demandez un repère orthonormal puis dans la boîte de dialogue, cochez en bas la case Avec vecteurs . Utilisez l’outil de capture pour éloigner le point d’abscisse 1 sur l’axe des abscisses de l’origine du repère.
et demandez un repère orthonormal puis dans la boîte de dialogue, cochez en bas la case Avec vecteurs . Utilisez l’outil de capture pour éloigner le point d’abscisse 1 sur l’axe des abscisses de l’origine du repère.
Utilisez l’icône 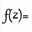 pour créer une fonction complexe nommée f définie par f(t) = t+1/t^2.
pour créer une fonction complexe nommée f définie par f(t) = t+1/t^2.
A l’aide de l’outil
Utilisons notre construction : Utilisez l’icône  (gestion des constructions) et choisissez l’item Incorporer une construction depuis un fichier. Une boîte de dialogue s’ouvre. Ouvrez le dossier contenant la construction que vous venez d’enregistrer, cliquez sur son nom puis sur Ouvrir.
(gestion des constructions) et choisissez l’item Incorporer une construction depuis un fichier. Une boîte de dialogue s’ouvre. Ouvrez le dossier contenant la construction que vous venez d’enregistrer, cliquez sur son nom puis sur Ouvrir.
La construction fait maintenant partie de la figure.
Il faut maintenant l’implémenter.
Utilisez de nouveau l’icône  et choisissez l’item Implémenter une construction de la figure.
et choisissez l’item Implémenter une construction de la figure.
Une boîte de dialogue s’ouvre vous présentant la seule construction de la figure qui est déjà sélectionnée. Cliquez sur le bouton Implémenter.
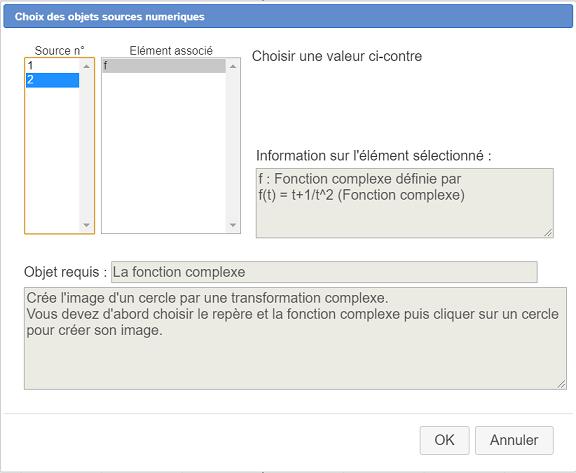
Une nouvelle boîte de dialogue s’ouvre pour choisir les éléments sources numériques. Comme objet source numéro 1, le repère (O,I,J) est déjà sélectionné.
Dans la liste de gauche, cliquez sur le numéro 2. Dans la liste de droite, sélectionnez la fonction f comme ci-dessous. Validez.
.
En haut et à droite apparaît l’indication que nous avons prévue pour l’objet source numéro 3 (le cercle).
Cliquez sur le cercle.
L’image du cercle par notre transformation complexe f apparaît. Elle a été créée par la macro construction. En capturant le point lié à l’axe des abscisses par lequel passe le cercle elle est actualisée automatiquement.
Vous pouvez aussi capturer le point lié M qui a été créé par la macro-construction et voir varier son image M’.
En cliquant sur l’icône  vous verrez que des éléments finaux de type calcul sont disponibles nommés z et z’ qui sont les affixes du point lié au cercle et de son image.
vous verrez que des éléments finaux de type calcul sont disponibles nommés z et z’ qui sont les affixes du point lié au cercle et de son image.
Pour finir nous allons créer un éditeur de formule qui permettra de changer la formule de la fonction complexe f directement sur la figure.
Pour cela utilisez l’icône  en déroulant la barre d’outil des affichages.
en déroulant la barre d’outil des affichages.
Cliquez en haut et à gauche de la figure puis renseignez la boîte de dialogue comme ci-dessous :
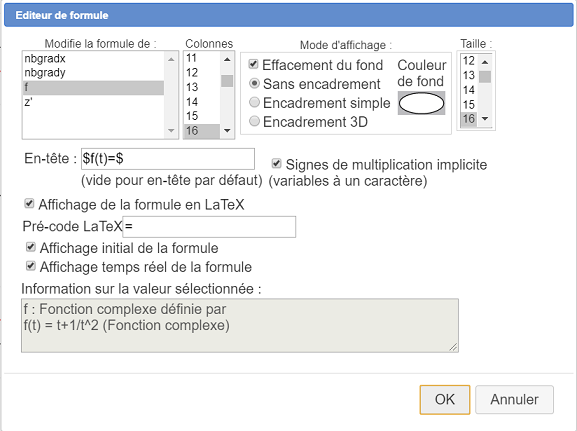
Vous pouvez déplacer cet éditeur de formule à l’aide de l’outil de capture ( ) en cliquant sur son intitulé à gauche.
) en cliquant sur son intitulé à gauche.
Le fait d’utiliser des $ en début et fin du champ En-tête fait que l’en-tête est écrit en LaTeX.
Voici ci-dessous la figure obtenue animée par MathGraph32 en ligne.
Vous pouvez y modifier la formule de f.
Essayez par exemple la formule $f(t)=1/2*\left(t+\frac{1}{t}\right)$