Toutes les versions de cet article : [Español] [français]
Un colega (gracias Thomas) me hizo conocer este vídeo : https://www.youtube.com/watch?v=-X49VQgi86E, entonces tuve la idea de hacer una figura dinámica para ilustrar estos resultados.
La idea es la siguiente, n y p son números naturales mayores o iguales a 2 :
Representamos cada uno de los números naturales k entre 0 y n - 1 mediante puntos regularmente espaciados en una circunferencia.
Para cada número natural k entre 0 y n - 1, conectamos por un segmento el punto asociado a k y el punto asociado con $k \times p$.
Haremos esta figura con la nueva versión de JavaScript de MathGraph32 que se puede descargar en esta página o utilizar en línea en esta página.
Inicie el software y use el icono ![]() que permite crear una nueva figura. Elija una figura sin referencial y sin longitud de unidad (para este tipo de figura, la unidad de ángulo es el grado).
que permite crear una nueva figura. Elija una figura sin referencial y sin longitud de unidad (para este tipo de figura, la unidad de ángulo es el grado).
Utilice la herramienta ![]() , para crear un punto libre al que llamaremos O (ingrese el nombre en el editor que aparece sobre la figura una vez creado el punto).
, para crear un punto libre al que llamaremos O (ingrese el nombre en el editor que aparece sobre la figura una vez creado el punto).
Use el icono ![]() para crear una recta vertical que pase por el punto 0. Para usar esta herramienta, debe desarrollar la segunda barra de iconos desde la parte superior (haciendo doble clic sobre el icono visible o haciendo clic sobre la flecha amarilla), haga clic en el icono
para crear una recta vertical que pase por el punto 0. Para usar esta herramienta, debe desarrollar la segunda barra de iconos desde la parte superior (haciendo doble clic sobre el icono visible o haciendo clic sobre la flecha amarilla), haga clic en el icono ![]() y haga clic en el punto O.
y haga clic en el punto O.
Usando la herramienta ![]() (primera fila de iconos), cree un punto ligado a esta recta vertical que llamaremos I.
(primera fila de iconos), cree un punto ligado a esta recta vertical que llamaremos I.
Utilice el icono ![]() para crear la circunferencia de centro O y que pasa por I.
para crear la circunferencia de centro O y que pasa por I.
Ahora crearemos dos variables n y p.
La creación de objetos numéricos se realiza en la tercera barra de herramientas a partir de abajo.
Utilice el icono ![]() y complete el cuadro de diálogo como se muestra a continuación (no olvide de marcar la casilla Diálogo asociado) :
y complete el cuadro de diálogo como se muestra a continuación (no olvide de marcar la casilla Diálogo asociado) :
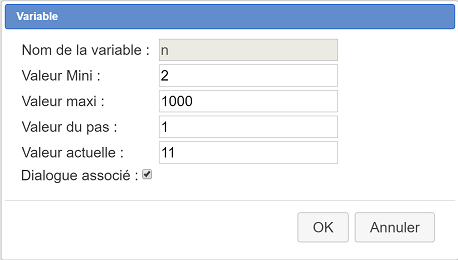
Notará que apareció un pequeño cuadro de diálogo en la parte inferior derecha de la ventana. Él permite aumentar o disminuir la variable n o modificarla.
Del mismo modo, cree una variable p como se muestra a continuación :
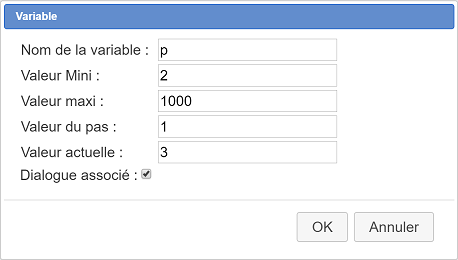
Ahora crearemos una función f que, a un natural x, le asocia el ángulo de rotación del centro O asociando al punto I el punto que representa el natural x en nuestra circunferencia.
Para ello utilice el icono ![]() situado en la tercera fila de iconos de la parte inferior y complete el cuadro de diálogo de la siguiente manera :
situado en la tercera fila de iconos de la parte inferior y complete el cuadro de diálogo de la siguiente manera :
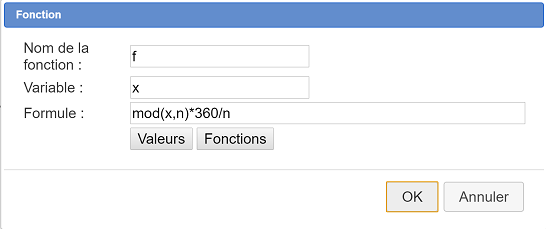
Aquí está la fórmula de la función : mod(x,n)*360/n
La función mod(x, n) devuelve el resto de la división euclidiana de x por el número entero n (x debe ser un número entero positivo o cero y n un número entero positivo).
Ahora necesitamos crear lugares de objetos cuyo número de objetos será el valor de n. Como una variable no puede depender de otra variable, utilizaremos los lugares de objetos generados por un punto ligado.
Para este punto ligado usaremos un cursor. No podemos usar un cursor entero porque este tipo de cursor no puede generar un lugar.
Use el ícono ![]() para crear un cursor y elija un cursor grande de la siguiente manera :
para crear un cursor y elija un cursor grande de la siguiente manera :
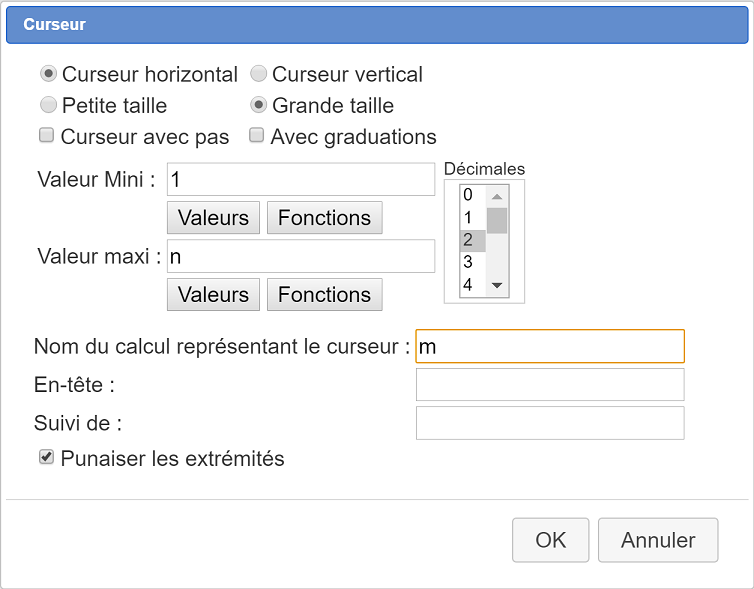
Los valores tomados por nuestro cursor están en un cálculo llamado m pero este cálculo no toma valores enteros.
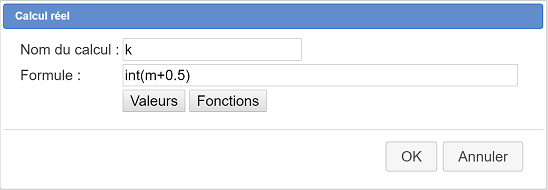
Por lo tanto, utilizaremos el icono ![]() para crear un cálculo llamado k que tomará el valor entero más cercano a m. Complete el cuadro de diálogo de la siguiente manera :
para crear un cálculo llamado k que tomará el valor entero más cercano a m. Complete el cuadro de diálogo de la siguiente manera :
En la paleta de colores active el color rojo.
En la barra de iconos asociada a las transformaciones (que es por defecto el de la traslación) active el icono ![]() de la rotación.
de la rotación.
Haga clic en el punto O.
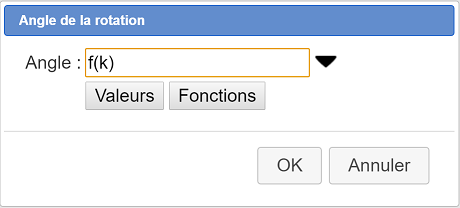
Se abre un cuadro de diálogo para pedirle el ángulo que se muestra a continuación. Ingrese el ángulo f(k) como se muestra a continuación :
Luego haga clic sobre el punto I para crear su punto imagen. Nombre a este punto A.
Ahora crearemos el punto asociado con al entero $k \times p$
Haga clic nuevamente sobre el icono![]() y haga clic sobre el punto O.
y haga clic sobre el punto O.
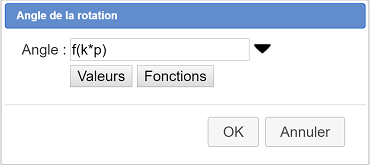
Esta vez ingrese como el ángulo de rotación f(k*p) como se muestra a continuación :
Nombre a este punto B.
Una los puntos A y B por un segmento con la herramienta ![]()
Al capturar con la herramienta ![]() el punto de móvil del cursor se puede ver que el segmento [AB] varía.
el punto de móvil del cursor se puede ver que el segmento [AB] varía.
Ahora crearemos un lugar de objetos del punto A generado por las posiciones del cursor.
En la paleta de colores, active el color azul.
Para ello, utilice el icono ![]() de creación de un lugar de objetos generado por punto ligado.
de creación de un lugar de objetos generado por punto ligado.
Se le pide que haga clic en el objeto cuya traza generará el lugar : haga clic en el punto A.
Luego se le pide que haga clic sobre el punto ligado cuyas posiciones generarán el lugar : Haga clic sobre el punto del cursor (que estará parpadeando).
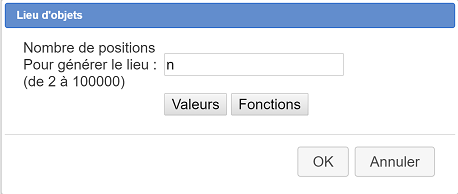
Se abre un cuadro de diálogo. Ingrese n en el campo Número de posiciones para generar el lugar de la siguiente manera :
De la misma manera crearemos el lugar de objeto del segmento generado por las posiciones del cursor.
Haga clic nuevamente en el icono ![]() , luego haga clic en el segmento [AB] y luego en el punto parpadeante del cursor.
, luego haga clic en el segmento [AB] y luego en el punto parpadeante del cursor.
En el cuadro de diálogo que se abre, ingrese n en el campo Número de posiciones para generar lugar y valide.
Utilizando el icono ![]() , oculte los puntos A y B y el segmento [AB] (haciendo clic sobre el segmento se le preguntará si desea designar el segmento o el lugar de objetos).
, oculte los puntos A y B y el segmento [AB] (haciendo clic sobre el segmento se le preguntará si desea designar el segmento o el lugar de objetos).
También puede ocultar todos los elementos del cursor y la recta vertical que pasa por O.
Guarde su figura con la herramienta ![]() de la barra de herramientas superior.
de la barra de herramientas superior.
Ahora, en la parte inferior derecha de la figura, haga clic en el botón = asociado a la variable n. En el campo Valor actual ingrese, por ejemplo, 399 y confirme.
Debajo está la figura obtenida.
Ahora puede hacer clic en los botones + y - para variar los valores de n y p como desee.