Toutes les versions de cet article : [English] [français]
Dans cet article je vais expliquer comment créer une fractale de Hilbert avec MathGraph32.
Il est conseillé pour cela d’utiliser la version JavaScript de MathGraph32 (version 6.4.5 ou ultérieure, avec les versions antérieures vous ne pourrez pas rouvrir la dernière figure une fois enregistrée).
L’idée de base est de partir de trois points libres A, B et C comme sur la figure ci-dessous.
A partir des points A, B et C, on a créé, dans cet ordre (l’ordre de création est important) :
Par exemple, le point D a été créé comme image de C par l’homothétie de centre A et rapport -1/4.
Les points suivants ont créés en utilisant des translations.
On a créé à la fin un polygone DEFGHKLMNOPQRSTU et une surface délimitée par ce polygone.
L’idée est de créer une macro-construction qui prenne comme objets sources les trois points A, B et C et comme objets finaux les points D, E, F, G, H, K, L, M, N, O,P, Q, R, S, T, U. Ces points seront cachés pour que la figure finale soit plus jolie.
Cette macro-construction étant un peu fastidieuse à créer, je vous propose de la télécharger dans le fichier ci-dessous.
Avec la figure ci-dessus, l’idée est de réappliquer la construction aux points D, E et F, puis aux points H, K et L, puis aux points N, O et P et enfin aux points R, S et T.
Nous obtenons alors la figure suivante (niveau de récursion de 1) :
Maintenant créez une nouvelle figure sans repère et sans longueur unité avec l’icône  .
.
Utilisez l’icône ![]() de la barre supérieure pour faire apparaître la barre d’outils supplémentaire.
de la barre supérieure pour faire apparaître la barre d’outils supplémentaire.
Cliquez sur l’icône  et choisissez Incorporer une construction depuis un fichier.
et choisissez Incorporer une construction depuis un fichier.
Allez chercher la construction Hilbert.mgc que vous avez téléchargée ci-dessus (après avoir dézippé le fichier) et validez.
Cette construction peut maintenant être utilisée dans votre nouvelle figure.
Créez deux points libres que nous nommerons A et B (icône  ).
).
Créez ensuite le segment [AB] (outil  ), la droite perpendiculaire à ce segment passant par B (outil
), la droite perpendiculaire à ce segment passant par B (outil  ), le cercle de centre B et passant par A (
), le cercle de centre B et passant par A ( ), l’intersection de ce cercle avec la perpendiculaire (
), l’intersection de ce cercle avec la perpendiculaire ( ).
).
Nommez C celui des deux points d’intersection qui est situé au-dessus du segment [AB].
Maintenant, avec l’outil  , masquez le segment, la perpendiculaire, le cercle et le point d’intersection autre que C.
, masquez le segment, la perpendiculaire, le cercle et le point d’intersection autre que C.
Déroulez la barre d’outil des affichages et cliquez sur l’icône ![]() de création d’une nouvelle macro.
de création d’une nouvelle macro.
Dans la liste déroulante, cliquez sur Macro de construction récursive
et validez.
Cliquez en haut et à gauche de la figure pour désigner l’endroit où sera affiché l’intitulé de la macro.
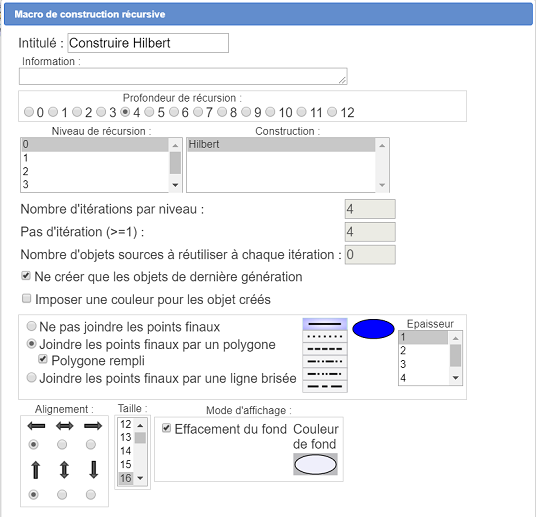
Une boîte de dialogue s’ouvre. Remplissez la comme ci-dessous puis validez.
N’oubliez pas, une fois la boîte de dialogue validée, de cliquer sur les points A, B et C qui sont les trois points sources utilisés pour la première itération de la construction.
L’intitulé de la macro apparait alors.
Il est préférable à ce niveau d’enregistrer votre figure.
Maintenant, activez dans la barre supérieure l’outil ![]() et cliquez sur l’intitulé de la macro pour l’exécuter.
et cliquez sur l’intitulé de la macro pour l’exécuter.
Vous obtenez la figure ci-dessous.
Remarquez que la figure reste dynamique : Vous pouvez capturer A et B.
A noter que la fluidité sera meilleure sous le navigateur Chrome qu’avec FireFox.
Quelques explications sur le paramétrage de la boîte de dialogue de création de la macro de construction récursive.
Comme nous l’avons vu plus haut, il faut bien à chaque itération réimplémenter quatre fois la construction Hilbert.
Quand nous avons implémenté la macro une première fois (CF figure en haut de la page) appliquée aux points D, E et F, il faut ensuite passer aux points H, K et L. Pour passer de D à H il faut sauter quatre des objets finaux créés par la macro construction Hilbert.
D’où la valeur 4 pour le pas d’itération.
On ne crée que les objets de dernière génération et on demande qu’ils soient joints par un polygone rempli d’une surface.
Attention : Si vous enregistrez votre figure après avoir exécuté la macro de construction récursive, le fichier généré sera très gros (plusieurs milliers d’objets).
Si votre machine est puissante, annulez l’exécution de la macro de construction récursive, utilisez l’outil  de modification d’objet graphique, cliquez sur la macro et passez la profondeur de récursion au niveau 5.
de modification d’objet graphique, cliquez sur la macro et passez la profondeur de récursion au niveau 5.
Vous pouvez télécharger la figure finale ci-dessous :
Ci-dessous la figure obtenue avec un niveau de récursion de 5.
Avec un tel niveau de récursion la construction de base est appliquée $4^5=1024$ fois !