Toutes les versions de cet article : [English] [Español] [français]
In this tutorial, vous will use a macro-construction and a macro of iterative construction to display a Barnsley fern.
You can refer to this Wikipedia article.
Start MathGraph32 (6.7.3 version or more recent) and use icon  to create a new figure with a frame. Choose an orthogonal frame without grid and without scale.
to create a new figure with a frame. Choose an orthogonal frame without grid and without scale.
Use icon  to create three real calculations named p1, p2 et p3 with the formulas underneath :
to create three real calculations named p1, p2 et p3 with the formulas underneath :
| Calculation name | Formula |
| p1 | 0.01 |
| p2 | 0.85 |
| p3 | 0.07 |
Creation of a p4 calculation is not necessary because the sum of the four probabilities is 1.
We will simulate a random experience by the choice of a random number laying between 0 and 1 (value 1 excluded).
Create the following real calculations :
| Calculation name | Formula | Explanation |
| alea | rand(0) | Random number of interval [0 ;1[ |
| case | if(alea<p1,1,if(alea<p1+p2,2,if(alea<p1+p2+p3,3,4))) | value of case is 1, 2, 3 ou 4 according to value of alea |
Now we are going to create eight matrices defined by their cells.
For this, expand the calculations toolbar and click on icon  to get more unusual tools available.
to get more unusual tools available.
In the list, choose Matrix.
For each matrix you must specify the number of rows and columns and then give a formula for each cell.
| Matrix name | Number of rows | Number of columns | Cell elements |
| A1 | 2 | 2 | $\begin{matrix}0 & 0\\ 0 & 0.16\end{matrix}$ |
| A2 | 2 | 2 | $\begin{matrix}0.85 & 0.04\\ -0.04 & 0.85\end{matrix}$ |
| A3 | 2 | 2 | $\begin{matrix}0.2 & -0.26\\ 0.23 & 0.22\end{matrix}$ |
| A4 | 2 | 2 | $\begin{matrix}-0.15 & 0.28\\ 0.26 & 0.24\end{matrix}$ |
| B1 | 2 | 1 | $\begin{matrix}0 \\ 0 \end{matrix}$ |
| B2 | 2 | 1 | $\begin{matrix}0 \\ 1.6 \end{matrix}$ |
| B3 | 2 | 1 | $\begin{matrix}0 \\ 1.6 \end{matrix}$ |
| B4 | 2 | 1 | $\begin{matrix}0 \\ 0.44 \end{matrix}$ |
Now let us define two matrices A (2 rows and 2 columns) and B (two rows and one column).
For this, expand again the calculations toolbar and click on icon  .
.
In the list choose item Matricial calculation.
Define A and B as shown underneath :
| Matrix name | Formula |
| A | if(case=1,A1,if(case=2,A2,if(case=3,A3,A4))) |
| B | if(case=1,B1,if(case=2,B2,if(case=3,B3,B4))) |
Expand again the calculations toolbar and click on icon  .
.
In the list, choose item Matrix.
Create matrix X as underneath (the two cells are null) :
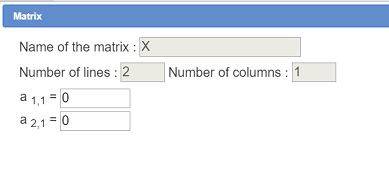
With tool  create a new real calculation named alea’ with this formula :
create a new real calculation named alea’ with this formula :
rand(0)+alea*0
We will explain later why this formula instead of rand(0).
Now create a new matricial calculation named Y with this formula :
A*X+B
All we have got to do now is create a point coordinates of which will be the elements of matrix Y.
In the color palette, activate the red color, expand the points toolbar annd click on icon (point creation via coordinates in a frame).
(point creation via coordinates in a frame).
Fill in the dialog box as above :
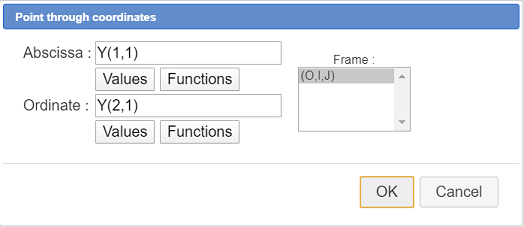
Now we are going to create a macro-construction with the following sources objects :
| Frame (0 ;I,J) |
| Calculation p1 |
| Calculation p2 |
| Calculation p3 |
| Calculation A1 |
| Matrix A2 |
| Matrix A3 |
| Matrix A4 |
| Matrix B1 |
| Matrix B2 |
| Matrix B3 |
| Matrix B4 |
| Calculation alea |
| Matrix X |
The final objects will be :
| Calculation alea’ |
| Matrix Y |
| The point of coordinates (Y(1,1), Y(2,1) |
For a construction to be valid, the final objects must depend of at least one source object. That is the reason why, in the formula of alea’ we used formula rand(0)+alea*0 so as alea’ will depend of source object alea.
Once this construction created, we will use a macro of iterative construction. This macro will, on each step, replace calculation alea by calculation alea’ and matrix X by matrix Y. The resulting cloud of points will represent our fern.
So tel us first create our macro-construction.
For this we must click on icon ![]() in the upper toolbar. This tool makes available more tools under the upper toolbar.
in the upper toolbar. This tool makes available more tools under the upper toolbar.
Then click on icon  and choose Numerical sources objects choice.
and choose Numerical sources objects choice.
A dialog box pops up.
To choose a numerical source object, you can eather select an element in the left list and then click on button Insert or double-click on an element in the left list.
You must get in the right list (dans cet ordre) :
| (0 ;I,J) |
| p1 |
| p2 |
| p3 |
| A1 |
| A2 |
| A3 |
| A4 |
| B1 |
| B2 |
| B3 |
| B4 |
| alea |
| X |
Beware : It is important that alea is added after matrices A1 to B4.
Validate your dialog box.
Our macro-construction has no graphical source object.
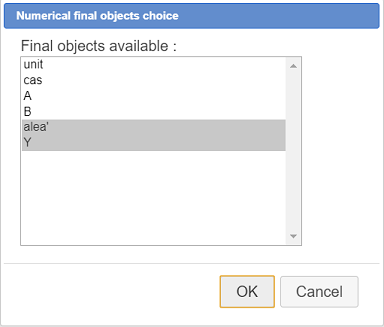
Let us now choose the final numerical objects.
Click on icon  then choose Numerical final objects choice.
then choose Numerical final objects choice.
In the left list, click on alea’ and Y to get them selected as shown above the validate.
Now we must set our only graphical final object which is the red point we created at the end (point defined via coordinates).
Click on icon  the choose Graphical final objects choice.
the choose Graphical final objects choice.
Click on the red point then click on button STOP on the bottom right side of the window.
Before finalizing our macro-construction, let us give to our red point the "pixel" style.
In the point style palette, choose the pixel style (bottom left). In the upper toolbar, click on palette tool  and then click on the red point to give it the selected style.
and then click on the red point to give it the selected style.
Now we are ready to finalize our construction.
Click on icon  the choose Finish current construction.
the choose Finish current construction.
A dialog box pops up.
In the field Construction name enter for instance Barnsley.
In the field Information, enter what follows :
#1:The frame
#2:Probability of case 1
#3:Probability of case 2
#4:Probability of case 3
#5:Matrix A for case 1
#6:Matrix A for case 2
#7:Matrix A for case 3
#8:Matrix A for case 4
#9:Matrix B for case 1
#10:Matrix A for case 2
#11:Matrix A for case 3
#12:Matrix A for case 4
#13:Calculation providing a random number betwwen 0 and 1
#14:Initial value of matrix XThe information edit content pupose is to give information to the user of the macro-construction.
Validate. Our construction is created..
If we would like to use this construction in another figure, we should first click on icon  then choose item Save a construction of the figure. Our construction would then be saved in a mgc file.
then choose item Save a construction of the figure. Our construction would then be saved in a mgc file.
Now we are going to use a macro of iterative construction which will use our macro-construction we just created.
For this, expand the dispaly toolbar and click on icon![]() displaying different macros types available .
displaying different macros types available .
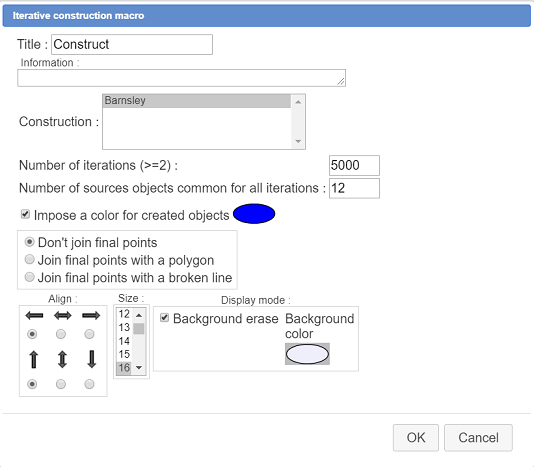
Since our figute contains a macro-construction, among the different macros availble is Iterative construction macro.
Click first on the spot the macro title is to be displayed at, on the top left corner of the figure.
A dialog box pops up.
Fill in this dialog box as shown here :
Once validated, another dialog box pops up allowing you to choose the sources objects. We must assignt to each of the 14 sources objects an compatible object of the figure.
In the example above, we are assigning calculation p3 to the fourth source object.
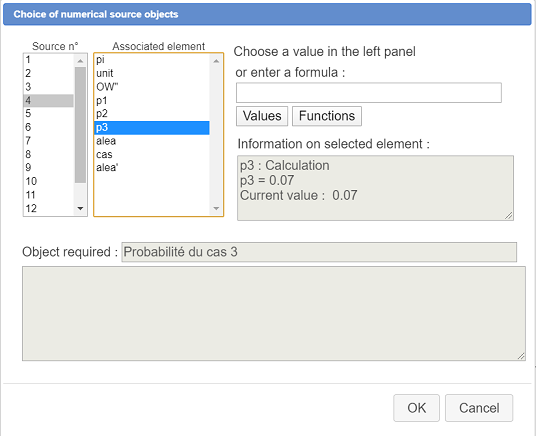
Here are the assignments to bo completed :
| Source element n° | Object to be assigned |
| 1 | (O ;i,j) |
| 2 | p1 |
| 3 | p2 |
| 4 | p3 |
| 5 | A1 |
| 6 | A2 |
| 7 | A3 |
| 8 | A4 |
| 9 | B1 |
| 10 | B2 |
| 11 | B3 |
| 12 | B4 |
| 13 | alea |
| 14 | X |
Then validate the dialog box.
Your macro macro Construct is now available in gthe top left corner of the figure.
To be noted : The 12 fisrt sources elements are the same for all the implements of the macro-construction.
For each new iteration these 12 objects are taken as sources objects, the thirteenth source object being the first final object of the former construction implementation (alea’) and the fourteenth being the second final object of the former implementation so matrix Y.
A this stage, it is a good idea to save your figure in a file because, once your macro Construct executed, the figure will contain a great number of objects and will generate a big file if you save it.
In the upper toolbar, you can now click on tool  (macro execution) then click on Construct.
(macro execution) then click on Construct.
After a few seconds (according to the power of your computer) you will see the Barnsley fern appear.
Here is the Base 64 code of the final figure followed by the figure displayed online.
Code Base 64 :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAABAAAABgAIQmFybnNsZXkBaiMxOlRoZSBmcmFtZQojMjpQcm9iYWJpbGl0eSBvZiBjYXNlIDEKIzM6UHJvYmFiaWxpdHkgb2YgY2FzZSAyCiM0OlByb2JhYmlsaXR5IG9mIGNhc2UgMwojNTpNYXRyaXggQSBmb3IgY2FzZSAxCiM2Ok1hdHJpeCBBIGZvciBjYXNlIDIKIzc6TWF0cml4IEEgZm9yIGNhc2UgMwojODpNYXRyaXggQSBmb3IgY2FzZSA0CiM5Ok1hdHJpeCBCIGZvciBjYXNlIDEKIzEwOk1hdHJpeCBBIGZvciBjYXNlIDIKIzExOk1hdHJpeCBBIGZvciBjYXNlIDMKIzEyOk1hdHJpeCBBIGZvciBjYXNlIDQKIzEzOkNhbGN1bGF0aW9uIHByb3ZpZGluZyBhIHJhbmRvbSBudW1iZXIgYmV0d3dlbiAwIGFuZCAxCiMxNDpJbml0aWFsIHZhbHVlIG9mIG1hdHJpeCBYAAAADgAAAAMCAAAAFP####8AAAABABFDRWxlbWVudEdlbmVyaXF1ZQAAAAAAGgAAABoAAAAAAAJwMf####8AAAABAAAAAAACcDL#####AAAAAQAAAAAAAnAz#####wAAAAEAAAAAAAJBMf####8AAAAfAAAAAAACQTL#####AAAAHwAAAAAAAkEz#####wAAAB8AAAAAAAJBNP####8AAAAfAAAAAAACQjH#####AAAAHwAAAAAAAkIy#####wAAAB8AAAAAAAJCM#####8AAAAfAAAAAAACQjT#####AAAAHwAAAAAABGFsZWH#####AAAAAQAAAAAAAVj#####AAAAH#####8AAAABAAdDQ2FsY3VsAP####8AA2NhcwA0c2koYWxlYTxwMSwxLHNpKGFsZWE8cDErcDIsMixzaShhbGVhPHAxK3AyK3AzLDMsNCkpKf####8AAAABAA1DRm9uY3Rpb24zVmFyAP####8AAAABAApDT3BlcmF0aW9uBP####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAAMAAAABAAAAAH#####AAAAAQAKQ0NvbnN0YW50ZT#wAAAAAAAAAAAAAgAAAAADBAAAAAQAAAAMAAAAAwAAAAAEAAAAAQAAAAQAAAACAAAABUAAAAAAAAAAAAAAAgAAAAADBAAAAAQAAAAMAAAAAwAAAAADAAAAAAQAAAABAAAABAAAAAIAAAAEAAAAAwAAAAVACAAAAAAAAAAAAAVAEAAAAAAAAP####8AAAABAAhDQ2FsY01hdAD#####AAFBAClzaShjYXM9MSxBMSxzaShjYXM9MixBMixzaShjYXM9MyxBMyxBNCkpKQAAAAIAAAAAAwgAAAAEAAAADgAAAAU#8AAAAAAAAAAAAAQAAAAEAAAAAgAAAAADCAAAAAQAAAAOAAAABUAAAAAAAAAAAAAABAAAAAUAAAACAAAAAAMIAAAABAAAAA4AAAAFQAgAAAAAAAAAAAAEAAAABgAAAAQAAAAHAAAABgD#####AAFCAClzaShjYXM9MSxCMSxzaShjYXM9MixCMixzaShjYXM9MyxCMyxCNCkpKQAAAAIAAAAAAwgAAAAEAAAADgAAAAU#8AAAAAAAAAAAAAQAAAAIAAAAAgAAAAADCAAAAAQAAAAOAAAABUAAAAAAAAAAAAAABAAAAAkAAAACAAAAAAMIAAAABAAAAA4AAAAFQAgAAAAAAAAAAAAEAAAACgAAAAQAAAALAAAAAQH#####AAVhbGVhJwAOcmFuZCgwKSthbGVhKjAAAAADAP####8AAAACAAlDRm9uY3Rpb24RAAAABQAAAAAAAAAAP+rYUPYavTYAAAADAgAAAAQAAAAMAAAABQAAAAAAAAAAAAAABgH#####AAFZAAVBKlgrQgAAAAMAAAAAAwIAAAAEAAAADwAAAAQAAAANAAAABAAAABD#####AAAAAQAQQ1BvaW50RGFuc1JlcGVyZQH#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABwAAAAAA#####wAAAAEACENUZXJtTWF0AAAAEgAAAAU#8AAAAAAAAAAAAAU#8AAAAAAAAAAAAAkAAAASAAAABUAAAAAAAAAAAAAABT#wAAAAAAAAAAAAAQAAACP#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0NgAAAAVACSH7VEQtGP####8AAAABAApDUG9pbnRCYXNlAP####8AAAAAAA4AAU8AwCgAAAAAAAAAAAAAAAAAAAAABQABQGFQAAAAAABAgGwo9cKPXP####8AAAABABRDRHJvaXRlRGlyZWN0aW9uRml4ZQD#####AQAAAAAQAAABAAAAAQAAAAEBP#AAAAAAAAD#####AAAAAQAPQ1BvaW50TGllRHJvaXRlAP####8AAAAAAA4AAUkAwBgAAAAAAAAAAAAAAAAAAAAABQABQEgAAAAAAAAAAAAC#####wAAAAEACUNEcm9pdGVBQgD#####AAAAAAAQAAABAAAAAQAAAAEAAAAD#####wAAAAEAFkNEcm9pdGVQZXJwZW5kaWN1bGFpcmUA#####wAAAAAAEAAAAQAAAAEAAAABAAAABP####8AAAABAAlDQ2VyY2xlT0EA#####wEAAAAAAAABAAAAAQAAAAP#####AAAAAQAQQ0ludERyb2l0ZUNlcmNsZQD#####AAAABQAAAAb#####AAAAAQAQQ1BvaW50TGllQmlwb2ludAD#####AQAAAAAQAAABAAAFAAEAAAAHAAAAEgD#####AAAAAAAOAAFKAMAoAAAAAAAAwBAAAAAAAAAAAAUAAgAAAAf#####AAAAAgAHQ1JlcGVyZQD#####AObm5gAAAAEAAAABAAAAAwAAAAkAAAAAAAAFAAAAAAAAAAAAAAAFAAAAAAAAAAAAAAAFP#AAAAAAAAAAAAAFP#AAAAAAAAD#####AAAAAQAKQ1VuaXRleFJlcAD#####AAR1bml0AAAACv####8AAAABAAtDSG9tb3RoZXRpZQD#####AAAAAQAAAAMDAAAABT#wAAAAAAAAAAAABAAAAAv#####AAAAAQALQ1BvaW50SW1hZ2UA#####wEAAAAAEAACVyIBAAABAAAAAAMAAAAM#####wAAAAEACUNMb25ndWV1cgD#####AAAAAQAAAA0AAAABAP####8AAnAxAAQwLjAxAAAABT+EeuFHrhR7AAAAAQD#####AAJwMgAEMC44NQAAAAU#6zMzMzMzMwAAAAEA#####wACcDMABDAuMDcAAAAFP7HrhR64UewAAAABAP####8ABGFsZWEAB3JhbmQoMCkAAAAHEQAAAAUAAAAAAAAAAD#pgoz0Pw88AAAAAQD#####AARjYXNlADRzaShhbGVhPHAxLDEsc2koYWxlYTxwMStwMiwyLHNpKGFsZWE8cDErcDIrcDMsMyw0KSkpAAAAAgAAAAADBAAAAAQAAAASAAAABAAAAA8AAAAFP#AAAAAAAAAAAAACAAAAAAMEAAAABAAAABIAAAADAAAAAAQAAAAPAAAABAAAABAAAAAFQAAAAAAAAAAAAAACAAAAAAMEAAAABAAAABIAAAADAAAAAAMAAAAABAAAAA8AAAAEAAAAEAAAAAQAAAARAAAABUAIAAAAAAAAAAAABUAQAAAAAAAA#####wAAAAEACENNYXRyaWNlAP####8AAkExAAAAAgAAAAIAAAAFAAAAAAAAAAAAAAAFAAAAAAAAAAAAAAAFAAAAAAAAAAAAAAAFP8R64UeuFHsAAAAYAP####8AAkEyAAAAAgAAAAIAAAAFP+szMzMzMzMAAAAFP6R64UeuFHv#####AAAAAQAMQ01vaW5zVW5haXJlAAAABT+keuFHrhR7AAAABT#rMzMzMzMzAAAAGAD#####AAJBMwAAAAIAAAACAAAABT#JmZmZmZmaAAAAGQAAAAU#0KPXCj1wpAAAAAU#zXCj1wo9cQAAAAU#zCj1wo9cKQAAABgA#####wACQTQAAAACAAAAAgAAABkAAAAFP8MzMzMzMzMAAAAFP9HrhR64UewAAAAFP9Cj1wo9cKQAAAAFP864UeuFHrgAAAAYAP####8AAkIxAAAAAgAAAAEAAAAFAAAAAAAAAAAAAAAFAAAAAAAAAAAAAAAYAP####8AAkIyAAAAAgAAAAEAAAAFAAAAAAAAAAAAAAAFP#mZmZmZmZoAAAAYAP####8AAkIzAAAAAgAAAAEAAAAFAAAAAAAAAAAAAAAFP#mZmZmZmZoAAAAYAP####8AAkI0AAAAAgAAAAEAAAAFAAAAAAAAAAAAAAAFP9wo9cKPXCkAAAAGAP####8AAUEALHNpKGNhc2U9MSxBMSxzaShjYXNlPTIsQTIsc2koY2FzZT0zLEEzLEE0KSkpAAAAAgAAAAADCAAAAAQAAAATAAAABT#wAAAAAAAAAAAABAAAABQAAAACAAAAAAMIAAAABAAAABMAAAAFQAAAAAAAAAAAAAAEAAAAFQAAAAIAAAAAAwgAAAAEAAAAEwAAAAVACAAAAAAAAAAAAAQAAAAWAAAABAAAABcAAAAGAP####8AAUIALHNpKGNhc2U9MSxCMSxzaShjYXNlPTIsQjIsc2koY2FzZT0zLEIzLEI0KSkpAAAAAgAAAAADCAAAAAQAAAATAAAABT#wAAAAAAAAAAAABAAAABgAAAACAAAAAAMIAAAABAAAABMAAAAFQAAAAAAAAAAAAAAEAAAAGQAAAAIAAAAAAwgAAAAEAAAAEwAAAAVACAAAAAAAAAAAAAQAAAAaAAAABAAAABsAAAAYAP####8AAVgAAAACAAAAAQAAAAUAAAAAAAAAAAAAAAUAAAAAAAAAAAAAAAEA#####wAFYWxlYScADnJhbmQoMCkrYWxlYSowAAAAAwAAAAAHEQAAAAUAAAAAAAAAAD#q2FD2Gr02AAAAAwIAAAAEAAAAEgAAAAUAAAAAAAAAAAAAAAYA#####wABWQAFQSpYK0IAAAADAAAAAAMCAAAABAAAABwAAAAEAAAAHgAAAAQAAAAdAAAACAD#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABwAAAAAKAAAACQAAACAAAAAFP#AAAAAAAAAAAAAFP#AAAAAAAAAAAAAJAAAAIAAAAAVAAAAAAAAAAAAAAAU#8AAAAAAAAP####8AAAABABtDTWFjcm9Db25zdHJ1Y3Rpb25JdGVyYXRpdmUA#####wAAAP8BAAD#####EEAxgAAAAAAAQDOFHrhR64YCAe#v+wAAAAAAAAAAAAAABQAAAAAAAAAAAAlDb25zdHJ1Y3QAAAAAAA4AAAAKAAAADwAAABAAAAARAAAAFAAAABUAAAAWAAAAFwAAABgAAAAZAAAAGgAAABsAAAASAAAAHgAAAAAAABOIAAAADAEAAP8AAAAAAAAADv##########Voici la figure obtenue :