Toutes les versions de cet article : [English] [Español] [français]
Este ejemplo requiere mucha potencia informática, pero el motor de cálculo de MathGraph32 es lo suficientemente potente para ello.
Puedes ver la figura en acción a continuación. Haz clic en la macro Animar la rueda para iniciar la animación.
Inicia MathGraph32 (versión JavaScript) y usa el icono  para crear una figura con un referencial ortonormal.
para crear una figura con un referencial ortonormal.
Usa el ícono  (opciones de figura) y verifica que la casilla de radianes esté marcada para la unidad de ángulo.
(opciones de figura) y verifica que la casilla de radianes esté marcada para la unidad de ángulo.
Al desplegar la barra de herramientas de cálculos (tercera barra de herramientas desde abajo), usa el ícono  y crea una función f como se muestra a continuación. Deja marcada la casilla Trazar curva.
y crea una función f como se muestra a continuación. Deja marcada la casilla Trazar curva.
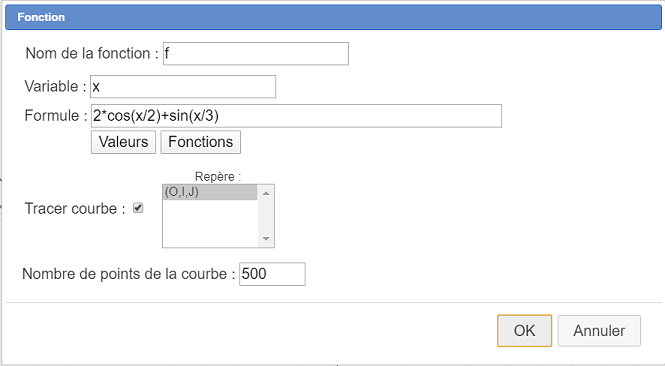
Ahora le pediremos a MathGraph32 que calcule la derivada formal de la función f.
Para ello, utiliza el icono  . En el cuadro de diálogo que se abre, la función f ya está seleccionada. Nombra esta derivada f ’ y valida.
. En el cuadro de diálogo que se abre, la función f ya está seleccionada. Nombra esta derivada f ’ y valida.
Un pequeño recordatorio preliminar : la longitud (algebraica) del arco de curva de f entre la abscisa 0 y a viene dada por la fórmula $ \int_{0}^{a} \sqrt{1+( f’ (x))^2}dx $ (con f diferenciable con derivada continua).
Usa el ícono  para crear una función g como se muestra a continuación, desmarca la casilla Trazar curva (esta función se usará para calcular longitudes aproximadas de arcos de curva).
para crear una función g como se muestra a continuación, desmarca la casilla Trazar curva (esta función se usará para calcular longitudes aproximadas de arcos de curva).
Esta es la fórmula para ingresar g(x) : integrale(sqrt(1+f'(t)^2),t,0,x)
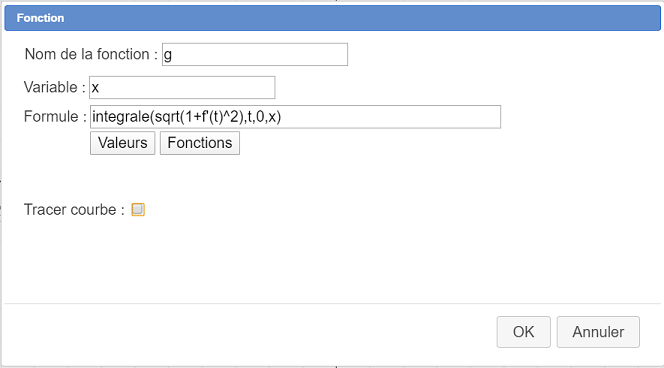
Ten en cuenta que al hacer clic en el botón Funciones se te ofrece una lista de funciones predefinidas con su sintaxis. Aquí el primer parámetro de la función integral predefinida es la fórmula a integrar, el segundo la variable formal utilizada para la función a integrar (aquí t), el tercero es el límite inferior de integración y el último el límite superior de integración.
g(x) representará por tanto la longitud algebraica del arco de curva de f entre las abscisas 0 y x.
Ahora usa el ícono  para crear dos cálculos reales como se explica a continuación :
para crear dos cálculos reales como se explica a continuación :
| Nombre del cálculo | Fórmula | Explicaciones |
| L | g(16) | L representará la longitud algebraica del arco de curva de f entre las abscisas 0 y 16. Es positivo. |
| L’ | g(-16) | L’ representará la longitud algebraica del arco de curva de f entre las abscisas 0 y -16. Es negativo. |
Ahora vamos a crear un cursor cuyos valores irán de L’ a L.
Para ello, activa el icono  en la barra de herramientas de cálculo ; haz clic en la parte superior izquierda de la figura.
en la barra de herramientas de cálculo ; haz clic en la parte superior izquierda de la figura.
Rellena el cuadro de diálogo de la siguiente manera :
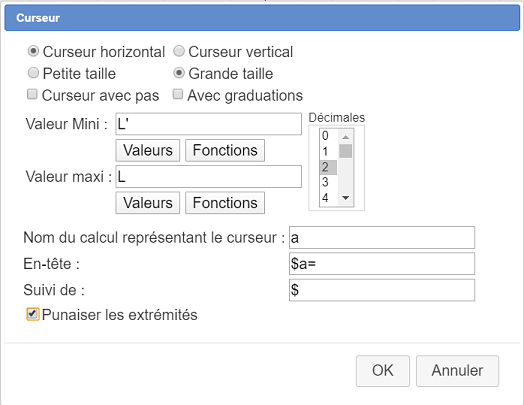
Aquí pedimos un cursor grande con valores no enteros. Los $ son para que el encabezado se muestre en modo LaTeX.
El valor de a representará el valor algebraico de la longitud recorrida por la rueda.
Para cada valor de a necesitamos conocer la abscisa x de la curva por la cual se ha recorrido esta longitud.
Calcularemos x como el valor aproximado de una solución de ecuación.
Para ello, utiliza el icono  y rellena el cuadro de diálogo como se muestra a continuación :
y rellena el cuadro de diálogo como se muestra a continuación :
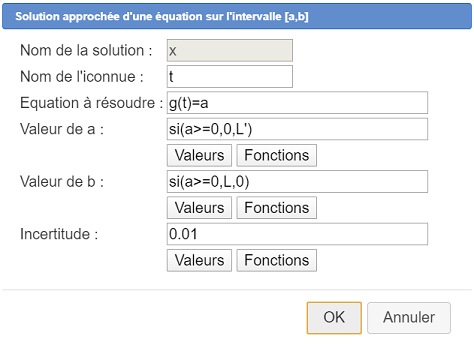
La ecuación a resolver es g(t)=a (de incógnita t) y pedimos la solución de esta ecuación en el intervalo [0 ; L] si a es positivo y [L’ ; 0] si a es negativo (cuanto menor sea el intervalo de búsqueda, más rápidos serán los cálculos). Para ello usa un si en las fórmulas de los límites inferior y superior del intervalo de búsqueda.
El cálculo de x es voraz en potencia de cálculo porque cada cálculo de x se realiza por dicotomía para aproximar la solución y, además, la función g utilizada usa un cálculo aproximado de la integral.
Ahora es el momento de crear la "rueda" que girará sobre la curva.
Primero creemos una variable r que representará el radio de esta rueda.
Utiliza el icono  para crear una variable llamada r con un valor mínimo de 0,25, un valor máximo de 1,5, un paso de incremento de 0,25 y un valor actual de 1. Marca la casilla diálogo asociado. Un elemento gráfico en la parte inferior derecha de la figura te permitirá variar r haciendo clic en los botones + y -.
para crear una variable llamada r con un valor mínimo de 0,25, un valor máximo de 1,5, un paso de incremento de 0,25 y un valor actual de 1. Marca la casilla diálogo asociado. Un elemento gráfico en la parte inferior derecha de la figura te permitirá variar r haciendo clic en los botones + y -.
En la paleta de colores, activa el color marrón.
Utiliza el icono  y solicita el punto de coordenadas (x ; 0).
y solicita el punto de coordenadas (x ; 0).
Desplegando la barra de visualizaciones, usa el icono  para crear una visualización LaTeX vinculada al último punto creado con el código LaTeX y solicita una visualización centrada horizontalmente y debajo del punto. Luego puedes capturar esta visualización con la herramienta
para crear una visualización LaTeX vinculada al último punto creado con el código LaTeX y solicita una visualización centrada horizontalmente y debajo del punto. Luego puedes capturar esta visualización con la herramienta  para bajarla ligeramente. La creación de esta visualización LaTeX no es esencial para lo que sigue.
para bajarla ligeramente. La creación de esta visualización LaTeX no es esencial para lo que sigue.
Nuevamente usa el ícono  y solicita el punto de coordenadas (x ; f(x)) que es por lo tanto el punto de la curva de abscisa x.
y solicita el punto de coordenadas (x ; f(x)) que es por lo tanto el punto de la curva de abscisa x.
Activa el estilo de línea punteada y utiliza el icono  para unir los puntos de coordenadas (x ; 0) y (x ; f(x)) con un segmento).
para unir los puntos de coordenadas (x ; 0) y (x ; f(x)) con un segmento).
Ahora trazaremos la tangente a la curva en este último punto.
Para ello, utiliza el icono  , haz clic en el último punto creado y, en el cuadro de diálogo que se abre, introduce como coeficiente director : f’(x).
, haz clic en el último punto creado y, en el cuadro de diálogo que se abre, introduce como coeficiente director : f’(x).
Ahora usa la herramienta  para crear la perpendicular a esta tangente que pasa por el punto de la curva : primero haz clic en la tangente y luego en el punto de coordenadas (x ;f (x)). Esta perpendicular es la normal a la curva en este punto.
para crear la perpendicular a esta tangente que pasa por el punto de la curva : primero haz clic en la tangente y luego en el punto de coordenadas (x ;f (x)). Esta perpendicular es la normal a la curva en este punto.
Usa el ícono  para crear la circunferencia de centro en el punto de coordenadas (x ; f(x)) y radio r (donde r es la variable definida anteriormente).
para crear la circunferencia de centro en el punto de coordenadas (x ; f(x)) y radio r (donde r es la variable definida anteriormente).
Usa la herramienta  para crear la intersección de esta circunferencia con la normal a la curva (simplemente haz clic en la intersección cuando se muestre esta intersección cerca del puntero del mouse).
para crear la intersección de esta circunferencia con la normal a la curva (simplemente haz clic en la intersección cuando se muestre esta intersección cerca del puntero del mouse).
Aparecen dos puntos de intersección. Solo usaremos el que se encuentra situado arriba de la tangente. Lo llamaremos A.
Vamos a crear la rueda. En la paleta de colores, activa el color azul y elige un estilo de línea continua de dos píxeles de grosor.
Usa la herramienta  para crear la circunferencia con centro A y que por el punto de la curva. Esta circunferencia será nuestra "rueda".
para crear la circunferencia con centro A y que por el punto de la curva. Esta circunferencia será nuestra "rueda".
Ahora usa la herramienta  de la barra de herramientas superior para ocultar : la primera circunferencia, el segundo punto de intersección y las dos rectas (tangente y normal).
de la barra de herramientas superior para ocultar : la primera circunferencia, el segundo punto de intersección y las dos rectas (tangente y normal).
Ahora crearemos radios para esta rueda.
En la paleta de colores activa el color rojo y activa el estilo de línea punteada.
Despliega la barra de herramientas de transformaciones y usa el icono  (rotación)
(rotación)
Primero haz clic en el centro de la última circunferencia (centro de la rueda). Un cuadro de diálogo te pregunta por el ángulo de rotación. Como ángulo de rotación, ingresa -a/r y luego valida de la siguiente manera :
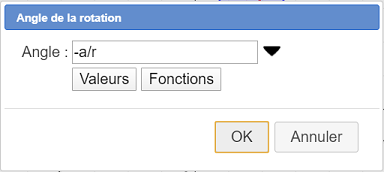
Usamos aquí la fórmula que da la longitud de un arco de circunferencia : $Long = r \times \vartheta$ donde aquí la longitud del arco es a. Pero no olvides el signo -.
Luego haz clic en el punto de la curva de coordenadas (x ; f(x)).
El punto imagen que aparece representa la posición actual del punto de la rueda que estaba en la parte inferior de la rueda cuando la rueda estaba en el punto de abscisa 0.
Vuelve a utilizar el icono de rotación  y haz clic en el centro de la rueda. Esta vez elige como ángulo pi/3 (puedes hacer clic en la flecha negra para desplegar una lista de ángulos predefinidos como se muestra a continuación).
y haz clic en el centro de la rueda. Esta vez elige como ángulo pi/3 (puedes hacer clic en la flecha negra para desplegar una lista de ángulos predefinidos como se muestra a continuación).
Haz clic en el punto creado anteriormente. Haz clic nuevamente en el último punto y así sucesivamente 5 veces para tener 6 puntos espaciados uniformemente en la rueda.
Luego une estos puntos de dos en dos opuestos por segmentos para tener los "radios" de la rueda así :
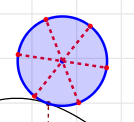
.
Ya puedes ver que capturando el punto móvil del cursor hacia arriba y hacia la izquierda la rueda gira sin deslizar sobre la curva.
Ahora vamos a crear una macro que automáticamente haga girar la rueda.
Para hacer esto, despliega la barra de herramientas de visualización y haz clic a su derecha en el icono  como se muestra a continuación, luego elige de la lista Macro de animación de un punto ligado.
como se muestra a continuación, luego elige de la lista Macro de animación de un punto ligado.

Primero se te pide que hagas clic en el lugar donde se mostrará la macro : haz clic debajo del cursor.
Rellena el cuadro de diálogo que aparece a continuación :
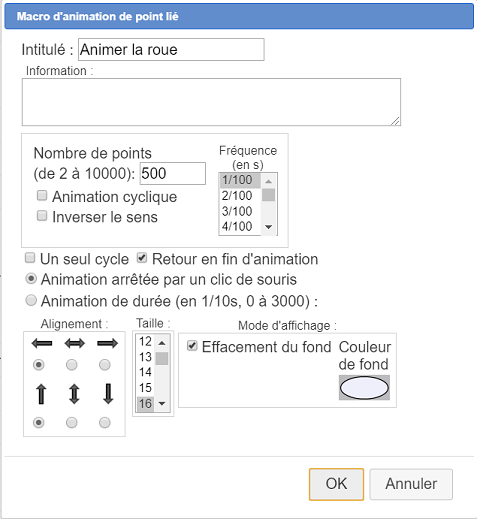
Ahora para lanzar la animación, todo lo que tienes que hacer es activar la herramienta  en la barra de herramientas superior y hacer clic en el título de la macro. Vuelve a hacer clic en la figura para detener la animación.
en la barra de herramientas superior y hacer clic en el título de la macro. Vuelve a hacer clic en la figura para detener la animación.
En la parte inferior derecha de la figura, puedes hacer clic en los botones + y - para variar el radio de la rueda.
Aportemos una mejora final a esta figura agregando un editor de fórmulas que te permitirá modificar la fórmula de f(x) directamente en la figura.
Expande la barra de herramientas de visualización y haz clic en el icono  .
.
Luego haz clic donde se mostrará este editor (por ejemplo, en la parte superior y al centro de la figura) y completa el cuadro de diálogo como se muestra a continuación y valida :
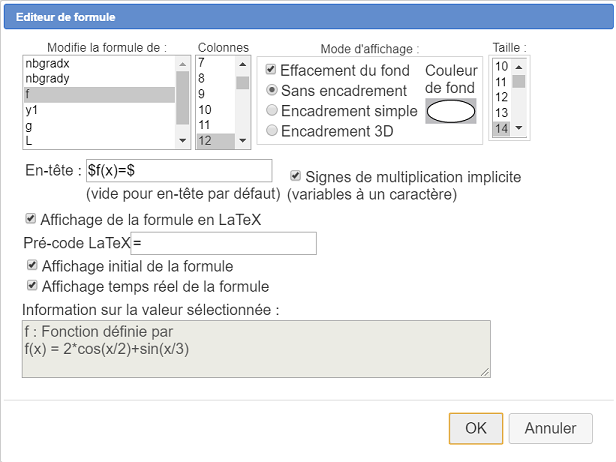
Ahora puedes cambiar la fórmula de la función f. ¡Es mejor que la función sea continua y no demasiado irregular !
A continuación se muestra el código Base 64 para esta figura :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAATeAAACygAAAQEAAAAAAAAAAAAAAGb#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAPQ1ZhcmlhYmxlQm9ybmVlAP####8AAXI#8AAAAAAAAD#QAAAAAAAAP#QAAAAAAAA#0AAAAAAAAAEABDAuMjUABDEuMjUABDAuMjX#####AAAAAQAKQ1BvaW50QmFzZQD#####AAAAAAAOAAFPAMAoAAAAAAAAAAAAAAAAAAAAAAUAAUB9QAAAAAAAQHINcKPXCj7#####AAAAAQAUQ0Ryb2l0ZURpcmVjdGlvbkZpeGUA#####wEAAAAAEAAAAQAAAAEAAAACAT#wAAAAAAAA#####wAAAAEAD0NQb2ludExpZURyb2l0ZQD#####AAAAAAEOAAFJAMAYAAAAAAAAAAAAAAAAAAAAAAUAAUA6AAAAAAAAAAAAA#####8AAAABAAlDRHJvaXRlQUIA#####wAAAAAAEAAAAQAAAAEAAAACAAAABP####8AAAABABZDRHJvaXRlUGVycGVuZGljdWxhaXJlAP####8AAAAAABAAAAEAAAABAAAAAgAAAAX#####AAAAAQAJQ0NlcmNsZU9BAP####8BAAAAAAAAAQAAAAIAAAAE#####wAAAAEAEENJbnREcm9pdGVDZXJjbGUA#####wAAAAYAAAAH#####wAAAAEAEENQb2ludExpZUJpcG9pbnQA#####wEAAAAAEAAAAQAABQABAAAACAAAAAoA#####wAAAAABDgABSgDAKAAAAAAAAMAQAAAAAAAAAAAFAAIAAAAI#####wAAAAIAB0NSZXBlcmUA#####wDm5uYAAAABAAAAAgAAAAQAAAAKAQEAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAA#####wAAAAEACkNVbml0ZXhSZXAA#####wAEdW5pdAAAAAv#####AAAAAQALQ0hvbW90aGV0aWUA#####wAAAAL#####AAAAAQAKQ09wZXJhdGlvbgMAAAABP#AAAAAAAAD#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAADP####8AAAABAAtDUG9pbnRJbWFnZQD#####AQAAAAAQAAJXIgEAAAEAAAAABAAAAA3#####AAAAAQAJQ0xvbmd1ZXVyAP####8AAAACAAAADv####8AAAABAAdDQ2FsY3VsAP####8AB25iZ3JhZHgAAjIwAAAAAUA0AAAAAAAAAAAAEgD#####AAduYmdyYWR5AAIyMAAAAAFANAAAAAAAAP####8AAAABABRDSW1wbGVtZW50YXRpb25Qcm90bwD#####ABRHcmFkdWF0aW9uQXhlc1JlcGVyZQAAABsAAAAIAAAAAwAAAAsAAAAQAAAAEf####8AAAABABNDQWJzY2lzc2VPcmlnaW5lUmVwAAAAABIABWFic29yAAAAC#####8AAAABABNDT3Jkb25uZWVPcmlnaW5lUmVwAAAAABIABW9yZG9yAAAACwAAAAwAAAAAEgAGdW5pdGV4AAAAC#####8AAAABAApDVW5pdGV5UmVwAAAAABIABnVuaXRleQAAAAv#####AAAAAQAQQ1BvaW50RGFuc1JlcGVyZQAAAAASAAAAAAAQAAABAAAFAAAAAAsAAAAPAAAAEwAAAA8AAAAUAAAAFwAAAAASAAAAAAAQAAABAAAFAAAAAAsAAAAOAAAAAA8AAAATAAAADwAAABUAAAAPAAAAFAAAABcAAAAAEgAAAAAAEAAAAQAABQAAAAALAAAADwAAABMAAAAOAAAAAA8AAAAUAAAADwAAABYAAAANAAAAABIAAAAXAAAADwAAABAAAAAQAAAAABIAAAAAABAAAAEAAAUAAAAAGAAAABoAAAANAAAAABIAAAAXAAAADwAAABEAAAAQAAAAABIAAAAAABAAAAEAAAUAAAAAGQAAABz#####AAAAAQAIQ1NlZ21lbnQAAAAAEgEAAAAAEAAAAQAAAAEAAAAYAAAAGwAAABgAAAAAEgEAAAAAEAAAAQAAAAEAAAAZAAAAHQAAAAUAAAAAEgEAAAAACwABVwDAFAAAAAAAAMA0AAAAAAAAAAAFAAE#3FZ4mrzfDgAAAB7#####AAAAAgAIQ01lc3VyZVgAAAAAEgAGeENvb3JkAAAACwAAACAAAAASAAAAABIABWFic3cxAAZ4Q29vcmQAAAAPAAAAIf####8AAAACABJDTGlldU9iamV0UGFyUHRMaWUBAAAAEgBmZmYAAAAAACAAAAAPAAAAEAAAACAAAAACAAAAIAAAACAAAAASAAAAABIABWFic3cyAA0yKmFic29yLWFic3cxAAAADgEAAAAOAgAAAAFAAAAAAAAAAAAAAA8AAAATAAAADwAAACIAAAAXAAAAABIBAAAAABAAAAEAAAUAAAAACwAAAA8AAAAkAAAADwAAABQAAAAaAQAAABIAZmZmAAAAAAAlAAAADwAAABAAAAAgAAAABQAAACAAAAAhAAAAIgAAACQAAAAlAAAABQAAAAASAQAAAAALAAFSAEAgAAAAAAAAwCAAAAAAAAAAAAUAAT#RG06BtOgfAAAAH#####8AAAACAAhDTWVzdXJlWQAAAAASAAZ5Q29vcmQAAAALAAAAJwAAABIAAAAAEgAFb3JkcjEABnlDb29yZAAAAA8AAAAoAAAAGgEAAAASAGZmZgAAAAAAJwAAAA8AAAARAAAAJwAAAAIAAAAnAAAAJwAAABIAAAAAEgAFb3JkcjIADTIqb3Jkb3Itb3JkcjEAAAAOAQAAAA4CAAAAAUAAAAAAAAAAAAAADwAAABQAAAAPAAAAKQAAABcAAAAAEgEAAAAAEAAAAQAABQAAAAALAAAADwAAABMAAAAPAAAAKwAAABoBAAAAEgBmZmYAAAAAACwAAAAPAAAAEQAAACcAAAAFAAAAJwAAACgAAAApAAAAKwAAACz#####AAAAAgAMQ0NvbW1lbnRhaXJlAAAAABIBZmZmAAAAAAAAAAAAQBgAAAAAAAAAAAAAACALAAH###8AAAABAAAAAAAAAAEAAAAAAAAAAAALI1ZhbChhYnN3MSkAAAAaAQAAABIAZmZmAAAAAAAuAAAADwAAABAAAAAgAAAABAAAACAAAAAhAAAAIgAAAC4AAAAcAAAAABIBZmZmAAAAAAAAAAAAQBgAAAAAAAAAAAAAACULAAH###8AAAABAAAAAAAAAAEAAAAAAAAAAAALI1ZhbChhYnN3MikAAAAaAQAAABIAZmZmAAAAAAAwAAAADwAAABAAAAAgAAAABgAAACAAAAAhAAAAIgAAACQAAAAlAAAAMAAAABwAAAAAEgFmZmYAwCAAAAAAAAA#8AAAAAAAAAAAAAAAJwsAAf###wAAAAIAAAABAAAAAQAAAAAAAAAAAAsjVmFsKG9yZHIxKQAAABoBAAAAEgBmZmYAAAAAADIAAAAPAAAAEQAAACcAAAAEAAAAJwAAACgAAAApAAAAMgAAABwAAAAAEgFmZmYAwBwAAAAAAAAAAAAAAAAAAAAAAAAALAsAAf###wAAAAIAAAABAAAAAQAAAAAAAAAAAAsjVmFsKG9yZHIyKQAAABoBAAAAEgBmZmYAAAAAADQAAAAPAAAAEQAAACcAAAAGAAAAJwAAACgAAAApAAAAKwAAACwAAAA0#####wAAAAEABUNGb25jAP####8AAWYAEzIqY29zKHgvMikrc2luKHgvMykAAAAOAAAAAA4CAAAAAUAAAAAAAAAA#####wAAAAIACUNGb25jdGlvbgQAAAAOA#####8AAAACABFDVmFyaWFibGVGb3JtZWxsZQAAAAAAAAABQAAAAAAAAAAAAAAeAwAAAA4DAAAAHwAAAAAAAAABQAgAAAAAAAAAAXgAAAAFAP####8BAAAAABAAAXgAAAAAAAAAAABACAAAAAAAAAAABQABv#5GMaUabogAAAAFAAAAGQD#####AAJ4MQAAAAsAAAA3AAAAEgD#####AAJ5MQAFZih4MSn#####AAAAAQAOQ0FwcGVsRm9uY3Rpb24AAAA2AAAADwAAADgAAAAXAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAsAAAAPAAAAOAAAAA8AAAA5#####wAAAAIADUNMaWV1RGVQb2ludHMA#####wAAAAAAAAABAAAAOgAAAfQAAQAAADcAAAAEAAAANwAAADgAAAA5AAAAOv####8AAAABAAhDRGVyaXZlZQD#####AAJmJwAAADYAAAAdAP####8AAWcAIGludGVncmFsZShzcXJ0KDErZicodCleMiksdCwwLHgp#####wAAAAEAFUNJbnRlZ3JhbGVEYW5zRm9ybXVsZQABdAAAAB4BAAAADgAAAAABP#AAAAAAAAD#####AAAAAQAKQ1B1aXNzYW5jZQAAACAAAAA8AAAAHwAAAAEAAAABQAAAAAAAAAAAAAABAAAAAAAAAAAAAAAfAAAAAAABeAAAABIA#####wABTAAFZygxNikAAAAgAAAAPQAAAAFAMAAAAAAAAAAAABIA#####wACTCcABmcoLTE2KQAAACAAAAA9#####wAAAAEADENNb2luc1VuYWlyZQAAAAFAMAAAAAAAAAAAAAMA#####wAAAAAAEAAAAEAIAAAAAAAAAAAAAAAAAAAAAAUAAEBFgAAAAAAAQD#XCj1wo9gAAAATAP####8AB0N1cnNldXIAAAAFAAAABQAAAAMAAAA#AAAAPgAAAEAAAAAEAAAAAEEBAAAAABAAAAEAAAABAAAAQAE#8AAAAAAAAAAAAAUBAAAAQQAAAAAAEAAAAMAIAAAAAAAAP#AAAAAAAAAAAAUAAEBtQAAAAAAAAAAAQgAAAA0AAAAAQQAAAEAAAAAOAwAAAA8AAAA#AAAADgEAAAAPAAAAPwAAAA8AAAA+AAAAEAAAAABBAQAAAAANAAJPMQDAEAAAAAAAAEAQAAAAAAAAAAAFAAAAAEMAAABEAAAADQAAAABBAAAAQAAAAA4DAAAADgEAAAABP#AAAAAAAAAAAAAPAAAAPwAAAA4BAAAADwAAAD4AAAAPAAAAPwAAABAAAAAAQQEAAAAADQACSTEAwAAAAAAAAABACAAAAAAAAAAABQAAAABDAAAARgAAABgBAAAAQQAAAAAAEAAAAQAAAAEAAABAAAAAQwAAAAUBAAAAQQAAAAABEAACazEAwAAAAAAAAABAAAAAAAAAAAAAAQABP+JTJTJTJTIAAABI#####wAAAAIAD0NNZXN1cmVBYnNjaXNzZQEAAABBAAFhAAAARQAAAEcAAABJ#####wAAAAEAD0NWYWxldXJBZmZpY2hlZQEAAABBAAAAAAAAAAAAAAAAAMAYAAAAAAAAAAAAAABJDwAB####AAAAAQAAAAIAAAABAAAAAAAAAAAAAyRhPQABJAIAAABK#####wAAAAIAEUNTb2x1dGlvbkVxdWF0aW9uAP####8AAXgAAXQAAAAOCAAAACAAAAA9AAAAHwAAAAAAAAAPAAAASgAAAA4BAAAAIAAAAD0AAAAfAAAAAAAAAA8AAABK#####wAAAAEADUNGb25jdGlvbjNWYXIAAAAADgcAAAAPAAAASgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAA8AAAA#AAAAKQAAAAAOBwAAAA8AAABKAAAAAQAAAAAAAAAAAAAADwAAAD4AAAABAAAAAAAAAAAAAAABP4R64UeuFHsAAAAXAP####8AfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAsAAAAPAAAATAAAAAEAAAAAAAAAAP####8AAAACAAZDTGF0ZXgA#####wB#AAAAv#AAAAAAAABAGAAAAAAAAAAAAAAATRIAAAAAAAEAAAAAAAAAAQAAAAAAAAAAAAF4AAAAFwD#####AH8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAALAAAADwAAAEwAAAAgAAAANgAAAA8AAABMAAAAGAD#####AH8AAAAQAAABAAABAQAAAE0AAABP#####wAAAAEACUNEcm9pdGVPbQD#####AQAA#wAQAAABAAABAQAAAAsAAABPAAAAIAAAADwAAAAPAAAATAAAAAcA#####wEAAP8AEAAAAQAAAQEAAABPAAAAUf####8AAAACAAlDQ2VyY2xlT1IA#####wEAAP8AAAEBAAAATwAAAA8AAAABAAAAAAkA#####wAAAFIAAABTAAAACgD#####AQAA#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABAAAAVAAAAAoA#####wAAAP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAgAAAFQAAAAIAP####8AAAD#AAAAAgAAAFYAAABP#####wAAAAEACUNSb3RhdGlvbgD#####AAAAVgAAACUAAAAOAwAAAA8AAABKAAAADwAAAAEAAAAQAP####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAE8AAABYAAAALQD#####AAAAVgAAAA4DAAAADwAAAAAAAAABQAgAAAAAAAAAAAAQAP####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFkAAABaAAAAEAD#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABbAAAAWgAAABAA#####wD#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAXAAAAFoAAAAQAP####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAF0AAABaAAAAEAD#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABeAAAAWgAAABgA#####wD#AAAAEAAAAQAAAQIAAABZAAAAXQAAABgA#####wD#AAAAEAAAAQAAAQIAAABbAAAAXgAAABgA#####wD#AAAAEAAAAQAAAQIAAABcAAAAX#####8AAAABAA5DU3VyZmFjZURpc3F1ZQD#####AAAA#wAAAAAABQAAAFf#####AAAAAgAXQ01hY3JvQW5pbWF0aW9uUG9pbnRMaWUA#####wAAAP8BAAD#####EEBFgAAAAAAAQFL1wo9cKPYCAe#v+wAAAAAAAAAAAAAAAQAAAAAAAAAAAA5BbmltZXIgbGEgcm91ZQAAAAAAAAoAAAH0AAAAAAAAAEkAAQD#####AAAABAAPQ0VkaXRldXJGb3JtdWxlAP####8AAAAAAQAA#####w5AdpAAAAAAAEA11wo9cKPYAAH###8AAAACAAAAAAAAAAEAAAAAAAAAAAAAADYAByRmKHgpPSQAAAAMAQEAAT0BAQAAAA###########w==