Calculus and representation of complex numbers with MathGraph32

This article has been adapted to the JavaScript version of MathGraph32.

MathGraph32 allows calculation and graphical representation of complex numers.

It is possible to create owner defined complex function of one (up to six) variables, to create a point in a frame defined through an affix, to measure teh affix of a point in a frame, to create recurrent complex sequences type of u(n+1) = f[u(n)] and to represent these sequences in a frame.

A complex calculation may use every complex or real number defined before.

A real calculation can only use real calculations or measures defined before.

If you want to use the real part, imaginary part, modulus or argument of a complex number in a calculation, you must create a measure of this real part, imaginary part, modulus or argument and use this measure in the calculation.

You can study another example of complex calculations in this article.

Let us have an example : we want to visualize the image of the cercle of center O and radius 1 by the complexe transformation associated to the complex function f defined by f(z) = z + 1/z^n where n is an integer in the range 1 to 10.

To create a new figure, use icon and ask for an orthonormal frame with vectors. You can get he vectors renamed u and v sif you wish by clicking on icon and clicking on the LaTeX display displaying the vectors.

Use to create the circle of center O and going through point I (I is the point of abscissa 1 on the x-axis. It’s name is hidden).

Use icon 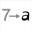to create a variable named n with 1 as mini value, 10 as maxi value, 1 a step value 2 as actual value. Check the checkbox Associated dialog.

Use icon 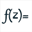to create a complex function of a complexe variable t with formula t+1/t^n.

Expand the displays toolbar and, on the right side click on icon (new macro creation). Choose item Incrementing variable macro. Click on a an empty spot in the top left corner of the figure.

A dialog box pops up. For the tile of the macro use Increment n. The variable n is already selected. Validate by OK.
In the same way, create a macro decrementing variable n with title Decrement n. For this use icon and choose item Decrementing variable macro.

Use icon on the top left orner of the figure a display of the value of variable n (you can use button Values to select n).

With , create a point linked to the circle already created (center O and radius 1) and name this point M.

Expanding the measures toolbar, use icon to measure the affix of point M (just click on M) and name this measure z.

Use icon 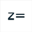to create a complex calculation named z’ with formula f(z).

Use icon to create the point of affix z’ and name this point M’.

All we’ve got to do now is create the locus of point M’generated by the positions of point M on the circle it is linked to.

In the color palette, activate the red color.

Use icon . First click on M’ then on M. In the dialog box popping up, check the checkbox Closed locus and ask for 300 points. Validate.

The figure is ready.

You can see this figure in action underneath :