Toutes les versions de cet article : [English] [Español] [français]
This article has been adapted to the JavaScript version of MathGraph32.
You can also have a look to this video.
MathGraph32 allows you to create recurrent complex suquences type of $u_{n+1}=f(u_n)$ and to graph them.
This article study recurrent complex sequences type of $u_{n + 1} = f\left( {u_n } \right)$ with $f(z) = \frac{1}{2}(z + \frac{a}{z})$.
So the Babylon algorithm is generalized to complex numbers.
Click here to view this article.
Create a new figure with icon  (upper ttolbar) and choose an orthonormal frame with vectors .
(upper ttolbar) and choose an orthonormal frame with vectors .
Use icon  to create a free point and name it M.
to create a free point and name it M.
Expanding the measures toolbar, use icon  to measure the comple affix of point M (just click on M). A dialog box pops up for the choice of the name for this measure. For instance set zM as name and validate.
to measure the comple affix of point M (just click on M). A dialog box pops up for the choice of the name for this measure. For instance set zM as name and validate.
Expand the calculations toolbar and use icon 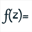 a complex function of a complex variable named f of the t variable defined by the formula f(t)=t+1/t^2.
a complex function of a complex variable named f of the t variable defined by the formula f(t)=t+1/t^2.
Now let us create a xomplex recurrent sequence u type u(n+1)=f[u(n)] first term of which will beeing the complex affix we just measured.
For this, expanding the calculation toolbar, use icon 
A dialog box pops up.
Enter u in the field Nom.
The function f is already selected.
For the first term, use button Values to choose zM is first term.
In the field Number of terms enter 100.
Validate by OK.
Here is the dialog box before validation :
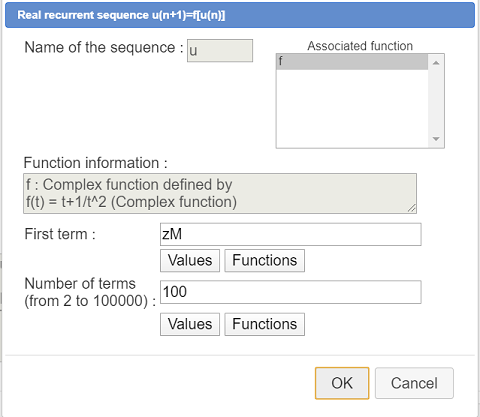
Now let us graph this sequence.
Activate the blue color an the dotted line style.
Then use icon  (graph of a complex recurrent sequence).
(graph of a complex recurrent sequence).
A dialog box pops up :
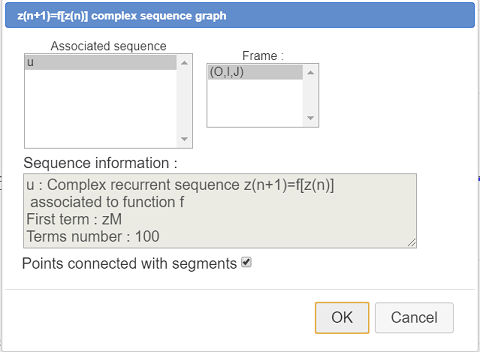
The sequence u is already selected. Validate with the default settings.
Now let us create a formula editor allowing us to modify the formula of f(t) directly on the figure.
Expand the calculations toolbar, use icon  and click on the top left corner of the figure (not too much left).
and click on the top left corner of the figure (not too much left).
A dialog box pops up. Fill in the dialog box as shoxn here (be careful to assign the editor to function f)
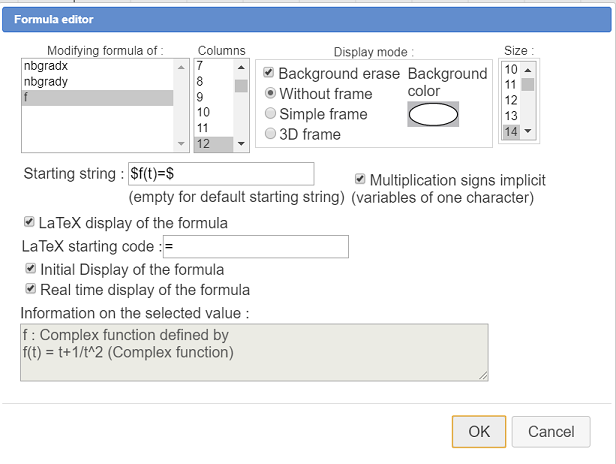
To finish we will display the sequence terms on teh figure.
For this we will use a variable values of which will be in range 0 to 99 (we chose 100 terms for the sequence and indexes start at 0).
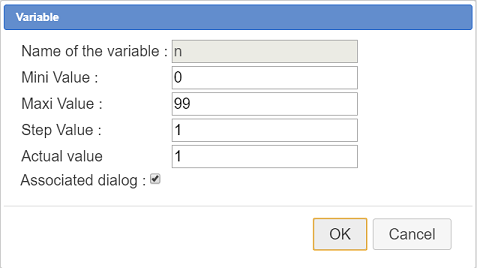
Use  and fill in the dialog box as shown here (variables are always inserted at the beginning of the list of objects). Don’t forget to check the checkbox Associated dialog.
and fill in the dialog box as shown here (variables are always inserted at the beginning of the list of objects). Don’t forget to check the checkbox Associated dialog.
Now expand the calculations toolbar and use use icon  to create a complex calculation named un with formula f(n).
to create a complex calculation named un with formula f(n).
Now let us use a dynamic LaTeX display.
Expand the displays toolbar and use icon  to create a free LaTeX display. Click on te top left side of the figure, under the formula editor. Fill in the dialog box as shown underneath. You ca use the button Value Insertion to insert the special LaTeX code for the display of n and un values (for un ask for 12 digits).
to create a free LaTeX display. Click on te top left side of the figure, under the formula editor. Fill in the dialog box as shown underneath. You ca use the button Value Insertion to insert the special LaTeX code for the display of n and un values (for un ask for 12 digits).
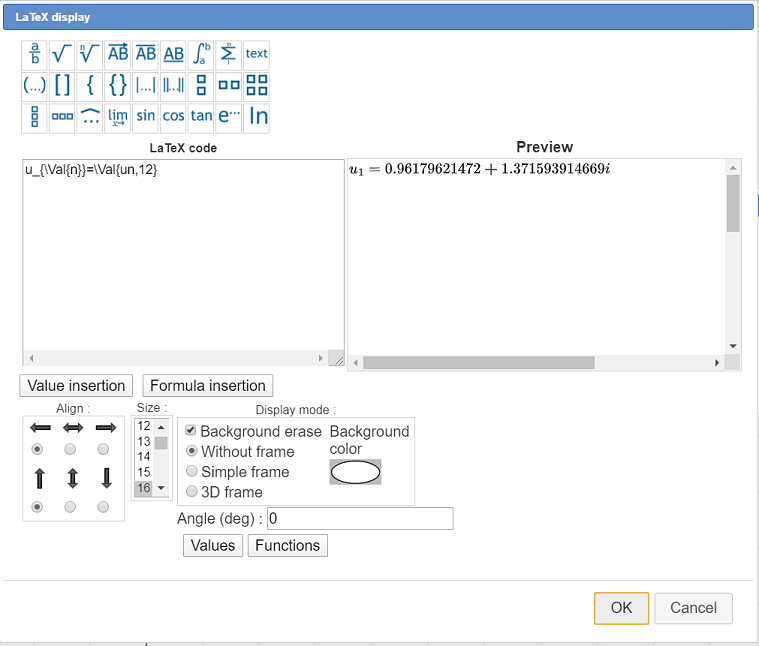
Here is the LaTex code to be used :
The figure is now ready.
You can make values of n vary by clicking on the + and - buttons on the right bottom of the figure.
Underneath you can see this figure.
You can capture point M.
For instance change the formula of f(t) by :
and capture M : the sequence converges toward either 2i or -2i (Babylon complex recurrent sequence).