Toutes les versions de cet article : [English] [Español] [français]
Mostraremos en este artículo cómo usar las construcciones predefinidas de MathGraph32 para representar planos y otros objetos en el espacio.
Este artículo ha sido adaptado a la versión JavaScript de MathGraph32.
Comience creando una figura pseudo 3D provista de un referencial ortonormal con el icono  , elija Figura 3D de base y luego elija el elemento Referencial 3D ortonormal.
, elija Figura 3D de base y luego elija el elemento Referencial 3D ortonormal.
Ahora crearemos cuatro cursores que contendrán los cuatro parámetros de nuestra ecuación del plano $ax+by+cz+d=0$.
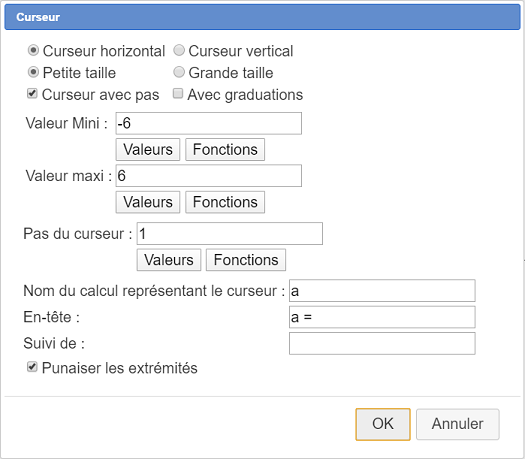
Haga clic en el icono  para crear un cursor. Haga clic en la parte superior izquierda de la figura y complete el cuadro de diálogo como se muestra a continuación. Aquí estamos creando un cursor de valores enteros cuyos valores oscilarán entre -6 y +6.
para crear un cursor. Haga clic en la parte superior izquierda de la figura y complete el cuadro de diálogo como se muestra a continuación. Aquí estamos creando un cursor de valores enteros cuyos valores oscilarán entre -6 y +6.
Nota : Los extremos del cursor están fijados de forma predeterminada. Si desea moverlos o ampliarlo, primero deberá desanclarlos con la herramienta  .
.
Del mismo modo, cree otros tres cursores más de valores enteros (entre -6 y +6) debajo del anterior para los valores de b, c y d.
Con la versión de JavaScript, las macro-construcciones predefinidas deben descargarse por separado del sitio de MathGraph32 en esta página Téléchargement de MathGraph32 version 9.2.
Esto tiene una ventaja : puede agregar macro-construcciones que haya creado usted mismo o eliminar macro-construcciones que considere inútiles.
Por lo tanto, asumiremos que ha descargado la última versión de las construcciones y descomprimido el archivo zip que las contiene en una carpeta de su elección.
Para generar las macroconstrucciones, debemos hacer que aparezcan nuevos íconos en la barra de herramientas superior. Para ello, utilice el icono  .
.
Ahora utilice el icono  (gestión de macro construcciones) y seleccione el ítem Incorporar una construcción desde un archivo. Navegue a la carpeta que contiene las construcciones predefinidas. Abra la carpeta Espacio, luego la subcarpeta Puntos y elija la construcción Representación plano por ecuación.
(gestión de macro construcciones) y seleccione el ítem Incorporar una construcción desde un archivo. Navegue a la carpeta que contiene las construcciones predefinidas. Abra la carpeta Espacio, luego la subcarpeta Puntos y elija la construcción Representación plano por ecuación.
Esta construcción ahora es parte de su figura. Para ver esto, use el ícono  y elija el ítem Modificación de infos de una construcción.
y elija el ítem Modificación de infos de una construcción.
Esta construcción espera cuatro objetos fuentes numéricos que son a, b, c y d y cuatro objetos fuentes gráficos que son los puntos que definen nuestro referencial del espacio : 0, I, J y K.
Nuevamente use el ícono y elija el elemento Implementar una construcción de la figura. Se abre un cuadro de diálogo y nuestra construcción única ya está seleccionada allí. Haga clic en el botón Implementar.
y elija el elemento Implementar una construcción de la figura. Se abre un cuadro de diálogo y nuestra construcción única ya está seleccionada allí. Haga clic en el botón Implementar.
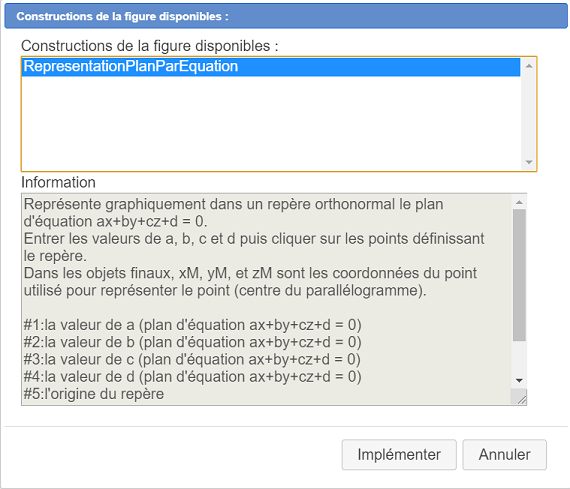
Ahora necesitamos indicarle a nuestra construcción cuáles son los objetos fuentes.
En la lista de la izquierda, haga clic en el número 1. En la lista de la derecha, asócielo con el cálculo a (creado al crear el primer cursor) como se muestra a continuación :
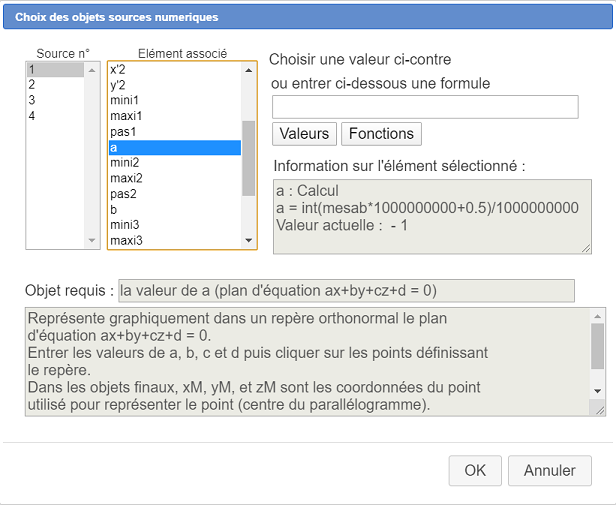
De igual manera asocie a los elementos 2, 3 y 4 los valores de b, c y d luego valide. En la parte superior derecha de la figura, una pantalla fugaz ahora le pide que haga clic en el origen del referencial : haga clic en O. De manera similar, luego haga clic en I, J y K.
El plano está representado por un paralelogramo de color azul (de hecho, es un polígono que se utilizó para crear una superficie). Cuatro puntos de control le permiten ampliar o reducir este polígono. Utilice el icono ![]() para ocultar el punto creado en el centro de este polígono que no se utilizará aquí.
para ocultar el punto creado en el centro de este polígono que no se utilizará aquí.
Con la herramienta de captura ![]() cambie los controles deslizantes para obtener los mismos valores que se muestran a continuación para a, b, c y d (1, 1, 3 y 3) (la figura de abajo es dinámica y puede modificar los valores de a, b, c y d). También puedes girarlo con $\vartheta$.
cambie los controles deslizantes para obtener los mismos valores que se muestran a continuación para a, b, c y d (1, 1, 3 y 3) (la figura de abajo es dinámica y puede modificar los valores de a, b, c y d). También puedes girarlo con $\vartheta$.
Ahora vamos a usar una construcción que permite crear la proyección ortogonal de un punto (aquí el origen) sobre un plano (y proporcionar sus coordenadas que se denominarán en los cálculos xproj, yproj y zproj).
Nuevamente use el ícono  y elija el elemento Incorporar una construcción desde un archivo, abra la carpeta llamada Espacio y luego la subcarpeta Puntos y haga clic en la construcción denominada ProyeccionOrtogonalPuntoSobrePlano. Haga clic en Abrir. como a continuación :
y elija el elemento Incorporar una construcción desde un archivo, abra la carpeta llamada Espacio y luego la subcarpeta Puntos y haga clic en la construcción denominada ProyeccionOrtogonalPuntoSobrePlano. Haga clic en Abrir. como a continuación :
Esta construcción es ahora parte de nuestra figura.
Para implementarla, use nuevamente el ícono  y elija el ítem Implementar una construcción de la figura.
y elija el ítem Implementar una construcción de la figura.
Para el elemento fuente n°1 (abscisa del punto a proyectar) ingrese directamente 0 (abscisa del origen) como se muestra a continuación. Haga lo mismo con los elementos fuentes 2 y 3 (valores 0).
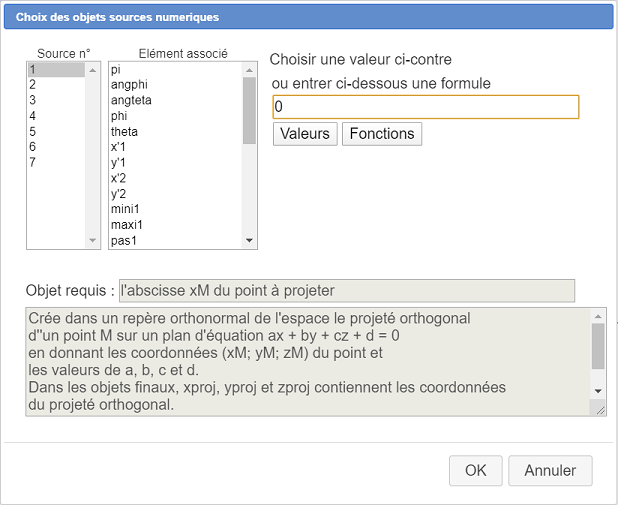
Se nos pide como elemento fuente n° 4 el valor de a : asocie el valor ya existente de la siguiente manera :
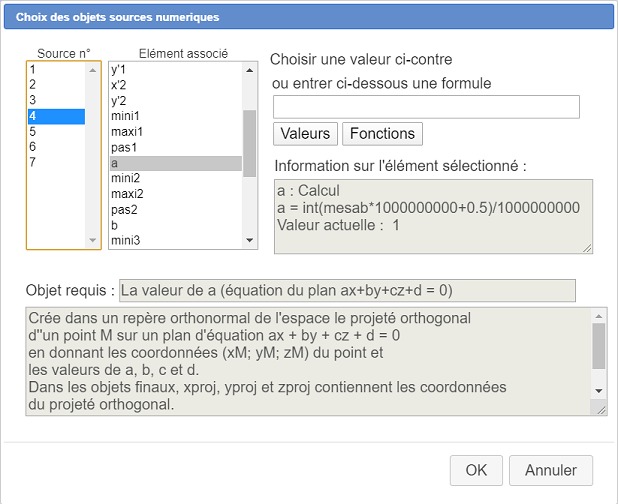
.
Del mismo modo, asocie a los elementos fuente 5, 6 y 7 los cálculos ya existentes b, c y d.
En la parte superior derecha de la figura, una visualización fugaz le pide que haga clic en los cuatro puntos que definen el referencial : haga clic sucesivamente en O, I, J y K.
Aparece un nuevo punto y, en los objetos numéricos, tres cálculos denominados xproj, yproj y zproj contienen las coordenadas de este punto (utilice el icono  para ver todos los objetos de tipo cálculo creados). Nombre a este punto H con la herramienta
para ver todos los objetos de tipo cálculo creados). Nombre a este punto H con la herramienta  .
.
Ahora vamos a simular un punto ligado a nuestro plano. Para ello, utilice el icono  . Primero haga clic en el borde del plano (en realidad es un polígono) y luego dentro de este polígono. Aparece un nuevo punto. Nómbrelo M.
. Primero haga clic en el borde del plano (en realidad es un polígono) y luego dentro de este polígono. Aparece un nuevo punto. Nómbrelo M.
Usemos ahora una construcción predefinida, muy potente, que nos permitirá recuperar las coordenadas de nuestro punto M sabiendo que está en un plano del cual conocemos una ecuación.
Nuevamente use el ícono  y elija el elemento Incorporar una construcción desde un archivo, abra la carpeta llamada Espacio y luego la subcarpeta Puntos y haga clic en la construcción denominada CalculoCoordenadasPuntosEnPlano. Haga clic en Abrir.
y elija el elemento Incorporar una construcción desde un archivo, abra la carpeta llamada Espacio y luego la subcarpeta Puntos y haga clic en la construcción denominada CalculoCoordenadasPuntosEnPlano. Haga clic en Abrir.
En el cuadro de diálogo que se abre, asigne los valores de a, b, c y d a los cuatro objetos fuentes 1, 2, 3 y 4 como antes.
Luego se le pide que haga clic en el punto cuyas coordenadas desea calcular : haga clic en M. Luego haga clic como se indica en los puntos O, I, J y K.
Utilice el icono  de la barra superior. Ir al final de la lista de objetos creados. Los últimos objetos creados son los cálculos que contienen las coordenadas de M y por lo tanto se denominan xM2, yM2 y zM2 como se ve a continuación.
de la barra superior. Ir al final de la lista de objetos creados. Los últimos objetos creados son los cálculos que contienen las coordenadas de M y por lo tanto se denominan xM2, yM2 y zM2 como se ve a continuación.
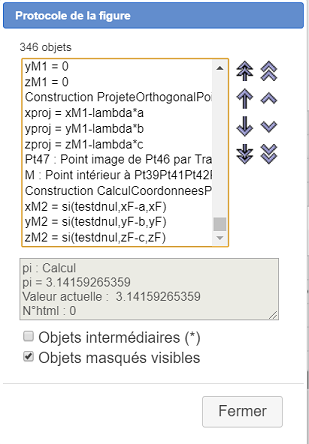
Ahora crearemos una visualización LaTeX responsable de mostrar dinámicamente estas tres coordenadas.
Haga clic en el icono  para crear una visualización de código LaTeX libre y haga clic en la parte superior de la figura en un lugar libre, debajo de los cursores.
para crear una visualización de código LaTeX libre y haga clic en la parte superior de la figura en un lugar libre, debajo de los cursores.
En la ventana que aparece, escriba la letra M y luego haga clic en el icono  . <Aparece el código LaTeX correspondiente a un paréntesis de apertura :
. <Aparece el código LaTeX correspondiente a un paréntesis de apertura : M\left( { } \right) y el cursor parpadea dentro de la llave. Luego haga clic en el botón Insertar valor.
Complete el cuadro de diálogo de la siguiente manera :
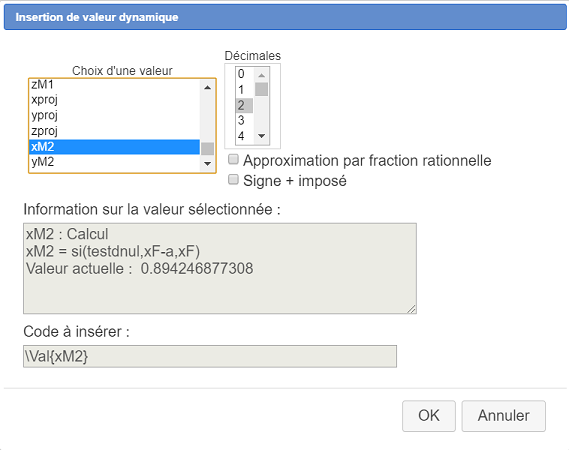
Validar. Inmediatamente después, escriba un carácter punto y coma.
El código LaTex ahora es : M\left( {\Val{xM2}; } \right).
Luego use el botón Inserción de valor de la misma manera para insertar una visualización de los valores de xM2 y yM2 con un separador de punto y coma.
Haga lo mismo para obtener una visualización dinámica de los valores de yM2 y zM2 después de los punto y coma.
Por el momento nuestro código LaTeX es :
M \left( \Val{xM2}; \Val{yM2}; \Val{zM2} \right).
Queremos que la M no se muestre en cursiva : seleccione la M en el editor y luego haga clic en el icono 
El código LaTeX ahora es el siguiente. Marque las casillas Borrado de fondo y Marco simple.
\text{M} \left( \Val{xM2}; \Val{yM2}; \Val{zM2} \right)
Valide el cuadro de diálogo. Aparece nuestra pantalla y si captura M verá sus coordenadas actualizadas.
Proceda de la misma manera para mostrar debajo de la visualización LaTeX anterior a la visualización de las coordenadas de H. El código LaTeX obtenido debe ser el siguiente :
\text{H} \left( \Val{xproj}; \Val{yproj}; \Val{zproj} \right)
Ahora le pediremos al software que calcule la distancia entre O y M utilizando una construcción predefinida (por supuesto, podríamos calcularla directamente).
Esta vez nuevamente, use el ícono  , elija el ítem Incorporar una construcción desde un archivo e incorpore la construcción llamada Distancia Punto Punto que encuentra en la carpeta Espacio -> Distancias.
, elija el ítem Incorporar una construcción desde un archivo e incorpore la construcción llamada Distancia Punto Punto que encuentra en la carpeta Espacio -> Distancias.
Luego use el ícono  nuevamente y elija el elemento Implementar una construcción de la figura. Elija esta última construcción de Distancia Punto Punto de la lista y haga clic en el botón Implementar.
nuevamente y elija el elemento Implementar una construcción de la figura. Elija esta última construcción de Distancia Punto Punto de la lista y haga clic en el botón Implementar.
Como objetos fuentes 1, 2 y 3, ingrese directamente como fórmula 0 en el campo de edición (coordenadas del origen) y asigne como objetos fuentes 4, 5 y 6 respectivamente xM2, yM2 y zM2 (coordenadas de M). Se creó un objeto final llamado dist que contiene la distancia entre O y M. Puede ver esto con la herramienta de la barra superior.
de la barra superior.
Ahora crearemos una visualización de este valor. Para hacer esto, use el ícono ![]() luego haga clic debajo de las dos visualizaciones anteriores.
luego haga clic debajo de las dos visualizaciones anteriores.
Complete el cuadro de diálogo como se muestra a continuación (puede usar el botón Valores).
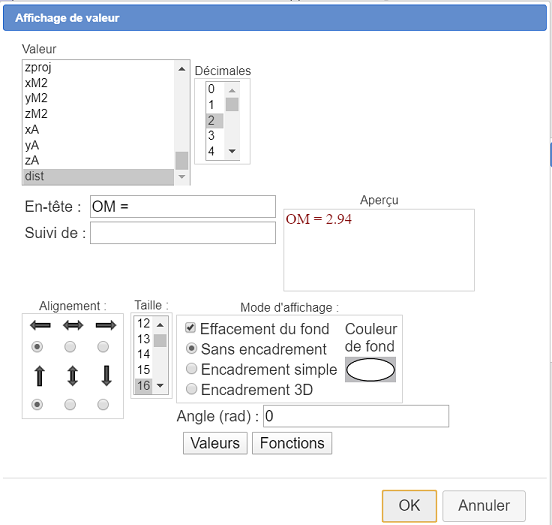
Del mismo modo utilice la misma construcción predefinida para calcular la distancia entre O y H (recuerde que las de H están contenidas en xproj, yproj y zproj) y cree una visualización de este valor (dist1) a continuación a partir de la visualización anterior.
Nuestra figura es ahora la de abajo. Capture $\theta$ para rotar la figura, el punto M o hacer variar los valores de a, b, c y d.
Ahora vamos a utilizar construcciones predefinidas para representar la esfera de centro O y que pasa por M y la circunferencia de intersección de esta con nuestro plano.
Esta vez nuevamente, use el ícono  , elija el elemento Incorporar una construcción desde un archivo e incorpore la construcción llamada EsferaPorCoordCentroRadio que se encuentra en la carpeta Espacio -> Sólidos.
, elija el elemento Incorporar una construcción desde un archivo e incorpore la construcción llamada EsferaPorCoordCentroRadio que se encuentra en la carpeta Espacio -> Sólidos.
Proceda de la misma forma para incorporar en la figura la construcción CircunferenciaIntersecciónEsfera Plano que encontrará en la carpeta Rectas Circunferencias.
Comencemos creando la esfera de centro O y que pasa por M.
Utilice el icono  , elija el elemento Implementar una construcción de la figura. Elija la construcción EsferaPorCoordCentroRadio y haga clic en el botón Implementar.
, elija el elemento Implementar una construcción de la figura. Elija la construcción EsferaPorCoordCentroRadio y haga clic en el botón Implementar.
Se abre un cuadro de diálogo para elegir los objetos fuentes numéricos. Para los tres primeros objetos fuentes, asigne como fórmula 0 (coordenadas de O). Establezca el número de objeto fuente número 4 dist (distancia de O a M) como se muestra a continuación.
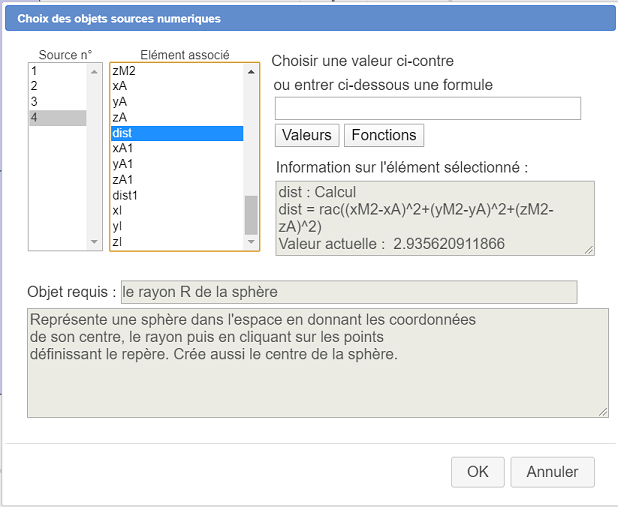
Luego se le pide que haga clic en los cuatro puntos que definen el referencial : haga clic en O, I, J y K. Aparece la representación de la esfera (ella está compuesta por lugares geométricos de objetos).
Representemos ahora gráficamente la circunferencia de la intersección de la esfera con el plano.
Utilice el icono  , elija el elemento Implementar una construcción de la figura. Elija la construcción CircunferenciaIntersecciónEsferaPlano y haga clic en el botón Implementar.
, elija el elemento Implementar una construcción de la figura. Elija la construcción CircunferenciaIntersecciónEsferaPlano y haga clic en el botón Implementar.
Asigne como valor para los primeros tres objetos fuentes 0 usando el campo Fórmula (coordenadas del centro de la esfera). Como elemento asociado con el objeto fuente n.° 4, haga clic en dist. Como elementos asociados a los objetos fuentes números 5, 6, 7 y 8, haga clic en a, b, c y d. Validar.
Luego se le pide que haga clic en los cuatro puntos que definen el referencial : haga clic en O, I, J y K (para O elija el punto libre).
Aparece un lugar geométrico de puntos que representa la circunferencia de la intersección.
Puede cambiar su color y estilo de línea con la herramienta  y rellenarlo de color con la herramienta
y rellenarlo de color con la herramienta 
Por último, active el estilo de línea punteada, de 2 píxeles de grosor, el color azul y utilice el icono  para unir los puntos O, H y M mediante tres segmentos. El triángulo OHM es rectángulo en H y H es el centro de la circunferencia de intersección.
para unir los puntos O, H y M mediante tres segmentos. El triángulo OHM es rectángulo en H y H es el centro de la circunferencia de intersección.
A continuación se muestra la figura final :
Vous pouvez récupérer ci-dessous le code Base 64 de cette figure :