Toutes les versions de cet article : [English] [Español] [français]
Al poner a prueba el software MathGraph32 me encontré con resultados inesperados. Esta es la prueba de que todavía se puede hacer descubrimientos matemáticos utilizando un software de este tipo.
El primero se refiere a las propiedades de un una transformación baricéntrica del plano (un artículo apareció en el boletín de la APMEP al respecto). Usted puede encontrar una descripción completa en el sitio del CNDP en la siguiente dirección : http://www.cndp.fr/maths y haciendo clic en la pestaña teorema descubierto a través de MathGraph32. Este primer resultado es totalmente original. El resultado fundamental procede del teorema de Ptolomeo.
El segundo se refiere a un tipo particular de sucesión recurrente compleja. Yo "tropecé" con este resultado comprobando el funcionamiento de MathGraph32 con los números complejos. No certifico que este segundo resultado sea original, pero hasta ahora para la gente quien yo lo presenté no era conocido.
Un resultado conocido está en el hecho que, si p es un real positivo, la sucesión real definida por su primer término $u_0$ y la relación de recurrencia $u_{n+1}=\frac{1}{2}\left( u_n+\frac{p}{u_n} \right)$ converge hacia $\sqrt{p}$ (este resultado es conocido desde la antigüedad para p=2 con el nombre de algoritmo de Babilonia).
Nos ocuparemos de la sucesión recurrente compleja $(z_n)$ cuyo primer término es un complejo $z_0$
MathGraph32 nos ayudará a examinar visualmente una tal sucesión y realizar conjeturas. Propondremos al final de este artículo demostraciones de los resultados observados, a continuación, una generalización.
Creación de dos figuras que ilustran esta situación con MathGraph32.
Comience MathGraph32 y utilice el icono ![]() para crear una nueva figura proporcionada munida de un referencial. Como el tipo de cuadrícula, marque AvecPointillés. Marque la casilla Repère avec vecteurs e ingrese u y v como nombre de los vectores. Valide.
para crear una nueva figura proporcionada munida de un referencial. Como el tipo de cuadrícula, marque AvecPointillés. Marque la casilla Repère avec vecteurs e ingrese u y v como nombre de los vectores. Valide.
Con la ayuda del icono ![]() , cree un punto libre. Utilice el icono
, cree un punto libre. Utilice el icono ![]() para nominar ese punto
para nominar ese punto
Deseamos medir el afijo de ese punto en nuestro referencial. Para ello utilice el icono ![]() .
.
Cliqueamos sobre el punto $M_0$. Un mensaje nos confirma la creación de ese afijo.
Para mayor comodidad, se define un cálculo complejo nominado z0 que contendrá el afijo medido previamente.
Utilizamos para ello el menú Cálculos - Nuevo cálculo en C - Cálculo complejo (atajo de teclado : Ctrl + Maj + E).
Se abrirá un cuadro de diálogo. En el campo Nombre del cálculo, introduzca z0. Utilice el botón Valores para entrar en el campo la fórmula Aff(M0,O,I,J) que representa al afijo que hemos medido. Confirme con OK.
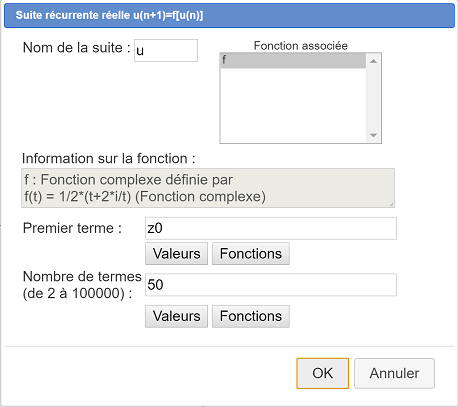
Vamos a definir la sucesión recursiva compleja $\left( z_n \right)$ de primer término $z_0$ dado y definida por la relación de recurrencia $z_n+1=\frac12\left( z_n+\frac2iz_n \right)$.
Antes de eso, necesitamos crear una función compleja f de una variable compleja definida por $f(t)=\frac{1}{2}\left(t+\frac{2i}{t}\right)$.
Se utiliza el menú Cálculos - Nuevo cálculo en C >> Función compleja (atajo teclado : Ctrl + G).
Se abrirá un cuadro de diálogo. Ingresamos f en el campo Nombre de la función y t en el campo Variable formal. En el campo Fórmula, ingresamos 1/2*(t+2*i/t). Validamos con OK.
Creamos ahora la sucesión recurrente.
Se utiliza para ello el menú Cálculos >> Nuevo cálculo en C >> Sucesión compleja u(n+1) = f[u(n)]. Se abrirá un cuadro de diálogo. La completamos como sigue.
Ahora vamos a crear la gráfica de esta sucesión recurrente compleja. Cada término de la sucesión se indica con una marca de puntos y estas marcas de puntos estarán unidas por segmentos.
En la paleta de colores, activamos el azul y luego el estilo de línea punteado en la paleta de estilo de trazo.
En la paleta de estilo de punto, activamos « pequeño, redondo » (esto no es indispensable).
Utilizamos el menú Crear >> Gráfico de una sucesión - Compleja. La gráfica aparece.
Utilizamos el icono ![]() para capturar el punto $M_0$.
para capturar el punto $M_0$.
La figura obtenida se muestra a continuación animada por el motor de JavaScript de MathGraph32. (Podemos capturar el punto $M_0$).
Por la figura anterior, la sucesión parece converger a 1 + i. Para otras posiciones de $M_0$, la sucesión parece converger hacia – 1 – i.
¿Es sorprendente si se recuerda que 1 + i et – 1 – i son los dos complejos cuyo cuadrado es 2i ?
Cuando el punto $M_0$ se aproxima a la recta de ecuación y = – x, aparece un comportamiento especial. Estudiémoslo con MathGraph32.
En la paleta de colores, activamos el negro.
Dibujemos en primer lugar la recta de ecuación y = – x (que llamaremos D). Para ello utilizamos el icono ![]() de creación de una recta por su coeficiente director.
de creación de una recta por su coeficiente director.
Cliqueamos seguidamente sobre el punto O.
En la caja de diálogo que se abre, ingresamos – 1 en el campo Coeficiente director. Validamos por OK. La recta aparece.
Capturando el punto $M_0$, se observa que, cuando $M_0$ no está sobre la recta D, todos los puntos de la gráfica de la sucesión parecen quedar en el mismo semiplano de borde D que el punto $M_0$.
Veamos ahora lo que pasa cuando $M_0$ está sobre la recta D.
Utilizamos para ello el menú Modificar - Creación de una ligadura - Entre un punto y un objeto. Cliqueamos sobre el punto $M_0$, luego sobre la recta D. El punto $M_0$ queda ahora ligado a la recta D.
La siguiente es la figura obtenida (Se puede capturar el punto $M_0$) :
Capturemos el punto $M_0$ con la ayuda del icono ![]() . Parecería que todos los puntos de afijo $z_n$ quedan sobre la recta D y que el comportamiento de esta sucesión es « caótica ».
. Parecería que todos los puntos de afijo $z_n$ quedan sobre la recta D y que el comportamiento de esta sucesión es « caótica ».
Justificación matemática de los resultados observados más arriba
El resto de este artículo puede ser leído por un estudiante de bachillerato científico admitiendo que :
– Una sucesión $\left( z_n \right)$ de números complejos converge hacia un complejo $\ell$ cuando $\lim_{n \to {+\infty }} \left| z_n - \ell \right| = 0$.
– Los teoremas usuales concernientes a las operaciones sobre las sucesiones convergentes en R se generalizan a C.
Pongamos a = 1+ i y b = –a = –1 – i. Llamemos A y B a los puntos de afijos respectivos a y b = – a.
Para todo natural n, se tiene : $z_{n+1}-a = \frac{1}{2}\left( z_n + \frac{a^2 }{z_n } \right)-a=\frac{1 }{2 }\left( \frac{{z_n}^2+a^2-2az_n }{ z_n} \right)=\frac{1 }{2z_n }\left( z_n-a \right)^2$.
Y análogamente se obtiene $z_{n+1}-b ==\frac{1 }{2z_n }\left( z_n-b \right)^2$.
Se deduce entonces que $\frac{z_{n+1}-a }{z_{n+1} + a } = \left( \frac{z_n-a }{z_n+a } \right)^2$.
Se puede entonces mostrar por recurrencia que, para todo natural n, $\left( \frac{z_n-a }{z_n+a } \right)=\left( \frac{z_0-a }{z_0+a } \right)^{2^n}$. Se deduce que $\left| \frac{z_n-a }{z_n+a } \right|=\left| \frac{z_0-a }{z_0+a } \right|^{2^n}$.
Supongamos que el punto $M_0$ está en el semiplano abierto de frontera D que contiene a A. Eso quiere decir que $M_0$ está más próximo de A que de B es decir que $\left| z_0-a \right| < \left| z_0-b \right| $y entonces que $\left| \frac{z_0-a }{z_0+a } \right| < 1$. Se deduce entonces que $\lim_{n \to {+\infty }}\left| \frac{z_n-a }{z_n+a } \right| = 0$ y que la sucesión de complejos $\left( \frac{z_n-a }{z_n+a } \right)$ converge hacia 0.
Ahora $\frac{z_n-a }{z_n+a }=\frac{z_n+a-2a }{z+a }=1-\frac{2a }{z_n+a }$ lo que implica que $z_n+a=\frac{2a }{1-\frac{z_n-a }{z_n+a } }$. Aplicando los teoremas relativos a las operaciones sobre los límites, se deduce que $(z_n + a)$ converge hacia $2a$ y por lo tanto que $(z_n)$ converge hacia a.
El exponente $2^n$ explica la extrema rapidez de la convergencia de la sucesión hacia a = 1 + i.
Se muestra de la misma manera que cuando $M_0$ está en el semiplano abierto de frontera D que contiene a A, la sucesión converge hacia b = – a.
Interesémonos ahora en lo que pasa cuando el punto $M_0$ está sobre la recta D.
Llamemos $M_n$ al punto de afijo $z_n$.
Mostremos primeramente que cuando el punto $M_n$ está sobre D, el punto $M_{n+1}$ está también sobre D.
Si $M_n$ está sobre D, es que $zn$ es de la forma $z_n = xia$ con x real (en efecto el vector de afijo i.a es ortogonal al vector $\overrightarrow{OA}$ de afijo a).
Se tiene entonces $z_{n+1}=\frac{1 }{2 }\left( xia+\frac{a^2 }{xia } \right)=\frac{1 }{2 }\left( xia-i\frac{a }{x } \right)=\frac{1 }{2 }\left( x-\frac{1 }{x } \right)\times ia$,lo que prueba que $M_{n+1}$ está también sobre D.
Por recurrencia se deduce entonces que todos los puntos $M_n$ están sobre D.
Pongamos ahora $z_n = x_n ia$. Se tiene entonces, para todo n, $x_{n+1}=\frac{1 }{2 }\left( x_n - \frac{1 }{x_n } \right)$.
MathGraph32 va ahora a ayudarnos a explicar el comportamiento caótico de la sucesión de puntos $M_n$ cuando $M_0$ está sobre D.
Iniciemos MathGraph32 y utilicemos el ícono ![]() y demandemos un referencial ortonormal no cuadriculado y sin vectores.
y demandemos un referencial ortonormal no cuadriculado y sin vectores.
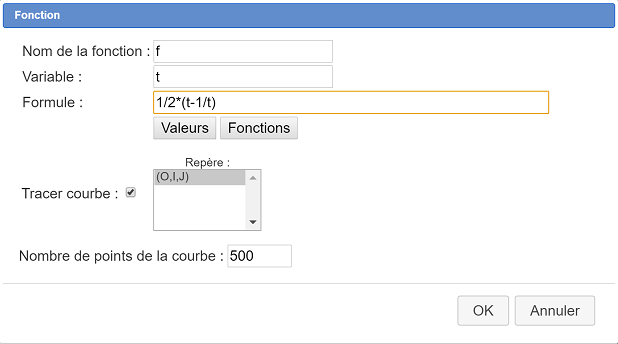
Utilicemos el ícono ![]() para crear una función f definida por $f(t) = \frac{1}{2} \left( t - \frac{1}{t} \right)$.Completemos la caja de diálogo como se ve a continuación. Dejemos marcada la casilla trazar curva y validemos.
para crear una función f definida por $f(t) = \frac{1}{2} \left( t - \frac{1}{t} \right)$.Completemos la caja de diálogo como se ve a continuación. Dejemos marcada la casilla trazar curva y validemos.
Tracemos ahora la recta de ecuación y = x con la ayuda del icono ![]() de creación de una recta por su ecuación (atajo Ctrl + Q). Ingresemos
de creación de una recta por su ecuación (atajo Ctrl + Q). Ingresemos y=x en el campo Ecuación y validemos por OK.
En la paleta de colores, activamos el color rojo.
Utilicemos el icono ![]() de creación de un punto ligado para crear un punto ligado al eje de las abscisas. Utilicemos el icono
de creación de un punto ligado para crear un punto ligado al eje de las abscisas. Utilicemos el icono ![]() para nominar a ese punto x0.
para nominar a ese punto x0.
Cliqueamos sobre el icono ![]() que se usa para medir la abscisa de un punto en un referencial. Cliqueamos sobre el punto x0. Un mensaje nos confirma la creación de esa medida que es denotada xCoord(x0,O,I,J).
que se usa para medir la abscisa de un punto en un referencial. Cliqueamos sobre el punto x0. Un mensaje nos confirma la creación de esa medida que es denotada xCoord(x0,O,I,J).
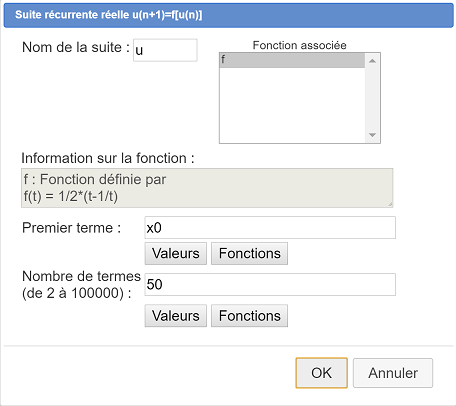
Creamos ahora la sucesión recurrente vía el menú Cálculos - Nuevo cálculo en R - Sucesión real u(n+1)=f[u(n)].
Como Nombre de la sucesión, ingresamos u. Utilizamos el botón Valores para entrar xCoord(x0,O,I,J) en el campo Primer término. Entramos 50 en el campo Número de términos luego validamos con OK. Vemos la caja de diálogo siguiente.
Ahora vamos a crear la gráfica de esta sucesión.
En la paleta de estilo de trazo, activamos el estilo de trazo punteado.
Utilizamos el menú Crear - Gráfico de una sucesión recurrente - Real. Una caja de diálogo se abre. Dejamos marcada la casilla Trazos indicadores en abscisas y validamos con OK.
Podemos ahora capturar el punto x0 con la ayuda del icono ![]() para constatar que el comportamiento de la sucesión parece caótica cualquiera que sea su primer término.
para constatar que el comportamiento de la sucesión parece caótica cualquiera que sea su primer término.
Aquí está la figura obtenida (Se puede capturar el punto x0) :
Tratemos de explicar este fenómeno caótico :
La sucesión no puede converger a un real no nulo L porque de lo contrario, siendo f continua en L se verificaría $f(L)=L\Leftrightarrow L-\frac{1 }{L }=L\Leftrightarrow -\frac{1 }{L }=0$ lo que es imposible.
Es evidente que, para x > 0, se tiene f(x) < x y que, para x < 0, se tiene f(x)>x. Se deduce que si, por ejemplo, el primer término de la sucesión es positivo, la sucesión va a comenzar a decrecer con términos positivos. Pero como la sucesión no puede converger, ella no puede ser acotada (teorema de la convergencia monótona). Habrá entonces a partir de un cierto rango un término que será negativo. Entonces a partir de ese término la sucesión se pondrá a crecer con términos negativos. Pero como ella no es convergente ella no está acotada superiormente y a partir de un cierto rango un término se convertirá positivo y así sucesivamente.
También se puede observar que para ciertos valores del primer término $x_0$ , la sucesión puede no estar definida, por ejemplo para $x_0 = 0$, o para $x_0=-1$.
Los resultados anteriores se pueden generalizar fácilmente con la sucesión definida por $z_{n+1}=\frac{1 }{2 }\left( z_n+\frac{a^2 }{z_n } \right)$ donde a designa un complejo no nulo. En efecto nuestros cálculos anteriores no utilizaron el valor particular de a.
Llamando A al punto de afijo a y B al punto de afijo - a, D la mediatriz de un segmento [AB] (D tiene un vector director de afijo ia), los resultados precedentes son todavía verdaderos :
Si la sucesión está bien definida :
Si $M_0$ está en el semiplano abierto de borde D que contiene a A, la sucesión converge hacia a.
Si $M_0$ está en el semiplano abierto de borde D que contiene a B, la sucesión converge hacia –a.
Si $M_0$ está sobre la recta D entonces todos los puntos $M_n$ d’affixe $z_n$ están sobre esa recta con un comportamiento caótico..
Ilustremos este resultado general, con una nueva figura MathGraph32. La construcción será al comienzo idéntica a nuestra primera figura.
Iniciemos MathGraph32 y utilicemos el icono ![]() para crear un referencial ortonormal, punteado y con vectores nominados u y v.
para crear un referencial ortonormal, punteado y con vectores nominados u y v.
En la paleta de colores, activamos el color rojo.
Con la ayuda del icono ![]() , creamos un punto libre. Utilizamos el icono
, creamos un punto libre. Utilizamos el icono ![]() para nominar ese punto $M_0$.
para nominar ese punto $M_0$.
Ahora medimos el afijo de este punto en nuestro referencial. Para ello, utilizamos el icono ![]() . Cliqueamos sobre el punto $M_0$. Un mensaje nos confirma la creación de este afijo.
. Cliqueamos sobre el punto $M_0$. Un mensaje nos confirma la creación de este afijo.
Para mayor comodidad, ahora tenemos un cálculo complejo llamado z0 que contiene al afijo medido previamente.
Utilizamos para ello el menú Cálculos - Nuevo cálculo en C - Cálculo complejo (atajo teclado : Ctrl + Maj + E).
Se abre una caja de diálogo. En el campo Nombre del cálculo, ingresamos z0. Utilizamos el botón Valores para entrar en el campo fórmula Aff(M0,O,I,J) que representa al afijo que venimos de medir. Validamos por OK.
En la paleta de colores, activamos el color negro.
Con la ayuda del icono ![]() , creamos otro punto libre.
, creamos otro punto libre.
Utilizamos el icono ![]() para nominar ese punto A.
para nominar ese punto A.
Utilizamos el icono ![]() para crear la imagen del punto A en la simetría central de centro O (para ello cliqueamos primero sobre el punto O y luego sobre A).
para crear la imagen del punto A en la simetría central de centro O (para ello cliqueamos primero sobre el punto O y luego sobre A).
Nominemos a ese punto B.
Utilizamos el icono ![]() para crear el segmento [AB] luego el icono
para crear el segmento [AB] luego el icono ![]() para crear la mediatriz del segmento [AB].
para crear la mediatriz del segmento [AB].
Midamos ahora al afijo de ese punto A (icono ![]() y clic sobre A).
y clic sobre A).
Vamos a crear un cálculo complejo nominado a que contendrá al afijo precedentemente medido.
Utilizamos para ello el menú Cálculos - Nuevo cálculo en C - Cálculo complejo (atajo teclado : Ctrl + Maj + E).
Una caja de diálogo se abre. En el campo Nombre del cálculo , ingresamos a. Utilizamos el botón Valores para entrar en el campo fórmula Aff(A,O,I,J) que representa al afijo que acabamos de medir. Validamos por OK.
Debemos crear una función compleja f de una variable compleja definida por $f(t)=\frac{1}{2}\left( t+\frac{a^2}{t} \right)$.
Utilizamos para ello el menú Cálculos - Nuevo cálculo en C - Función compleja .
Una caja de diálogo se abre. Ingresamos f en el campo Nombre de la función y t en el campo Variable formal. En el campo Fórmula, entramos 1/2*(t+a^2/t). Validamos porOK.
Creamos ahora la sucesión recurrente.
Utilizamos para ello el menú Cálculos - Nuevo cálculo en C - Sucesión compleja u(n+1) = f[u(n)]. Una caja de diálogo se abre. La completamos como se ve a continuación.
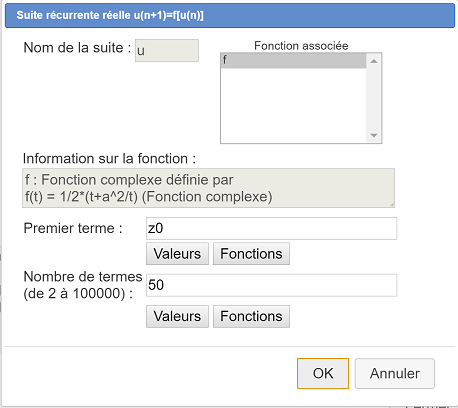
En el campo Nombre de la sucesión, entramos z. En la lista de las funciones complejas existentes, la función f ya está seleccionada. Utilizamos el botón Valores para entrar z0 en el campo Primer término. Entramos 50 como número de términos y validamos con OK.
Vamos ahora a crear la gráfica de esta sucesión recurrente compleja.
En la paleta de colores, activamos el azul y activamos trazo punteado en la paleta de estilo de trazo .
En la paleta de estilo de punto, estilo el « pequeño redondo » (esto no es indispensable).
Utilizamos ahora el menú Crear >> Gráfico de una sucesión recurrente - Compleja y pedimos el gráfico de la sucesión z. El gráfico aparece.
Podemos ahora capturar al punto A y al punto $M_0$ y constatamos que el resultado anterior se generaliza bien.
Aquí está la figura obtenida (Podemos capturar el punto A y el punto $M_0$) :
Observemos ahora que es lo que pasa cuando se está sobre la mediatriz del segmento [AB].
Utilizamos el icono ![]() para crear la mediatriz del segmento [AB].
para crear la mediatriz del segmento [AB].
Liguemos ahora el punto $M_0$a esa mediatriz (menú Modificar - Crear una ligadura - Entre un punto y un objeto luego clic sobre la mediatriz).
Constataremos que todos los puntos de la representación gráfica de la sucesión (puede ocurrir que algunos puntos se apartan de la recta : esto se debe a fenómenos de acumulación de errores de redondeo).
Esta es la figura obtenida (Podemos capturar el punto A y el punto $M_0$.) :
Hemos visto en este ejemplo que MathGraph32 es una herramienta muy útil para realizar figuras sofisticadas en unos pocos clics del mouse. Queda luego el placer de tratar de demostrar lo que se ha observado..
MathGraph32 es por tanto una herramienta especialmente adecuada para los pruebas prácticas en las clases de bachillerato de la opción científica, gracias a su capacidad de calcular con números complejos y representarlos gráficamente
La práctica regular de una herramienta de este tipo debería fomentar en nuestros alumnos el placer de la conjetura y la experiencia desde el colegio. (MathGraph32 puede adaptarse a nivel de colegio mediante la elección este modo en el menú Preferencias. >> Nivel).
Yves Biton (autor de MathGraph32)