Toutes les versions de cet article : [English] [Español] [français]
Dans cet article je vais montrer comment illustrer le TP4 du livre de Terminale S édité par Magnard (premier livre de TS sous licence libre), l’association Sesamath étant chargée du manuel numérique : Cliquez sur ce lien pour lire le texte de ce TP.
Il s’agit donc de visualiser l’ensemble des points d’affixe z0 tels que la suite récurrente définie par $z_{n+1}=z_n^2-1$ soit bornée et de visualiser le comportement d’une telle suite suivant son premier terme.
Voici ci-dessous la figure que nous souhaitons obtenir, animée par le moteur JavaScript de MathGraph32. Vous pouvez capturer le point M et cliquer sur les boutons + et - pour visualiser les 50 premiers termes de la suite.
A noter que la figure est plus fluide avec les navigateur Chrome ou Edge (tous les deux basés sur Chromium maintenant).
Les explications qui suivent ont été adaptées à la version JavaScript de MathGraph32.
Les icônes sont maintenant regroupées par type.
Du haut bers le bas :
– Icônes de création de points
– Icônes de création de droites
– Icônes de création de segments, demi-droites, vecteurs.
– Icônes de création de cercles et arcs de cercles.
– Icônes de création de polygones.
– Icônes de création de marques (de segments et d’angles).
– Icônes de création de lieux de points, courbes, lieux d’objets.
– Icônes de création de transformations.
– Icônes de mesures.
– Icônes de création d’affichages.
– Icônes de création de calculs.
– Icônes de création de surfaces.
Commencez par utiliser l’outil  de la barre supérieure pour créer une nouvelle figure et choisissez Figure avec repère.
de la barre supérieure pour créer une nouvelle figure et choisissez Figure avec repère.
Choisissez un repère orthonormal non quadrillé et sans graduations.
A l’aide de l’outil de capture ![]() éloignez le point I du point O comme sur la figure ci-dessus.
éloignez le point I du point O comme sur la figure ci-dessus.
A l’aide de l’icône
Dans la palette de couleurs, activez la couleur bleue.
Avec l’outil  (en déroulant la barre d’outils des transformations), créez les images H’ et K’ de H et de K dans la symétrie centrale de centre O (cliquez d’abord sur le point O, centre de la symétrie, puis sur les points H et K).
(en déroulant la barre d’outils des transformations), créez les images H’ et K’ de H et de K dans la symétrie centrale de centre O (cliquez d’abord sur le point O, centre de la symétrie, puis sur les points H et K).
Utilisez l’icône  pour joindre les points K et K’ par un segment.
pour joindre les points K et K’ par un segment.
Avec l’outil  créez un point lié au segment [KK’] que vous nommerez P.
créez un point lié au segment [KK’] que vous nommerez P.
Utilisez maintenant l’outil  pour créer les images Q et Q’ des points H et H’ par la translation de vecteur $\overrightarrow{OP}$ (pour cela cliquez d’abord sur les points O et P puis sur les points H et H’).
pour créer les images Q et Q’ des points H et H’ par la translation de vecteur $\overrightarrow{OP}$ (pour cela cliquez d’abord sur les points O et P puis sur les points H et H’).
Joignez les points Q et Q’ par un segment (icône  ).
).
Dans la palette de couleurs, activez la couleur rouge et, avec l’icône  , créez un point lié au segment [QQ’] que vous nommerez M0.
, créez un point lié au segment [QQ’] que vous nommerez M0.
Nous allons maintenant demander au logiciel de mesurer l’affixe du point M0 dans le repère (O ;I,J). Pour cela déroulez la barre des icônes de mesure, utilisez l’icône  et cliquez sur le point M. Un boîte de dialogue s’ouvre : Entrez u0 comme nom pour cette affixe et validez.
et cliquez sur le point M. Un boîte de dialogue s’ouvre : Entrez u0 comme nom pour cette affixe et validez.
Pour créer une suite récurrente complexe il faut d’abord créer une fonction complexe d’une variable complexe. Utilisez l’icône 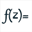 (qui se trouve dans les icônes de calcul, troisième rangée d’icônes en partant du bas) et remplissez la boîte de dialogue comme ci-dessous.
(qui se trouve dans les icônes de calcul, troisième rangée d’icônes en partant du bas) et remplissez la boîte de dialogue comme ci-dessous.
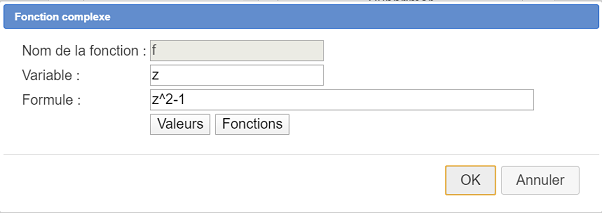
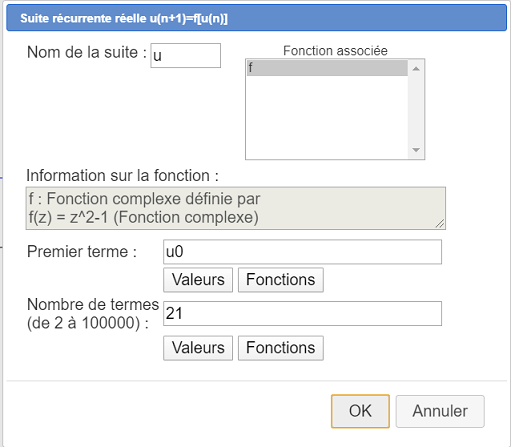
Pour créer la suite récurrente, utilisez l’icône 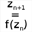 (même rangée d’icônes que précédemment) et remplissez la boîte de dialogue comme ci-dessous :
(même rangée d’icônes que précédemment) et remplissez la boîte de dialogue comme ci-dessous :
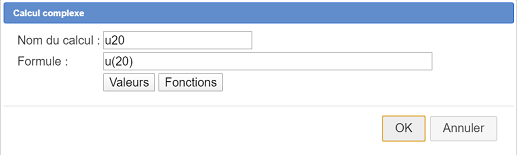
Utilisez maintenant l’icône  pour créer une calcul complexe nommé u20 avec comme formule
pour créer une calcul complexe nommé u20 avec comme formule u(20) comme ci-dessous.
Remarque : Il se peut que le logiciel vous avertisse que ce calcul n’existe pas (pour des raisons de dépassement de capacité de calcul). Si c’est le cas, acceptez quand même la création et rapprochez le point M0 du point P et le point P du point O. Vérifiez alors avec la touche de fonction F3 que le calcul u20 existe bien (icône  ).
).
Nous allons maintenant créer un test d’existence.
Pour cela déroulez la barre des calculs et cliquez à sa droite sur l’icône  qui faire apparaître une boîte de dialogue.
qui faire apparaître une boîte de dialogue.
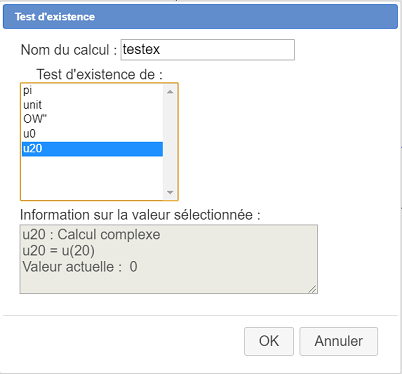
Dans la liste proposée, choisissez Test d’existence pour créer un test d’existence nommé testex de la valeur de u20 : Si le calcul u20 existe, testex vaudra 1 et sinon il vaudra 0. Remplissez la boîte de dialogue comme ci-dessous.
De nouveau, déroulez la barre des calculs et cliquez à sa droite sur l’icône 
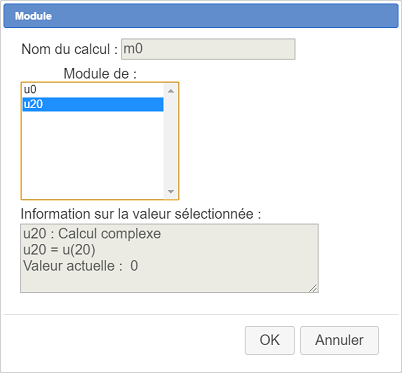
Choisissez dans la liste Module pour créer un calcul nommé m0 qui contiendra le module du complexe u20 comme ci-dessous :
Créons maintenant un calcul réel nommé testm0 qui vaudra 1 si mo est inférieur à 2 et 0 sinon. Pour cela utilisez l’icône  de création d’un calcul réel. Remplissez la boîte de dialogue comme ci-dessous :
de création d’un calcul réel. Remplissez la boîte de dialogue comme ci-dessous :

De nouveau créez un calcul réel nommé test contenant comme formule si(testex,testm0,0). Ainsi, si le calcul u20 existe et si le module de u20 est strictement inférieur à 2, test vaudra 1 et, dans tous les autres cas, test vaudra 0.
A l’aide de l’outil de capture ![]() , amenez le point P assez près de M0 et le point M0 assez proche de P pour que le module de u20 soit strictement inférieur à 2. Appuyez sur la touche F3 ou cliquez sur l’icône
, amenez le point P assez près de M0 et le point M0 assez proche de P pour que le module de u20 soit strictement inférieur à 2. Appuyez sur la touche F3 ou cliquez sur l’icône  pour vérifier que test vaut bien 1.
pour vérifier que test vaut bien 1.
Nous allons maintenant créer un point dont l’affixe sera u0 si test vaut 1 et qui n’existera pas sinon.
Dans la palette de style de points, activez le style "pixel" (tout en bas et à,gauche de la palette de style de point).
Déroulez la barre de création de points et utilisez l’icône  . Dans le champ affixe de la boîte de dialogue, entrez
. Dans le champ affixe de la boîte de dialogue, entrez u0/test et validez.
Mathgraph32 permet de créer des lieux de lieux d’objets.
Créons le lieu d’objet formé de ce dernier point créé généré par les déplacements du point M0 sur le segment auquel il est lié. Pour cela activez l’icône  (sixième rangée d’icônes à partir du bas).
(sixième rangée d’icônes à partir du bas).
Il vous est d’abord demandé de cliquer sur l’objet dont les traces généreront le lieu. Cliquez sur le dernier point créé (il vous sera demandé de préciser le type d’objet : choisissez "Point défini par affixe").
Il vous est ensuite demandé de cliquer sur le point lié clignotant dont les positions généreront le lieu : Cliquez sur le point M0. Demandez un lieu d’objets de 200 valeurs.
Dans la palette de couleurs, activez un gris clair.
Activez à nouveau l’icône  . Cette fois cliquez sur le lieu d’objets que vous venez de créer, puis cliquez sur le point P (point dont les positions généreront le lieu). Demandez un lieu de 50 objets (pour commencer).
. Cette fois cliquez sur le lieu d’objets que vous venez de créer, puis cliquez sur le point P (point dont les positions généreront le lieu). Demandez un lieu de 50 objets (pour commencer).
Nous venons donc de créer un lieu de lieu d’objet !
Capturez les points H et K pour que le lieu d’objet soit calculé sans trop de perte pour des points n’existant pas.
Nous avons donc en gris une approximation de l’ensemble de Julia.
Nous pouvons maintenant augmenter le nombre d’’objets dont est formé le dernier lieu d’objets.
Cliquez dans la barre d’outil supérieure sur l’icône  puis cliquez sur le lieu d’objets gris. Passez maintenant le nombre d’objets à 150 au lieu de 50 et validez.
puis cliquez sur le lieu d’objets gris. Passez maintenant le nombre d’objets à 150 au lieu de 50 et validez.
Un petit calcul : Notre deuxième lieu d’objets est formé de 150 x 200 = 30000 et pour chacun de ces points nous calculons 20 termes complexes d’une suite récurrente, ce qui donne 600 000 calculs complexes !
Utilisez maintenant l’outil  pour masquer les points H, H’, K, K’, P, Q, Q’, M0 et le point créé par son affixe, le segment [QQ’] et le premier lieu d’objets.
pour masquer les points H, H’, K, K’, P, Q, Q’, M0 et le point créé par son affixe, le segment [QQ’] et le premier lieu d’objets.
Nous allons maintenant visualiser la façon dont sont créés les termes successifs de la suite récurrente.
Utilisez l’icône  pour créer un point libre (de préférence à l’intérieur de l’ensemble de Julia).
pour créer un point libre (de préférence à l’intérieur de l’ensemble de Julia).
Utilisez l’icône  pour mesurer son affixe et nommez cette affixe z0.
pour mesurer son affixe et nommez cette affixe z0.
Utilisez l’icône 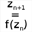 pour créer une nouvelle suite récurrente complexe associée à la fonction f et de premier terme z0 comme indiqué ci-dessous.
pour créer une nouvelle suite récurrente complexe associée à la fonction f et de premier terme z0 comme indiqué ci-dessous.
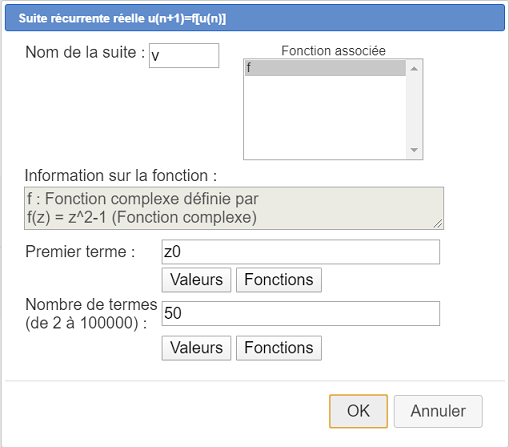
Nous allons maintenant créer le graphe de cette suite. Dans la palette de style de trait, activez le style de point pointillés, et activez la couleur bleue dans la palette de couleurs.
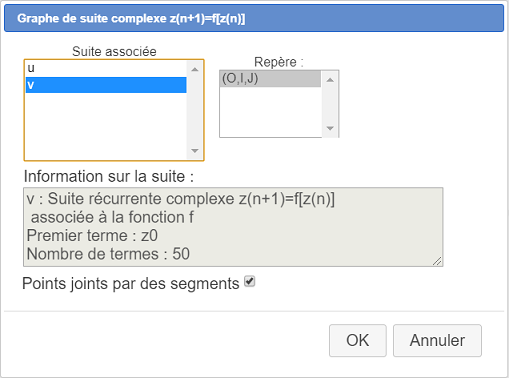
Utilisez l’icône  et remplissez la boîte de dialogue comme ci-dessous. Le graphe de la suite apparaît. Chaque terme est représenté par un point dont il est l’affixe et chaque point est relié au point précédent par un segment.
et remplissez la boîte de dialogue comme ci-dessous. Le graphe de la suite apparaît. Chaque terme est représenté par un point dont il est l’affixe et chaque point est relié au point précédent par un segment.
.
Remarque : Vous pouvez changer le style des points utilisés (ainsi que le style de trait et la couleur) en faisant les choix correspondants dans les palettes de style puis en cliquant sur le graphe après avoir sélectionné l’outil ![]() .
.
Complétons la figure.
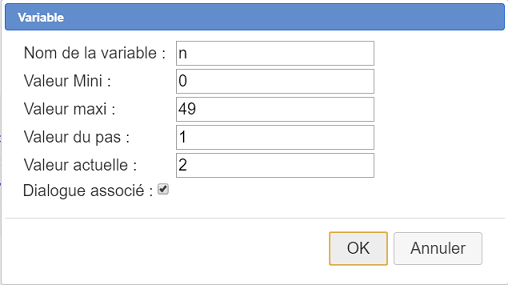
A l’aide de l’icône 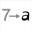 créez une variable nommée n comme indiqué ci-dessous (n’oubliez pas de cocher la case Dialogue associé) :
créez une variable nommée n comme indiqué ci-dessous (n’oubliez pas de cocher la case Dialogue associé) :
Utilisez maintenant l’icône 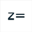 pour créer un calcul complexe nommé zn avec comme formule
pour créer un calcul complexe nommé zn avec comme formule v(n).
Dans la palette de style de point, activez le rond moyen et activez la couleur rouge dans la palette de couleurs.
Créez le point d’affixe zn avec l’icône  .
.
On peut maintenant visualiser le point d’affixe zn en faisant varier n avec les boutons + et - associés à la variable n.
Créons un affichage LaTeX lié à ce dernier point : Activez l’icône  , cliquez sur le dernier point créé et entrez dans le champ Code LaTeX :
, cliquez sur le dernier point créé et entrez dans le champ Code LaTeX : M_{\Val{n}} (vous pouvez utiliser le bouton Insertion de valeur dynamique). Les codes LaTeX \Val sont spécifiques à MathGraph32 et demandent l’affichage d’une valeur. On peut les obtenir avec le bouton Insertion de valeur dynamique).
Déroulez la barre d’outils de calculs et utilisez l’icône pour créez un module de complexe nommé modzn contenant le module du calcul zn.
pour créez un module de complexe nommé modzn contenant le module du calcul zn.
Créons maintenant deux affichages LaTeX libres en haut et à droite de la figure avec l’icône  .
.
Cliquez d’abord sur la figure à l’endroit souhaité.
Dans le premier, entrez le code LaTeX z_{\Val{n}}\approx \Val{zn,3} vous pouvez utiliser le bouton Insertion de valeur dynamique).
Dans le second, entrez le code LaTeX \left| z_{\Val{n}} \right|\approx \Val{modzn,3}.
La figure est terminée.
Si vous voulez obtenir cette figure directement, vous pouvez utiliser l’icône  de la barre supérieure et choisir Figure Par code base 64. Collez alors comme code Base 64 le code ci-dessous puis validez.
de la barre supérieure et choisir Figure Par code base 64. Collez alors comme code Base 64 le code ci-dessous puis validez.
TWF0aEdyYXBoSmF2YTEuMAAAABI+TMzNAAJmcv###wEA#wEAAAAAAAAAAARRAAACpQAAAQEAAAAAAAAAAQAAADH#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAPQ1ZhcmlhYmxlQm9ybmVlAP####8AAW5AHAAAAAAAAAAAAAAAAAAAQEiAAAAAAAA#8AAAAAAAAAEAATAAAjQ5AAEx#####wAAAAEACkNQb2ludEJhc2UA#####wAAAAAADgABTwDAKAAAAAAAAAAAAAAAAAAABQABQHWgAAAAAABAbIzMzMzMzf####8AAAABABRDRHJvaXRlRGlyZWN0aW9uRml4ZQD#####AQAAAAAOAAABAAEAAAACAT#wAAAAAAAA#####wAAAAEAD0NQb2ludExpZURyb2l0ZQD#####AAAAAAAOAAFJAMAYAAAAAAAAAAAAAAAAAAAFAAFAa4mZmZmZmAAAAAP#####AAAAAQAJQ0Ryb2l0ZUFCAP####8AAAAAABAAAAEAAQAAAAIAAAAE#####wAAAAEAFkNEcm9pdGVQZXJwZW5kaWN1bGFpcmUA#####wAAAAAADgAAAQABAAAAAgAAAAX#####AAAAAQAJQ0NlcmNsZU9BAP####8BAAAAAAEAAAACAAAABP####8AAAABABBDSW50RHJvaXRlQ2VyY2xlAP####8AAAAGAAAAB#####8AAAABABBDUG9pbnRMaWVCaXBvaW50AP####8BAAAAAA4AAAEFAAEAAAAIAAAACgD#####AAAAAAAOAAFKAMAoAAAAAAAAwBAAAAAAAAAFAAIAAAAI#####wAAAAIAB0NSZXBlcmUA#####wDm5uYAAQAAAAIAAAAEAAAACgAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAE#8AAAAAAAAAAAAAE#8AAAAAAAAP####8AAAABAApDVW5pdGV4UmVwAP####8ABHVuaXQAAAAL#####wAAAAEAC0NIb21vdGhldGllAP####8AAAAC#####wAAAAEACkNPcGVyYXRpb24DAAAAAT#wAAAAAAAA#####wAAAAEAD0NSZXN1bHRhdFZhbGV1cgAAAAz#####AAAAAQALQ1BvaW50SW1hZ2UA#####wEAAAAAEAACVyIBAQAAAAAEAAAADf####8AAAABAAlDTG9uZ3VldXIA#####wAAAAIAAAAOAAAABQD#####AQAAAAAQAAFIAAAAAAAAAAAAQAgAAAAAAAAFAAE#+uTsl#8SBAAAAAUAAAAFAP####8BAAAAABAAAUsAAAAAAAAAAABACAAAAAAAAAUAAb#ryZ2wv4GUAAAABv####8AAAABABFDU3ltZXRyaWVDZW50cmFsZQD#####AAAAAgAAABAA#####wEAAP8AEAACSCcAAAAAAAAAAABACAAAAAAAAAUAAAAAEAAAABIAAAAQAP####8BAAD#ABAAAksnAAAAAAAAAAAAQAgAAAAAAAAFAAAAABEAAAAS#####wAAAAEACENTZWdtZW50AP####8BAAD#ABAAAAEAAQAAABEAAAAUAAAABQD#####AAAA#wAQAAFQAAAAAAAAAAAAQAgAAAAAAAAFAAE#1pePbVhugAAAABX#####AAAAAQAMQ1RyYW5zbGF0aW9uAP####8AAAACAAAAFgAAABAA#####wEAAP8AEAABUQAAAAAAAAAAAEAIAAAAAAAABQAAAAAQAAAAFwAAABAA#####wEAAP8AEAACUScAAAAAAAAAAABACAAAAAAAAAUAAAAAEwAAABcAAAATAP####8BAAD#ABAAAAEAAQAAABgAAAAZAAAABQD#####Af8AAAAQAAJNMAAAAAAAAAAAAEAIAAAAAAAABQABP97ZVufxPg0AAAAa#####wAAAAIADUNNZXN1cmVBZmZpeGUA#####wACdTAAAAALAAAAG#####8AAAABAA1DRm9uY0NvbXBsZXhlAP####8AAWYABXpeMi0xAAAADgH#####AAAAAQAKQ1B1aXNzYW5jZf####8AAAACABFDVmFyaWFibGVGb3JtZWxsZQAAAAAAAAABQAAAAAAAAAAAAAABP#AAAAAAAAAAAXr#####AAAAAQARQ1N1aXRlUmVjQ29tcGxleGUA#####wABdQAAAAFANQAAAAAAAP####8AAAABABdDUmVzdWx0YXRWYWxldXJDb21wbGV4ZQAAABwAAAAd#####wAAAAEAD0NDYWxjdWxDb21wbGV4ZQD#####AAN1MjAABXUoMjAp#####wAAAAEAFkNBcHBlbEZvbmN0aW9uQ29tcGxleGUAAAAeAAAAAUA0AAAAAAAA#####wAAAAEADkNUZXN0RXhpc3RlbmNlAP####8ABnRlc3RleAAAAB######AAAAAQAHQ01vZHVsZQD#####AAJtMAAAAB######AAAAAQAHQ0NhbGN1bAD#####AAZ0ZXN0bTAABG0wPDIAAAAOBAAAAA8AAAAhAAAAAUAAAAAAAAAAAAAAHwD#####AAR0ZXN0ABNzaSh0ZXN0ZXgsdGVzdG0wLDAp#####wAAAAEADUNGb25jdGlvbjNWYXIAAAAADwAAACAAAAAPAAAAIgAAAAEAAAAAAAAAAP####8AAAABAA9DUG9pbnRQYXJBZmZpeGUA#####wH#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAFAAAAAAsAAAAOAwAAABoAAAAcAAAAGgAAACP#####AAAAAgASQ0xpZXVPYmpldFBhclB0TGllAP####8BAH8AAAAAJAAAAAFAYsAAAAAAAAAAABsAAAAJAAAAGwAAABwAAAAeAAAAHwAAACAAAAAhAAAAIgAAACMAAAAkAAAAIgD#####APLy8gAAACUAAAABQGkAAAAAAAAAAAAWAAAADwAAABYAAAAXAAAAGAAAABkAAAAaAAAAGwAAABwAAAAeAAAAHwAAACAAAAAhAAAAIgAAACMAAAAkAAAAJQAAAAMA#####wAAAAAAEAABTQAAAAAAAAAAAEAIAAAAAAAABQABQHggAAAAAABAYkzMzMzMzQAAABUA#####wACejAAAAALAAAAJwAAABkA#####wABdgAAAAFASQAAAAAAAAAAABoAAAAoAAAAHf####8AAAABABdDR3JhcGhlU3VpdGVSZWNDb21wbGV4ZQD#####AAAA#wEBAAAAKQAAAAsBBQAAABsA#####wACem4ABHYobikAAAAcAAAAKQAAABoAAAABAAAAIQD#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAUAAAAACwAAABoAAAAr#####wAAAAIABkNMYXRleAD#####AP8AAAEAAAAsEAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAC01fe1xWYWx7bn19AAAAHgD#####AAVtb2R6bgAAACsAAAAkAP####8A#wAAAf####8SQDUAAAAAAABAO2ZmZmZmZgAAAAAAAAAAAAAAAAABAAAAAAAAAAAAHXpfe1xWYWx7bn19XGFwcHJveCBcVmFse3puLDN9AAAAJAD#####AP8AAAH#####EEAyAAAAAAAAQE8zMzMzMzQAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAC9cbGVmdHwgel97XFZhbHtufX0gXHJpZ2h0fFxhcHByb3ggXFZhbHttb2R6biwzfQAAAA###########w==