Toutes les versions de cet article : [English] [Español] [français]
En este artículo vamos a mostrar cómo ilustrar el TP4 del libro de Terminale S publicado por Magnard (el primer libro de TS bajo licencia libre), la asociación Sesamath está a cargo del manual numérico. Cliquear sobre : este vínculo para leer el texto de este TP.
Se trata entonces, de visualizar el conjunto de los puntos de afijo z0 tales que la sucesión recurrente definida por $z_{n+1}=z_n^2-1$ sea acotada y de visualizar el comportamiento de dicha sucesión según su primer término.
A continuación se ve la figura que se quiere obtener, animada por el motor JavaScript de MathGraph32. Se puede capturar el punto M y cliquear sobre los botones + y - para visualizar los primeros 50 términos de la sucesión.
Para esta figura, es preferible utilizar la versión 5.1 de MathGraph32 (o una versión posterior) porque esta versión permite los lugares de objetos con un mayor número de objetos.
Para empezar, recordemos algunos puntos de la nueva ergonomía de MathGraph32. Los íconos están ahora agrupados por tipo.
De arriba a abajo :
– Íconos de creación de puntos.
– Íconos de creación de rectas.
– Íconos de creación de segmentos, semirrectas, vectores.
– Íconos de creación de circunferencias y arcos de circunferencias.
– Íconos de creación de polígonos.
– Íconos de creación de marcas (de segmentos y de ángulos).
– Íconos de creación de lugares de puntos, curvas, lugares de objetos.
– Íconos de creación de transformaciones.
– Íconos de medidas.
– Íconos de creación de visualizaciones.
– Íconos de creación de cálculos.
– Íconos de creación de superficies.
Comencemos por crear una nueva figura dotada de un referencial ortonormal con la ayuda del ícono ![]() . Elijamos un referencial ortonormal no cuadriculado y sin graduaciones.
. Elijamos un referencial ortonormal no cuadriculado y sin graduaciones.
Con la ayuda de la herramienta de captura ![]() alejemos el punto I del punto O como en la figura anterior.
alejemos el punto I del punto O como en la figura anterior.
Con la ayuda del ícono ![]() de creación de punto ligado, creemos un punto H ligado al eje de las abscisas (a la derecha de I) y un punto K ligado al eje de las ordenadas (un poco por debajo de J).
de creación de punto ligado, creemos un punto H ligado al eje de las abscisas (a la derecha de I) y un punto K ligado al eje de las ordenadas (un poco por debajo de J).
En la paleta de colores, activamos el color azul.
Con la herramienta ![]() , creemos las imágenes H’ y K’ de H y de K en la simetría central de centro O (cliquear en primer lugar sobre el punto O, centro de la simetría, a continuación sobre los puntos H y K).
, creemos las imágenes H’ y K’ de H y de K en la simetría central de centro O (cliquear en primer lugar sobre el punto O, centro de la simetría, a continuación sobre los puntos H y K).
Utilicemos el ícono ![]() para unir los puntos K y K’ por un segmento.
para unir los puntos K y K’ por un segmento.
Con la herramienta ![]() creemos un punto ligado al segmento [KK’], lo nominaremos P.
creemos un punto ligado al segmento [KK’], lo nominaremos P.
Utilicemos ahora la herramienta ![]() para crear las imágenes Q y Q’ de los puntos H y H’ por la traslación de vector $\overrightarrow{OP}$ (para ello cliquear en primer lugar sobre los puntos O y P luego sobre los puntos H y H’).
para crear las imágenes Q y Q’ de los puntos H y H’ por la traslación de vector $\overrightarrow{OP}$ (para ello cliquear en primer lugar sobre los puntos O y P luego sobre los puntos H y H’).
Unamos los puntos Q y Q’ mediante un segmento (ícono ![]() ).
).
En la paleta de colores, activamos el color rojo y, con el ícono ![]() , creemos un punto ligado al segmento [QQ’] que llamaremos M0.
, creemos un punto ligado al segmento [QQ’] que llamaremos M0.
Ahora le demandamos al software medir el afijo del punto M0 en el referencial (O, I, J). Para ello, utilizamos el ícono ![]() y cliqueamos sobre el punto M0. Se abre un cuadro de diálogo. Introducimos : u0 como nombre de este afijo y validamos.
y cliqueamos sobre el punto M0. Se abre un cuadro de diálogo. Introducimos : u0 como nombre de este afijo y validamos.
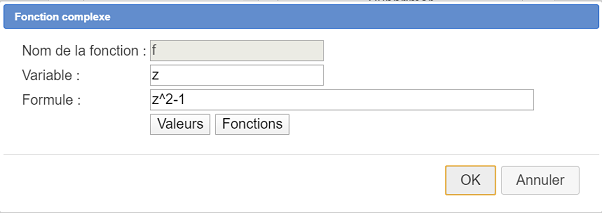
Para crear una sucesión recurrente compleja debemos crear primero una función compleja de una variable compleja. Utilizamos para ello el ícono ![]() (que se encuentra entre los íconos de cálculo, cuarta fila de íconos de la parte inferior) y completamos el cuadro de diálogo como se muestra a continuación.
(que se encuentra entre los íconos de cálculo, cuarta fila de íconos de la parte inferior) y completamos el cuadro de diálogo como se muestra a continuación.
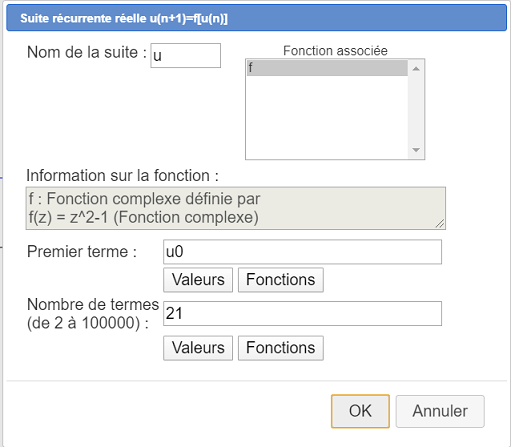
Para crear una sucesión recurrente, utilizamos el ícono ![]() (la misma fila de íconos que la precedente) y completamos el cuadro de diálogo como se muestra a continuación :
(la misma fila de íconos que la precedente) y completamos el cuadro de diálogo como se muestra a continuación :
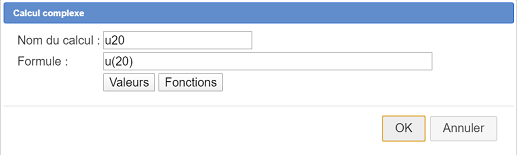
Utilizamos ahora el ícono ![]() para crear un cálculo complejo llamado u20 con la fórmula
para crear un cálculo complejo llamado u20 con la fórmula u(20) como se muestra seguidamente.
Nota : Puede ser que el software nos advierta de que no existe ese cálculo (por razones de desbordamiento de la capacidad de cálculo). Si este es el caso, aceptamos y aproximamos más el punto M0 al punto P y el punto P al punto O. A continuación comprobamos con la tecla de función F6 que el cálculo u20 existe.
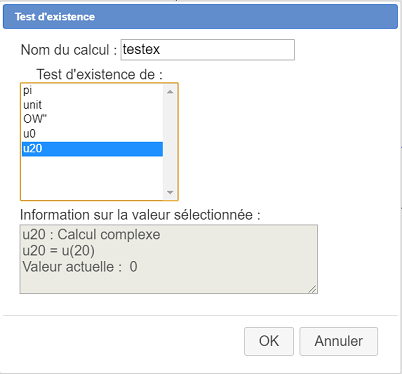
Utilizamos ahora el menú Cálculos - Nuevo cálculo en R - Test de existencia de un valor para crear un test de existencia del valor de u20 : Si ese cálculo existe, u20 valdrá 1 y si no valdrá 0. Completamos la caja de diálogo se ve a continuación.
A continuación, utilizamos el menú Cálculos - Nuevo cálculo en R - Módulo de complejo para crear un cálculo de nombre mo que contiene al módulo del complejo u20 de la siguiente manera :
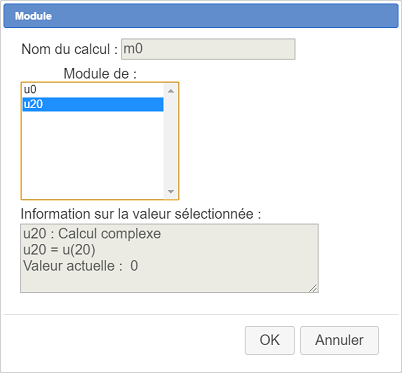
Vamos a crear ahora un cálculo con nombre testmo que tendrá el valor 1 si mo es inferior a 2 y 0 en caso contrario. Para ello, utilizamos el ícono ![]() de creación de un cálculo real. Completando el cuadro de diálogo como se muestra a continuación :
de creación de un cálculo real. Completando el cuadro de diálogo como se muestra a continuación :

Nuevamente creamos un cálculo real con nombre test conteniendo como fórmula si(testex,testmo,0). Así, si el cálculo u20 existe y si el módulo de u20 es estrictamente inferior a 2, test valdrá 1 y, en todos los otros casos, test valdrá 0.
Usando la herramienta de captura ![]() , movamos el punto P lo suficientemente cerca de M0 y el punto M0 estará lo suficientemente cerca de P para que el módulo de u20 sea estrictamente menor que 2. Pulsamos la tecla F6 para verificar que test vale 1.
, movamos el punto P lo suficientemente cerca de M0 y el punto M0 estará lo suficientemente cerca de P para que el módulo de u20 sea estrictamente menor que 2. Pulsamos la tecla F6 para verificar que test vale 1.
Ahora vamos a crear un punto cuyo afijo será u0 si test vale 1 y que no existe de otra manera. En la paleta Estilo de puntos, seleccione el estilo "pixel" (en la parte inferior y al centro de la paleta). Utilicemos el ícono ![]() . En el campo afijo, del cuadro de diálogo, introducimos
. En el campo afijo, del cuadro de diálogo, introducimos u0/test y validamos (test debe ser igual a 1 para que la creación sea aceptada).
Creamos el lugar de objeto formado por este último punto creado generado por el desplazamiento del punto M0 sobre el segmento aquel al que está ligado. Para esto activamos el ícono ![]() (sexta fila de íconos de la parte inferior).
(sexta fila de íconos de la parte inferior).
Ante todo se nos pide cliquear sobre el objeto cuyas trazas generarán el lugar. Cliqueamos sobre el último punto creado (se nos pedirá precisar el tipo de objeto : elegimos "Punto definido por abscisa").
Seguidamente se nos pide cliquear sobre el punto ligado parpadeante cuyas posiciones generarán el lugar : Cliqueamos sobre el punto M0. Consideramos un lugar de objetos de 200 valores.
MathGraph32 puede crear lugares de lugares de objetos.
En la paleta de colores, activamos un color gris claro.
Activamos nuevamente el ícono ![]() . Esta vez cliqueamos sobre el lugar de objetos que venimos de crear, luego cliqueamos sobre el punto P (punto cuyas trazas generarán el lugar). Consideramos un lugar de 150 objetos.
. Esta vez cliqueamos sobre el lugar de objetos que venimos de crear, luego cliqueamos sobre el punto P (punto cuyas trazas generarán el lugar). Consideramos un lugar de 150 objetos.
Capturamos los puntos H y K para que el lugar de objetos sea calculado sin demasiada pérdida de puntos no existentes.
Tenemos entonces en gris una aproximación al conjunto de Julia.
Utilizamos la herramienta ![]() para ocultar los puntos H, H’, K, K’, P, Q, Q’, M0 y el punto creado por su afijo, el segmento [QQ’] y el primer lugar de objetos.
para ocultar los puntos H, H’, K, K’, P, Q, Q’, M0 y el punto creado por su afijo, el segmento [QQ’] y el primer lugar de objetos.
Ahora vamos a ver cómo se crean los términos sucesivos de la sucesión recurrente.
Utilizamos el ícono ![]() para crear un punto libre (de preferencia en el interior del conjunto de Julia).
para crear un punto libre (de preferencia en el interior del conjunto de Julia).
Utilizamos el ícono ![]() para medir su afijo y nominamos ese afijo z0.
para medir su afijo y nominamos ese afijo z0.
Utilizamos el ícono ![]() para crear una nueva sucesión recurrente compleja asociada a la función f y de primer término z0 como se indica a continuación.
para crear una nueva sucesión recurrente compleja asociada a la función f y de primer término z0 como se indica a continuación.
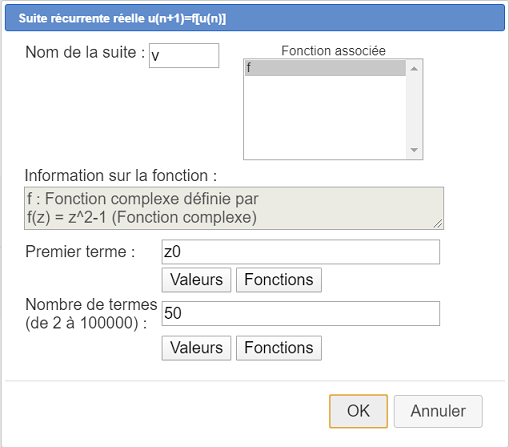
Ahora vamos a crear la gráfica de esta sucesión. En la paleta de estilo de trazo, hacemos clic en el estilo punteado, y activamos el color azul en la paleta de colores.
Utilizamos el ícono ![]() y completamos el cuadro de diálogo como se muestra a continuación. Aparece el gráfico de la sucesión. Cada término está representado por un punto que es el afijo y cada punto está conectado con el punto precedente por un segmento.
y completamos el cuadro de diálogo como se muestra a continuación. Aparece el gráfico de la sucesión. Cada término está representado por un punto que es el afijo y cada punto está conectado con el punto precedente por un segmento.
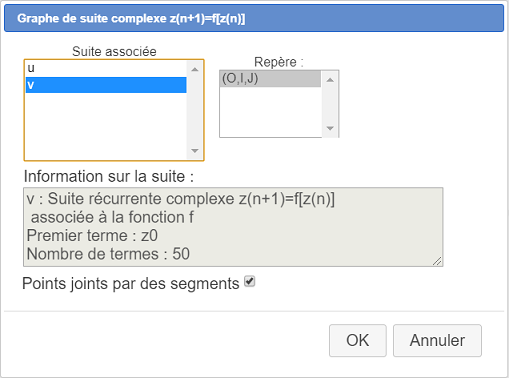
.
Nota : Podemos cambiar el estilo de los puntos utilizados (y el estilo de trazo y el color) efectuando las elecciones correspondientes en las paletas de estilo y haciendo luego clic sobre la gráfica después de haber seleccionado la herramienta ![]() .
.
Completemos la figura.
Con la ayuda del ícono ![]() creamos una variable nominada n como se indica abajo (no olvidar de marcar la casilla Diálogo asociado :
creamos una variable nominada n como se indica abajo (no olvidar de marcar la casilla Diálogo asociado :
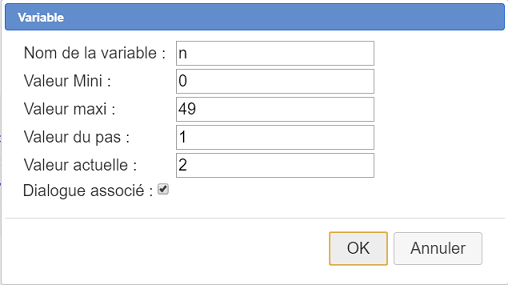
Utilizamos ahora el ícono ![]() para crear un cálculo nominado zn con la fórmula
para crear un cálculo nominado zn con la fórmula z(n).
En la paleta de estilo de punto, activamos el tamaño medio y activamos el color rojo en la paleta de colores.
Creamos el punto de afijo zn con el ícono ![]() .
.
Ahora podemos ver el punto de afijo zn haciendo variar n con los signos + y - asociados a la variable n.
Creamos una visualización LaTeX ligada a este último punto : Activamos el ícono ![]() , Cliqueamos sobre el último punto creado y entramos en el campo Code LaTeX :
, Cliqueamos sobre el último punto creado y entramos en el campo Code LaTeX : M_{\Val{n}} (podemos utilizar el botón Inserción de valor dinámico). Los códigos LaTeX \Val son específicos de MathGraph32 y requieren la visualización de un valor. Se pueden obtener con el botón Inserción de valor dinámico.
Utilizamos el menú Cálculos- Nuevo cálculo en R - Módulo de complejo et creamos un cálculo nominado modzn conteniendo el módulo del cálculo zn.
Creamos dos visualizaciones LaTeX libres en la parte superior derecha de la figura con el ícono ![]() .
.
En primer lugar, hacemos clic sobre la figura en la ubicación deseada.
En la primera, entramos el código LaTeX z_{\Val{n}}\approx \Val{zn,3} podemos utilizar el botón Inserción de valor dinámico.
En la segunda, entramos el código LaTeX \left| z_{\Val{n}} \right|\approx \Val{modzn,3}.
La figura está terminada.