Toutes les versions de cet article : [Español] [français]
Se trata aquí de representar gráficamente la sucesión recurrente compleja definida por $\begin{array}{l}x_{n+1}=by_n+f\left( x_n \right)\\ y_{n+1}=-x_n+f\left(x_{n+1}\right)\end{array}$.
La función f está definida por $f(x)=ax+\frac{2(1-a)x^2}{1+x^2}$. Daremos al usuario la posibilidad de modificar los valores de a, b así como la fórmula que la define f.
Para lograr esta figura debemos utilizar la versión 5.1 o posterior de MathGraph32 (porque es sólo a partir de esta versión que las sucesiones recurrentes pueden tener hasta 100000 términos).
Aquí debajo está la figura a realizar, animada por el motor JavaScript vectorial de MathGraph32 :
JavaScript es más lento que Java, se necesita un tiempo antes de que la figura reaccione a los cambios (hay 50000 términos de una sucesión compleja a calcular cada vez).
Veamos cómo lograr esta figura con la versión 5.1 de MathGraph32.
Comencemos por utilizar el ícono ![]() para crear una nueva figura munida de un referencial ortonormal, con punteado y graduaciones.
para crear una nueva figura munida de un referencial ortonormal, con punteado y graduaciones.
En primer lugar crearemos una nueva variable que nos permitirá acercar y alejar la figura.
Utilizamos el ícono ![]() (que como todos los íconos de creación de cálculo que está en la penúltima fila de íconos) y completamos el cuadro de diálogo como se muestra a continuación (no olvidemos tildar la casilla Diálogo asociado) :
(que como todos los íconos de creación de cálculo que está en la penúltima fila de íconos) y completamos el cuadro de diálogo como se muestra a continuación (no olvidemos tildar la casilla Diálogo asociado) :
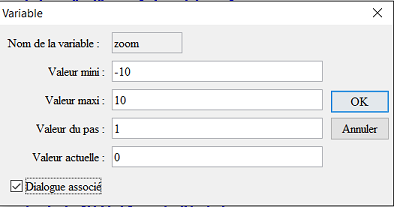
Las variables siempre se añaden al comienzo de la lista de los objetos creados. Así podremos cambiar nuestro referencial mediante el uso de la variable zoom.
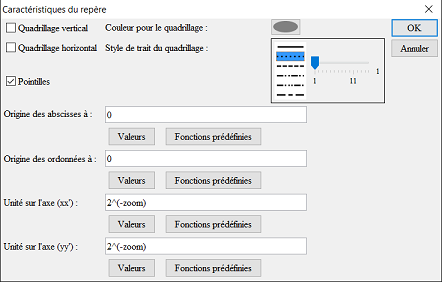
Utilizamos el menú Modificar - Referencial, elegimos el referencial (O, I, J) y completamos la caja de diálogo como se ve seguidamente (ingresamos 2^(-zoom) como unidad sobre los dos ejes) :
Nuevamente utilizamos el ícono ![]() para crear una variable n que contendrá el número de términos de la sucesión :
para crear una variable n que contendrá el número de términos de la sucesión :
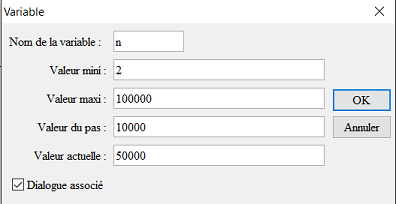
Atención : Para una máquina potente, tal vez es mejor entrar un valor actual de n igual a 20000.
Utilicemos el ícono ![]() para crear dos cálculos reales :
para crear dos cálculos reales :
– El primer cálculo nominado a contiene como fórmula 0.7185
– El segundo cálculo nominado b contiene como fórmula 0.9997
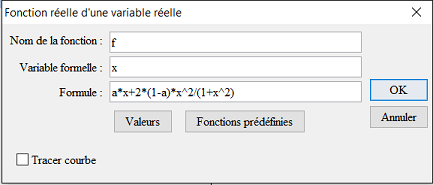
Ahora creamos la función real f definida por f(x)=a*x+2*(1-a)*x^2/(1+x^2) con el ícono ![]() (no olvidemos destildar la casilla Trazar curva) :
(no olvidemos destildar la casilla Trazar curva) :
Creamos un cálculo complejo llamado z0 con el ícono ![]() . Este cálculo contendrá el primer término de la sucesión. Entramos como fórmula
. Este cálculo contendrá el primer término de la sucesión. Entramos como fórmula -6-6*i.
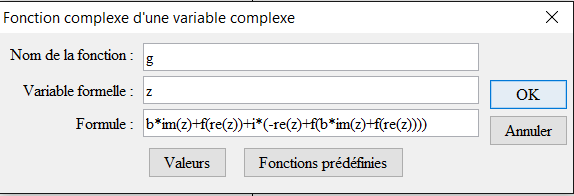
Ahora debemos crear la función compleja de una variable compleja g que va a definir la sucesión recurrente compleja. Utilizamos el ícono ![]() y completamos la fórmula como se muestra a continuación, siendo la fórmula a introducir
y completamos la fórmula como se muestra a continuación, siendo la fórmula a introducir b*im(z)+f(re(z))+i*(-re(z)+f(b*im(z)+f(re(z)))).
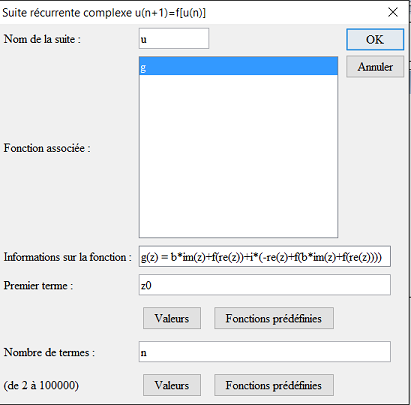
Ahora podemos definir la sucesión recurrente compleja con el ícono ![]() de la siguiente manera :
de la siguiente manera :
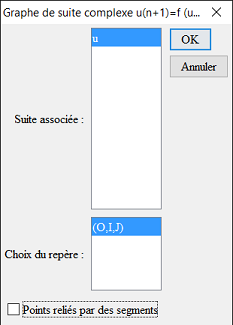
Y ahora vamos a crear la gráfica de esta sucesión con el ícono ![]() . Activando previamente el color azul en la paleta de colores y el estilo de punto "pixel" que existe desde la versión 5.1 y se encuentra en la parte inferior de la paleta de estilo de punto. Completamos el cuadro de diálogo como se muestra a continuación teniendo en cuenta desmarcar la casilla Puntos conectados por segmentos :
. Activando previamente el color azul en la paleta de colores y el estilo de punto "pixel" que existe desde la versión 5.1 y se encuentra en la parte inferior de la paleta de estilo de punto. Completamos el cuadro de diálogo como se muestra a continuación teniendo en cuenta desmarcar la casilla Puntos conectados por segmentos :
Ahora vamos a darle al usuario la capacidad de modificar sobre la figura los valores de a, b y la fórmula f.
En la paleta de colores, activamos el color marrón.
Activamos la herramienta ![]() de creación de un editor de fórmula (que se encuentra en la tercera fila de iconos de la parte inferior) y cliqueamos en la parte superior izquierda de la figura. Completamos el cuadro de diálogo como se muestra a continuación :
de creación de un editor de fórmula (que se encuentra en la tercera fila de iconos de la parte inferior) y cliqueamos en la parte superior izquierda de la figura. Completamos el cuadro de diálogo como se muestra a continuación :
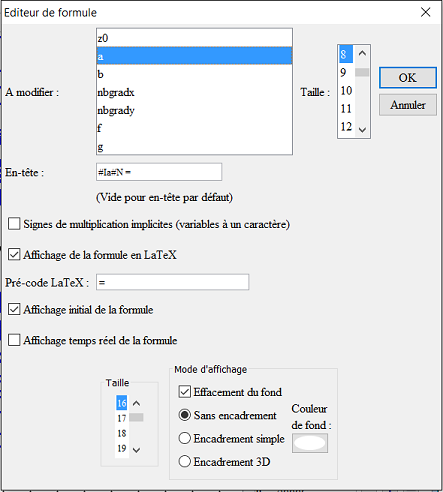
Los caracteres $ enmarcan el encabezamiento utilizado para el estilo de visualización de LaTeX.
Del mismo modo creamos en el editor de fórmulas para modificar las fórmulas del cálculo b, del cálculo complejo z0 (primer término de la sucesión) y de la función f. Para el editor asociado a z0 podemos desmarcar la casilla Signos de multiplicación implícitos lo que permite por ejemplo, ingresar como fórmula 6+6i en lugar de 6+ 6*i.
La figura está terminada. Podemos acercar o alejar la figura con los botones + y - de la variable zoom, cambiar el número de términos de la sucesión, los valores a, b, z0 y la fórmula de la función f.
Ensayemos por ejemplo con los valores siguientes :
– a = -0.77, b=0.95, z0=3+i, n = 50000
– a=0.31, b=1, z0=12, n = 50000 (dézoomer)
– a =-0.05, b=0.999,z°=4-4*i, n = 50000
– a=6, b=0.9996, z0=5 et f(x)=a*x+2*(1-a)*x^2/(1+4*x^2), n = 50000
- a = -0.1793, b = 1, f(x) = abs(a*x-arctan(a-x)), n = 60000, zoom = -1
- a = 0.544, b = 1, f(x) = a*x+arctan(abs(x-a)), n = 100000, zoom = -1
- a = 0.223542555, b = 1, f(x) = a*x+arctan(x^3/(1+a*x^3)), n = 90000, zoom = -2
- a = -0.9640736808, b = 0.9644999159, f(x) = a*x-abs(arctan(a-x)+b*x^2/(1+x^2)), n = 60000, zoom = 2
- a = 0.733303464, b = 1, abs(a*x-(b*x^2-sin(a))/(a*x^2+cos(b)^2)), n = 40000, zoom = -6
- a = 0.09798342, b = 1, f(x) = a*x+(3-a)/(a+exp(x)), n = 80000, zoom = -5
Una observación final : Para estos valores :
– A = 0,403, b = 1, f (x) = a * xx / (a + x) + arctan (a * x), n = 100000, zoom = -4, la figura obtenida en esta página HTML no es el misma que la obtenida con el software en Java. Puede ser diferente según los navegadores.
Después de la exploración, parece que ínfimas diferencias en el cálculo de la función arcotangente en Java y JavaScript producen sucesiones que proporcionan un cierto número de términos de divergencias importantes. A partir del índice 148 aparecerán decimales diferentes en los tres últimos dígitos sobre 12 y luego se acumulan las diferencias.