Toutes les versions de cet article : [Español] [français]
Este artículo ha sido revisado y adaptado a la versión Javascript de MathGraph32. Debe utilizar la versión 7.3.5 o posterior.
En este artículo explicaremos cómo usar las construcciones recursivamente para obtener una versión simplificada de la figura a continuación.
Una figura viable completa está disponible aquí :
Para hacer esto, crearemos dos construcciones que implementaremos recursivamente.
Nota preliminar : Si no pudo crear sus construcciones (pasos 1 y 3), puede descargarlas a continuación, descomprimirlas en una carpeta en su disco duro y usar esos archivos en lugar de los que se supone que debe tener creado por su cuenta
Cree una figura en blanco (con longitud unidad) con el icono  .
.
Asegúrrese con el ícono  que la unidad de ángulo de la figura es el grado.
que la unidad de ángulo de la figura es el grado.
Usando el ícono  (creación de un cálculo real), cree seis cálculos (en este orden) :
(creación de un cálculo real), cree seis cálculos (en este orden) :
– Un cálculo llamado coefRay con la fórmula 0.7
– Un cálculo llamado coefAng con la fórmula 0.7
– Un cálculo llamado p con la fórmula 0.25
– Un cálculo denominado nbsDem con la fórmula 1
– Un cálculo llamado n con la fórmula 0
– Un cálculo llamado ray con la fórmula 4.8
– Un cálculo llamado ang con la fórmula 45
Cree un punto libre al que llamaremos A con el icono  . Colóquelo a la izquierda y en el centro de la figura.
. Colóquelo a la izquierda y en el centro de la figura.
Con el icono  cree una recta horizontal que pase por A.
cree una recta horizontal que pase por A.
Use el icono  para crear la circunferencia de centro A y radio ray.
para crear la circunferencia de centro A y radio ray.
Utilice el icono  para crear la intersección de la recta horizontal con esta circunferencia (haga clic cuando vea que se muestra esta intersección).
para crear la intersección de la recta horizontal con esta circunferencia (haga clic cuando vea que se muestra esta intersección).
Use la herramienta rotación  para crear la imagen B del último punto creado por la rotación del centro A y el ángulo ang (primero haga clic en el centro A de la rotación, ingrese ang como el ángulo y luego haga clic sobre el último punto creado).
para crear la imagen B del último punto creado por la rotación del centro A y el ángulo ang (primero haga clic en el centro A de la rotación, ingrese ang como el ángulo y luego haga clic sobre el último punto creado).
Utilice la herramienta simetría axial  para crear la imagen C del punto B en la simetría axial con respecto a la recta horizontal (debe hacer clic primero en el eje de simetría y luego en el punto del que queremos crear la imagen).
para crear la imagen C del punto B en la simetría axial con respecto a la recta horizontal (debe hacer clic primero en el eje de simetría y luego en el punto del que queremos crear la imagen).
Ahora cree una recta horizontal que pase por B (icono  ).
).
Ahora cree, en este orden, cuatro cálculos reales ( ) :
) :
– Un cálculo llamado q con la fórmula 1-p
– Un cálculo llamado n1 con la fórmula n+1
– Un cálculo llamado ray1 con la fórmula ray*coefRay
– Un cálculo llamado ang1 con la fórmula ang*coefAng
Ahora use el ícono  para crear un punto D ligado a la recta horizontal que pasa por B (como se muestra a continuación).
para crear un punto D ligado a la recta horizontal que pasa por B (como se muestra a continuación).
Cree en este orden, tres cálculos reales ( ) :
) :
– Un cálculo llamado n2 con la fórmula n+1
– Un cálculo llamado ray2 con la fórmula ray*coefRay
– Un cálculo llamado ang2 con la fórmula ang*coefAng
Utilice la herramienta simetría axial  para crear la imagen E del punto D en la simetría axial con respecto a la recta horizontal que pasa por A.
para crear la imagen E del punto D en la simetría axial con respecto a la recta horizontal que pasa por A.
En la Paleta de estilo de flecha, active la flecha sólida pequeña.
Utilice el icono  para crear los vectores $\overrightarrow{AB}$ y $\overrightarrow{AC}$ .
para crear los vectores $\overrightarrow{AB}$ y $\overrightarrow{AC}$ .
Con el icono  cree los puntos medios de los segmentos [AB] y [AC].
cree los puntos medios de los segmentos [AB] y [AC].
Ahora cree en azul una visualización del valor de p ligado al punto medio del segmento [AB]. Para hacer esto, use el ícono  , haga clic en el centro y luego complete el cuadro de diálogo como se muestra a continuación (se solicitan 3 decimales y una pantalla centrada horizontal y verticalmente) :
, haga clic en el centro y luego complete el cuadro de diálogo como se muestra a continuación (se solicitan 3 decimales y una pantalla centrada horizontal y verticalmente) :
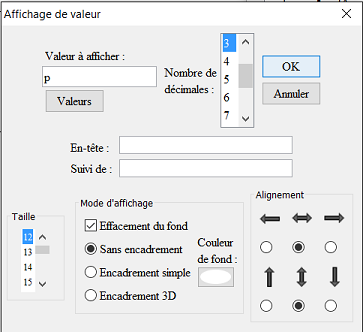
Del mismo modo, cree en verde, una visualización del valor de q ligado al punto medio de [AC] :
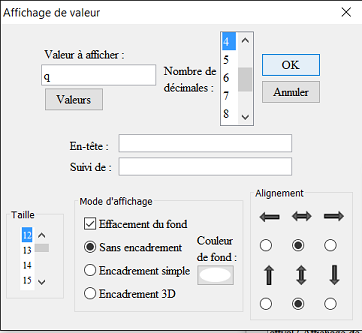
Ahora cree los puntos medios de los segmentos [BD] y [CE] (icono  ).
).
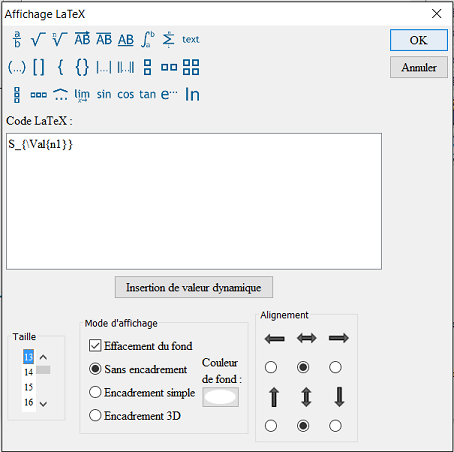
Ahora crearemos en azul una visualización LaTeX ligada al punto medio de [BD] con el icono  . Para hacer esto, haga clic en el punto medio de [BD] y luego complete el cuadro de diálogo como se muestra a continuación. El código LaTeX es
. Para hacer esto, haga clic en el punto medio de [BD] y luego complete el cuadro de diálogo como se muestra a continuación. El código LaTeX es S_{\Val{n1}}. \Val{n1} es un código LaTeX específico de MathGraph32 que solicita una visualización dinámica del valor de n1 (con dos decimales por defecto, lo cual no importa aquí porque n1 es un número entero ). Obtendremos así la letra S con el valor de n1 como índice :
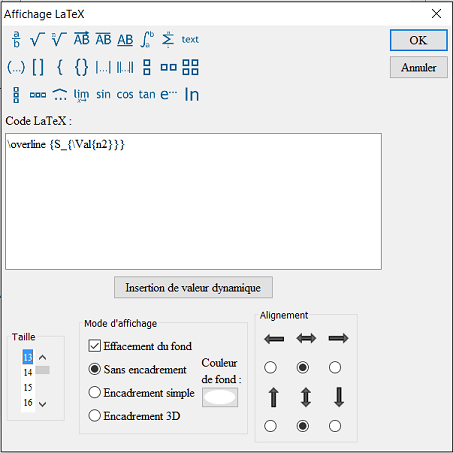
De manera similar, cree en verde una visualización LaTeX ligada al punto medio de [CE] como se muestra a continuación. El código LaTeX es \overline {S_{\Val{n2}}}. Mostrará, debajo de una barra, la letra S con el valor de n2 como índice :
Nuestra figura está lista para crear nuestra primera construcción.
Es importante que los objetos hayan sido creados en el orden que hemos indicado. Si el orden es incorrecto, la macro no se puede implementar de forma iterativa. Puede modificar este orden utilizando el protocolo de la figura (icono  de la barra de herramientas superior). En este cuadro de diálogo, las flechas de la derecha le permiten subir o bajar un objeto en la lista de objetos creados.
de la barra de herramientas superior). En este cuadro de diálogo, las flechas de la derecha le permiten subir o bajar un objeto en la lista de objetos creados.
Use la herramienta  para ocultar los puntos medios de [BD] y [CE].
para ocultar los puntos medios de [BD] y [CE].
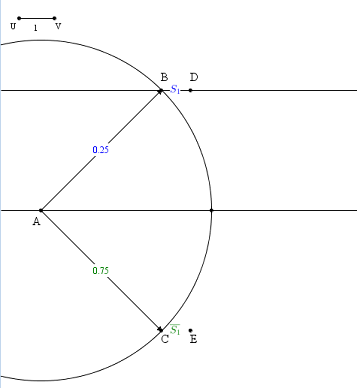
En esta etapa, su figura debe parecerse a la siguiente figura :
Pasemos a crear la construcción. Para gestionar las construcciones utilice el icono  que muestra iconos suplementarios.
que muestra iconos suplementarios.
Haga clic en el icono  (creación de una construcción) y luego elija el elemento Elección de objetos fuentes numéricos.
(creación de una construcción) y luego elija el elemento Elección de objetos fuentes numéricos.
Al principio, obtiene el cuadro de diálogo a continuación (el orden de los elementos a la izquierda debe ser el mismo) :
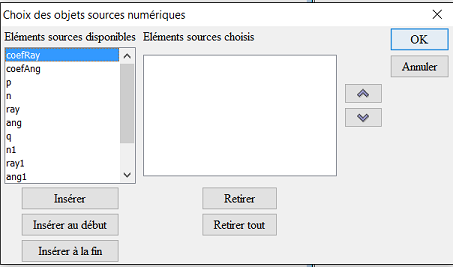
Haga clic en el botón Insertar (o haga doble clic en cada valor) para obtener esto :
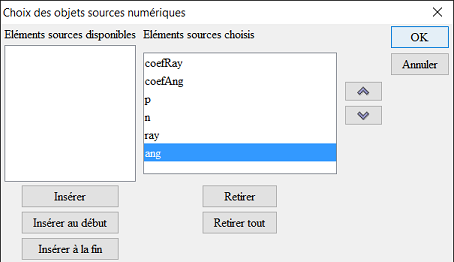
Designemos ahora los objetos fuentes gráficos : Sólo hay uno : el punto A.
Utilice de nuevo el icono  , elija el elemento Elección de objetos fuentes gráficos y luego haga clic en el punto A que comienza a parpadear.
, elija el elemento Elección de objetos fuentes gráficos y luego haga clic en el punto A que comienza a parpadear.
En la parte inferior derecha de la ventana, haga clic en el icono rojo STOP para indicar que se han designado todos los objetos de origen gráfico.
Designemos ahora los objetos finales numéricos.
Nuevamente use el ícono  , elija el elemento Elección de objetos finales numéricos.
, elija el elemento Elección de objetos finales numéricos.
Haga clic en n1 y luego haga clic en ang2 para obtener lo siguiente :
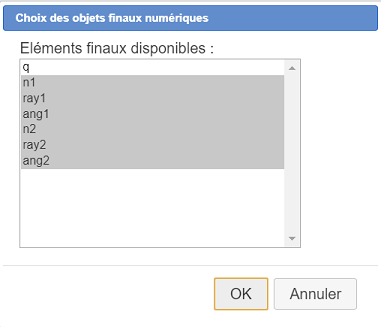
Quedan por elegir los objetos finales gráficos.
Nuevamente use el ícono  , elija el ítem Elección de objetos finales gráficos.
, elija el ítem Elección de objetos finales gráficos.
Haga clic en :
- los vectores $\overrightarrow{AB}$ y $\overrightarrow{AC}$
- Las dos visualizaciones de valores relacionados con los puntos medios de [AB] y [AC]
- Ambas visualizaciones LaTeX
- Los puntos D y E
Haga clic en el botón rojo STOP para indicar que ha terminado de designar los objetos finales gráficos.
Antes de terminar la construcción, oculte los puntos D y E con la herramienta  .
.
Todavía tenemos que finalizar nuestra construcción.
Nuevamente use el ícono  , elija el elemento Finalizar la construcción en curso.
, elija el elemento Finalizar la construcción en curso.
Rellene el cuadro de diálogo como se muestra a continuación. El campo Información se usa para informar al usuario cuando usa la construcción.
Aquí está su contenido si desea puede copiarlo y pegarlo :
#1:Valor de coefRay (coeficiente de reducción en cada etapa para la longitud de las flechas)
#2: Valor de coefAng (coeficiente de reducción en cada etapa para el ángulo de las flechas con la horizontal)
#3: Valor p (probabilidad de éxito)
#4: Valor de n (el rango de generación de rama)
#5: El radio inicial (longitud de las flechas)
#6: El ángulo inicial en grados de la primera flecha con la horizontal
##7: El punto de origen del árbol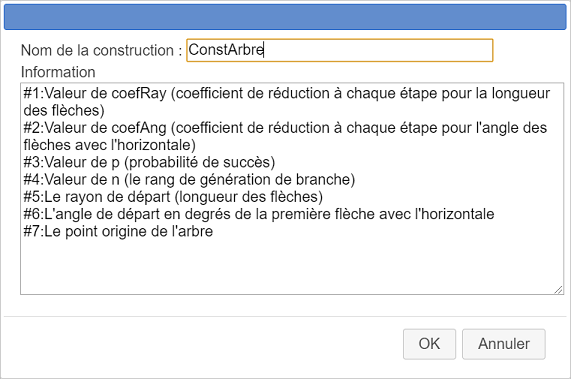
Guarde la figura en la ubicación que elija por seguridad. La llamaremos BinomialTree1.
Para guardar la construcción en un archivo separado, use el ícono  y elija el elemento Guardar una construcción de la figura. Guarde la construcción ConstArbre en la ubicación que elija.
y elija el elemento Guardar una construcción de la figura. Guarde la construcción ConstArbre en la ubicación que elija.
Algunas explicaciones : Esta construcción se implementará de forma recursiva. Los objetos fuentes deben aparecer en la figura primero en la lista de objetos creados. Estos son para nosotros : coefRay, coefAngle, p, n, ray, ang. Los tres primeros serán comunes a todas las implementaciones. El único objeto fuente gráfico es el punto inicial del árbol. Durante implementaciones sucesivas, los objetos fuentes no comunes serán reemplazados por los primeros objetos finales. La construcción se implementará nuevamente para n1, ray1, ang1, punto B, luego para n2, ray2, ang2, punto C y el paso será de 4 porque saltamos 4 objetos finales para ir de n1 a n2.
Cree una nueva figura que contendrá nuestra figura final (sin referencial y con longitud unidad). Verifique que esté usando el grado como unidad de ángulo.
Cree un punto libre en el medio y a la izquierda de la figura.
Cree los siguientes cálculos (en este orden) :
– Un cálculo llamado coefRay con la fórmula 0.7
– Un cálculo llamado coefAng con la fórmula 0.7
– Un cálculo llamado p con la fórmula 0.25
– Un cálculo llamado nbsDem con la fórmula 1 (solo se usará en la etepa 4)
– Un cálculo llamado n con la fórmula 0
– Un cálculo llamado ray con la fórmula 4.8
– Un cálculo llamado ang con la fórmula 45
Utilice nuevamente el ícono  , elija el ítem Incorporar una construcción desde un archivo e incorpore en esta figura la construcción ConstArbre.
, elija el ítem Incorporar una construcción desde un archivo e incorpore en esta figura la construcción ConstArbre.
Ahora crearemos una macro encargada de implementar esta construcción recursivamente.
Abra la barra de menú de visualizaciones y, a su derecha, haga clic en la herramienta  , y elija en la parte inferior de la lista Macro de implementación recursiva, luego haga clic en la parte superior izquierda de la figura para designar la ubicación de su título.
, y elija en la parte inferior de la lista Macro de implementación recursiva, luego haga clic en la parte superior izquierda de la figura para designar la ubicación de su título.
Complete el primer cuadro de diálogo como se muestra a continuación :
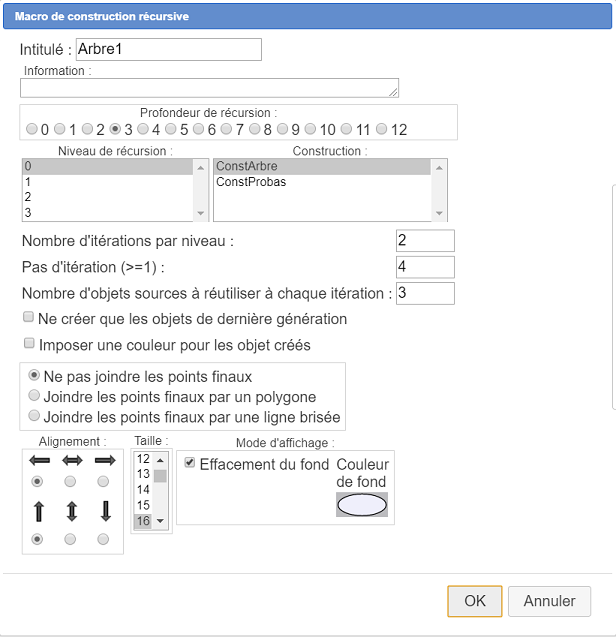
Se abre un segundo cuadro de diálogo. Debe asignar los objetos fuentes.
Asigne al objeto de origen número 1 el cálculo coefRay de la siguiente manera :
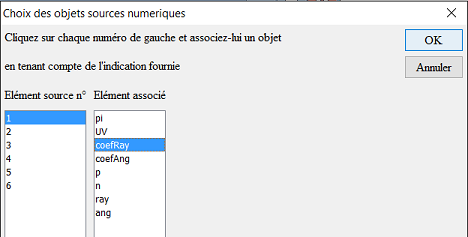
Del mismo modo asigne :
– Al elemento fuente n° 2 el cálculo coefAng
– Al elemento fuente n° 3 el cálculo p
– Al elemento fuente n° 4 el cálculo n
– Al elemento fuente n° 5 el cálculo ray
– Al elemento fuente n° 6 el cálculo ang
Validar. Ahora se le pide que haga clic en el punto de origen del árbol. Haga clic en el punto libre que creó.
Aparece la macro. Al hacer clic en su título, debería ver aparecer el árbol binomial. Si funciona, cancele la ejecución de esta macro (icono  ).
).
Guarde esta figura en la ubicación de su elección. Lo llamaremos ArbreBinomialFinal.
Retome la figura BinomialTree1. Vamos a modificarla para crear otra construcción que se encargará de mostrar las probabilidades al final de las ramas.
Utilice la herramienta  para desenmascarar los puntos D y E.
para desenmascarar los puntos D y E.
Use el ícono  para crear un nuevo cálculo llamado nbsDem que contenga como fórmula 1. Este cálculo formará parte de los objetos fuentes comunes a todas las implementaciones. Por lo tanto, debe ser reclasificado. Para ello, utilice el protocolo de la figura (icono
para crear un nuevo cálculo llamado nbsDem que contenga como fórmula 1. Este cálculo formará parte de los objetos fuentes comunes a todas las implementaciones. Por lo tanto, debe ser reclasificado. Para ello, utilice el protocolo de la figura (icono  de la barra superior).
de la barra superior).
Use las flechas de reclasificación de objetos ( y
y  ) de la derecha para tener inmediatamente nbsDem después del cálculo p . nbsDem representará el número deseado de éxitos.
) de la derecha para tener inmediatamente nbsDem después del cálculo p . nbsDem representará el número deseado de éxitos.
De manera similar, cree un nuevo cálculo llamado nbs con la fórmula 0 y use la herramienta de protocolo  para reclasificar nbs inmediatamente después del cálculo ang.
para reclasificar nbs inmediatamente después del cálculo ang.
Cree un cálculo llamado nbs1 que contenga como fórmula nbs+1 y use la herramienta de protocolo  para reclasificarlo justo después del cálculo ang1. nbs1 representa el número de éxitos al pasar a una rama superior.
para reclasificarlo justo después del cálculo ang1. nbs1 representa el número de éxitos al pasar a una rama superior.
Cree un cálculo denominado nbs2 que contenga la fórmula nbs y use la herramienta de protocolo  para reclasificarlo justo después del cálculo ang2. nbs2 representa el número de éxitos al pasar a una rama inferior.
para reclasificarlo justo después del cálculo ang2. nbs2 representa el número de éxitos al pasar a una rama inferior.
Usando el ícono use la herramienta Protocolo  cree los siguientes cálculos :
cree los siguientes cálculos :
- Un cálculo llamado nbe1 que contiene como fórmula n1-nbs1
- Un cálculo llamado nbe2 que contiene como fórmula n2-nbs2
- Un cálculo llamado pb1 que contiene como fórmula p^nbs1*q^nbe1
- Un cálculo llamado pb2 que contiene como fórmula p^nbs2*q^nbe2
- Un cálculo llamado test1 que contiene como fórmula nbs1=nbsDem
- Un cálculo llamado test2 que contiene como fórmula nbs2=nbsDem
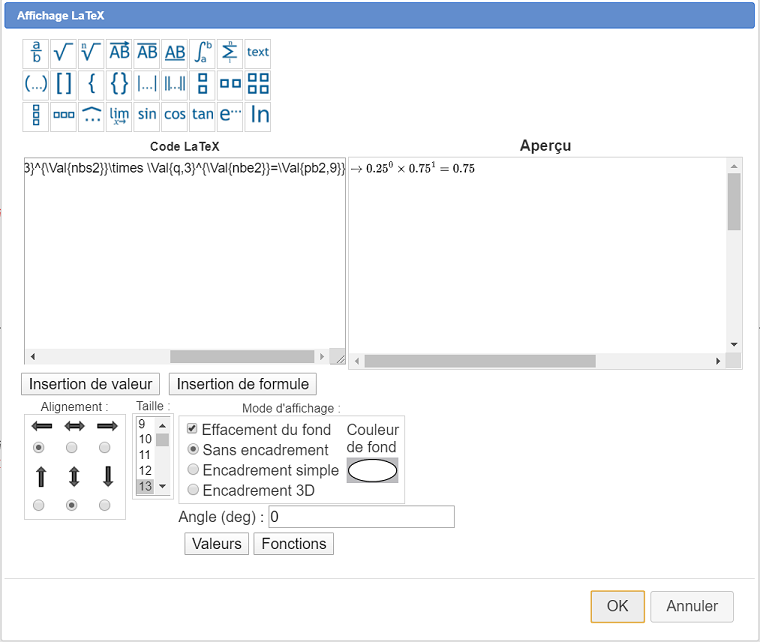
Ahora use la herramienta de icono  para crear una pantalla LaTeX ligada al punto D. Haga clic en el punto D y complete el cuadro de diálogo como se muestra a continuación. No olvide elegir el modo de alineación centrado horizontalmente y con la flecha izquierda para la alineación horizontal. El código LaTeX a introducir es el siguiente :
para crear una pantalla LaTeX ligada al punto D. Haga clic en el punto D y complete el cuadro de diálogo como se muestra a continuación. No olvide elegir el modo de alineación centrado horizontalmente y con la flecha izquierda para la alineación horizontal. El código LaTeX a introducir es el siguiente :
\textcolor{\If{test1}{red}{black}}{\rightarrow \Val{p,3}^{\Val{nbs1}}\times \Val{q,3}^{\Val{ nbe1}}=\Val{pb1,9}}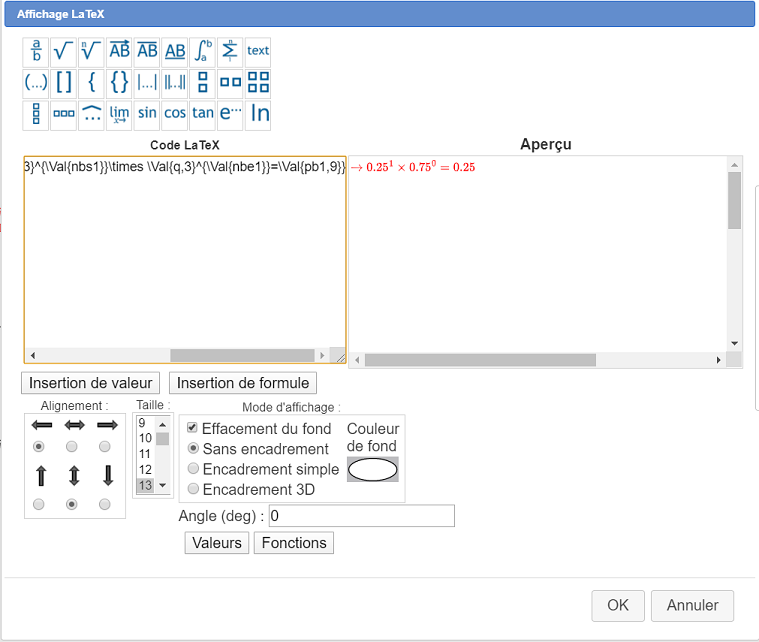
Ahora use el ícono  para crear una visualización LaTeX ligada al punto E. Haga clic en el punto E y complete el cuadro de diálogo como se muestra a continuación. No olvide elegir el modo de alineación centrado horizontalmente y con la flecha izquierda para la alineación horizontal. El código LaTeX para ingresar es :
para crear una visualización LaTeX ligada al punto E. Haga clic en el punto E y complete el cuadro de diálogo como se muestra a continuación. No olvide elegir el modo de alineación centrado horizontalmente y con la flecha izquierda para la alineación horizontal. El código LaTeX para ingresar es : \textcolor{\If{test2}{red}{black}}{\rightarrow \Val{p,3}^{\Val{nbs2}}\times \Val{ q, 3}^{\Val{nbe2}}=\Val{pb2,9}}
Utilice el icono  y elija el ítem Elección de objetos fuentes numéricos.
y elija el ítem Elección de objetos fuentes numéricos.
Elija como elementos de origen (en este orden) : coefRay, coefAng, p, nbsDem, n, ray, ang y nbs.
Nuevamente use el ícono  y elija el elemento Elección de objetos de origen gráfico.
y elija el elemento Elección de objetos de origen gráfico.
Haga clic en el punto A y luego haga clic en el botón rojo STOP para indicar que la elección de los objetos de origen gráfico ha finalizado.
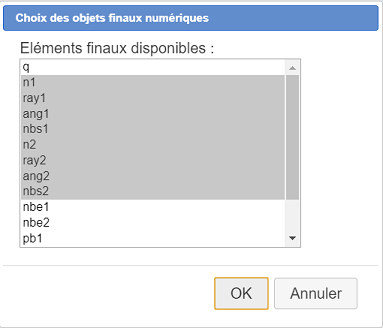
Nuevamente use el ícono  y elija el elemento Elección de objetos digitales finales. Seleccione los objetos finales digitales como se muestra a continuación.
y elija el elemento Elección de objetos digitales finales. Seleccione los objetos finales digitales como se muestra a continuación.
Utilice de nuevo el icono  y elija el elemento Elección de objetos gráficos finales. Haga clic en los puntos D y E y en las dos pantallas LaTeX vinculadas a D y E, luego haga clic en el botón rojo STOP.
y elija el elemento Elección de objetos gráficos finales. Haga clic en los puntos D y E y en las dos pantallas LaTeX vinculadas a D y E, luego haga clic en el botón rojo STOP.
Utilice el icono  para ocultar los puntos D y E.
para ocultar los puntos D y E.
Todavía tenemos que finalizar nuestra construcción.
Nuevamente use el ícono  y elija el elemento Finalizar la construcción actual.
y elija el elemento Finalizar la construcción actual.
Rellene el cuadro de diálogo como se muestra a continuación. Este es el contenido del campo Infos si desea copiarlo y pegarlo :
#1:Valor de coefRay (coeficiente de reducción en cada paso para la longitud de las flechas)
#2: Valor de coefAng (coeficiente de reducción en cada paso para el ángulo de las flechas con la horizontal)
#3: Valor p (probabilidad de éxito)
#4;Valor de nbsDem (número deseado de éxitos)
#5:Valor de n (el rango de generación de sucursales)
#6: El radio inicial (longitud de las flechas)
#7: El ángulo inicial en grados de la primera flecha con la horizontal
#8: El número de éxitos (debe inicializarse a cero)
#9:El punto de origen del eje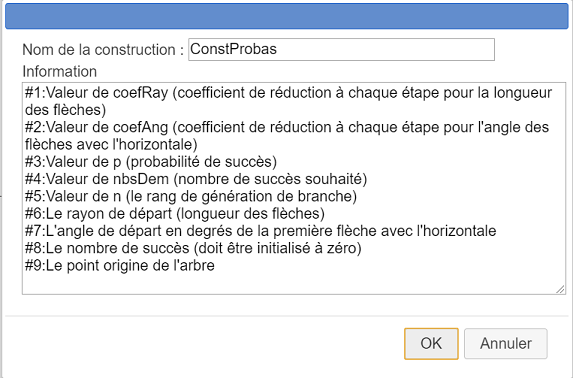
Por seguridad, guarde esta figura con el nombre ArbreBinomial2.
Utilice el icono  y elija el elemento Guardar una construcción de la figura. Guarde la construcción ConstProbas en una ubicación de su elección.
y elija el elemento Guardar una construcción de la figura. Guarde la construcción ConstProbas en una ubicación de su elección.
Regrese a la figura ArbreBinomial (que será nuestra figura final) en la que ya hemos creado una macro que implementa la construcción ConstArbre.
Utilice el icono  y elija el elemento Incorporar una construcción desde un archivo. Obtenga la construcción ConstProbas desde donde la guardó.
y elija el elemento Incorporar una construcción desde un archivo. Obtenga la construcción ConstProbas desde donde la guardó.
Vamos a agregarle una macro implementando la construcción ConstProbas.
Expanda la barra de herramientas de visualizaciones y, a su derecha, haga clic en el icono  . Elija el elemento Macro de construcción recursiva.
. Elija el elemento Macro de construcción recursiva.
Haga clic en la parte superior izquierda de la figura para designar la ubicación de su título.
Complete el primer cuadro de diálogo como se muestra a continuación. Tenga cuidado de asignar la macro ConstProbas a cada nivel de recursión y marque la casilla Solo crear objetos de última generación. Cuando esta construcción se implemente recursivamente, no se crearán para los niveles intermedios objetos finales que no sean los utilizados para implementar la próxima generación. Es solo para la última generación que se implementarán todos los objetos finales. Por lo tanto, las visualizacioness de LaTeX que contienen las probabilidades solo se implementarán para las ramas finales del árbol.
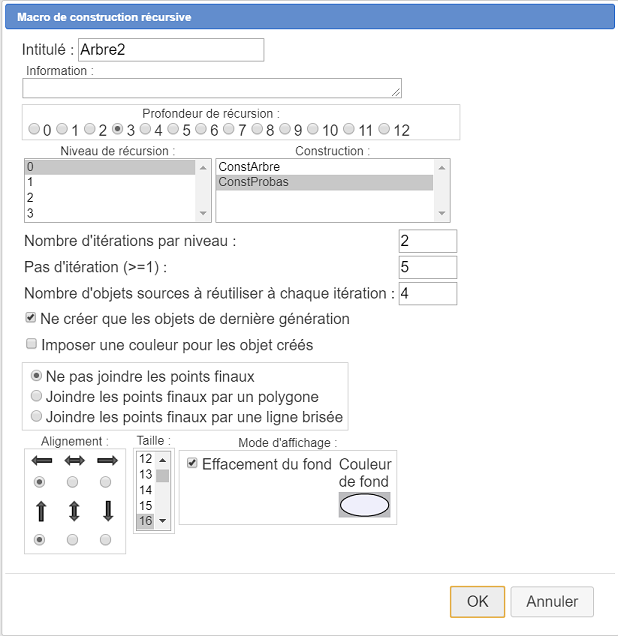
Aparece un nuevo cuadro de diálogo para asignar los objetos de fuentes numéricos.
- Asignar al elemento n° 1 el cálculo coefRay
- Asignar al elemento n° 2 el cálculo coefAng
- Asignar al elemento n° 3 el cálculo p
- Asignar al elemento n° 4 el cálculo nbsDem
- Asignar al elemento n° 5 el cálculo n
- Asignar al elemento n° 6 el cálculo ray
- Asignar al elemento n° 7 el cálculo ang
- Asignar al elemento n° 8 el cálculo nbs
Ahora se le pide que haga clic en el punto de origen del árbol. Haga clic en el mismo punto libre que para la primera macro.
Haga clic en cada una de las dos macros para ejecutarlas. Debería ver aparecer el árbol completo y, al final de las ramas, las probabilidades en rojo cuando el número de aciertos es nbsDem (por el momento igual a 1) y en negro en los demás casos.
Para completar esta figura crearemos un cursor que representará el número de aciertos solicitados.
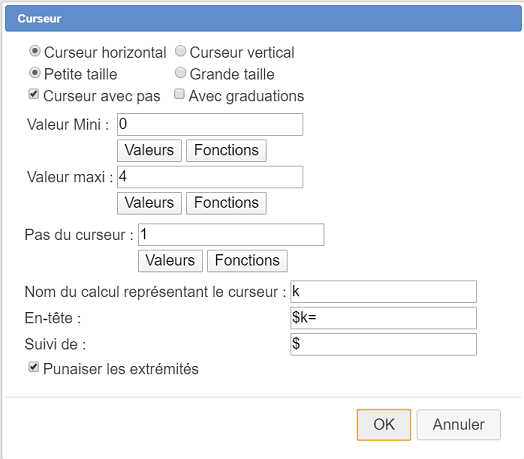
Utilice el icono  para crear un cursor de valores enteros como el siguiente.
para crear un cursor de valores enteros como el siguiente.
En la barra de herramientas superior, active la herramienta  utilizada para modificar o reclasificar objetos numéricos.
utilizada para modificar o reclasificar objetos numéricos.
Haga clic en k (que aparece al final de la lista) y luego haga clic en el botón Reclasificar hacia el comienzo.
Ahora nbsDem podrá usar el valor de k.
Haga clic en nbsDem y luego haga clic en el botón Modificar. Ingrese como fórmula k.
Haga clic en el botón Cerrar para cerrar el cuadro de diálogo.
Cuando captura el cursor, ve que se actualizan las probabilidades de final de rama.
Utilice el icono  para crear :
para crear :
- un nuevo cálculo llamado q que contiene como fórmula 1-p
- un nuevo cálculo llamado coeBin que contiene como fórmula nCr(4,k)
- un nuevo cálculo llamado k’ que contiene como fórmula 4-k
- un nuevo cálculo llamado pk que contiene como fórmula coebin*p^k*q^k'
Finalmente, crearemos una visualización LaTeX dando la probabilidad P(X=k) donde X es una variable aleatoria que sigue la distribución binomial con parámetros n=4 y p.
Use el ícono  , en la parte superior derecha del cursor ingrese como código LaTeX :
, en la parte superior derecha del cursor ingrese como código LaTeX :
P\left( X=k \right)=\left( \begin{matriz}{l} 4 \\\Val{k} \end{matriz} \right)\Val{p,3}^\Val{k }\times \left( 1-\Val{p,3} \right)^\Val{k'} = \Val{coebin}\times \Val{p,3}^\Val{k}\times \Val {q,3}^\Val{k'}\approx \Val{pk,9}La figura está terminada y puede usar la herramienta  para ocultar las dos macros.
para ocultar las dos macros.
A continuación se muestra la figura final :