Toutes les versions de cet article : [English] [Español] [français]
Depuis la version 6.7, MathGraph32 permet de créer et calculer des matrices à coefficients réels.
Dans ce premier tutoriel, nous allons expliquer des fonctionnalités de base sur un exemple.
Commencez par créer à l’aide de l’icône  une nouvelle figure sans repère et sans longueur unité.
une nouvelle figure sans repère et sans longueur unité.
Déroulez la barre d’outil des calculs (la troisième en partant du bas) et cliquez à sa droite sur l’icône  .
.
Choisissez Matrice dans la liste déroulante. Ceci permet de créer une matrice en donnant son nombre de lignes et de colonnes et en entrant une formule pour chaque élément de la matrice.
Remplissez la boîte de dialogue comme ci-dessous :

Nous allons maintenant demander à MathGraph32 de calculer le déterminant de cette matrice.
Déroulez à nouveau la barre d’outil des calculs (la troisième en partant du bas) et cliquez à sa droite sur l’icône  .
.
Choisissez Déterminant dans la liste déroulante et validez.
Une boîte de dialogue apparaît.
Dans la liste déroulante des matrices présentes, la matrice A est déjà sélectionnée. Entrez detA dans le champ Nom du calcul et validez.
Si vous utilisez l’icône  de la barre supérieure, vous verrez que detA a pour valeur - 6. Vous pouvez aussi utiliser l’icône
de la barre supérieure, vous verrez que detA a pour valeur - 6. Vous pouvez aussi utiliser l’icône ![]() pour afficher la valeur de detA sur la figure.
pour afficher la valeur de detA sur la figure.
Une autre façon de créer une matrice est de créer un calcul matriciel.
Avant cela vérifiez à l’aide de l’icône ![]() que votre figure utilise bien le radian.
que votre figure utilise bien le radian.
Utilisez à nouveau l’outil l’icône  dans la barre d’outil des calculs et cliquez sur Calcul matriciel.
dans la barre d’outil des calculs et cliquez sur Calcul matriciel.
Remplissez la boîte de dialogue comme ci-dessous :
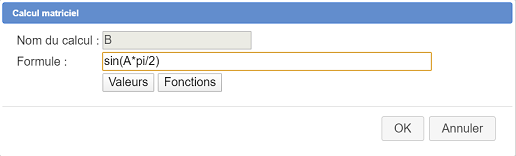
La formule à entrer est la suivante :
sin(A*pi/2)
Vous pouvez utiliser l’outil  pour voir la valeur de cette matrice.
pour voir la valeur de cette matrice.
Ce calcul matriciel commence à multiplier chacun des termes de la matrice A par pi/2 puis rend comme valeur la matrice formée du sinus de la matrice ainsi obtenue.
Nous allons maintenant demander un affichage de la valeur de cette matrice B à l’aide d’un affichage LaTeX.
Cliquez sur l’icône 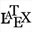 (affichage LaTeX libre), cliquez en haut et à gauche de la figure.
(affichage LaTeX libre), cliquez en haut et à gauche de la figure.
Pour entrer le code LaTeX suivant vous pouvez utiliser d’abord l’icône insérant le code LaTeX pour obtenir des parenthèses et cliquer sur le bouton Insertion de valeur pour choisir la matrice dont la valeur doit être affichée.
Voici le code LaTeX :
B=\left( \Val{B} \right)Créez maintenant un nouveau calcul matriciel nommé C avec comme formule la formule ci-dessous :
B^3Le résultat est donc la puissance troisième de B (soit B \times B \times B).
A noter que l’élévation d’une matrice à une puissance n’est valide que pour une matrice carrée (même nombre de lignes et de colonnes).
Affichez le résultat de cette matrice à l’aide d’un affichage LaTeX au-dessous de l’affichage LaTeX précédent.
Voici le code LaTeX à utiliser :
B^3=\left( \Val{C} \right)Nous allons maintenant utiliser une autre façon de créer une matrice, en donnant une formule permettant de définir les termes de la matrice en fonction de leur numéro de ligne i et de leur numéro de colonne j.
Utilisez à nouveau l’outil l’icône  dans la barre d’outil des calculs et cliquez sur Matrice par formule.
dans la barre d’outil des calculs et cliquez sur Matrice par formule.
Remplissez la boîte de dialogue comme ci-dessous :
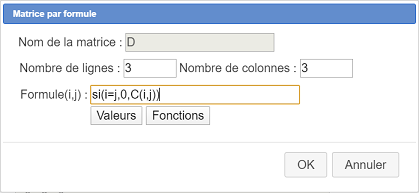
Voici le code de la formule à entrer :
si(i=j,0,C(i,j))Ainsi, si le numéro de ligne i est égal au numéro de colonne j, le terme de la matrice créée sera nul (termes de la diagonale) et pour les autres termes le terme de la matrice obtenue sera le même que le terme correspondant de la matrice C.
Vous pouvez afficher le résultat de cette nouvelle matrice à l’aide d’un nouveau affichage LaTeX ayant le code LaTeX suivant :
D=\left( \Val{D} \right)Nous voulons maintenant créer une matrice dont les termes soit les termes de la matrice D élevés au carré.
Créez de nouveau une matrice par formule de la façon suivante :
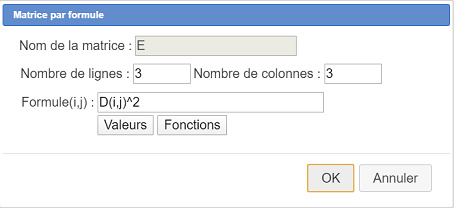
Voici ci-dessous le code de la formule à utiliser :
D(i,j)^2Vous pouvez afficher le résultat de cette nouvelle matrice à l’aide d’un nouveau affichage LaTeX ayant le code LaTeX suivant :
D=\left( \Val{E} \right)Attention : Un calcul matriciel avec comme formule D^2 ne produirait pas le même résultat car il rendrait comme valeur le produit matriciel de la matrice D par elle-même.
Créez maintenant un nouveau calcul matriciel nommé F avec comme formule :
D*ECe produit matriciel est valide car le nombre de colonnes de la première matrice D est égal au nombre de lignes de la deuxième matrice E.
Vous pouvez afficher le résultat de cette nouvelle matrice à l’aide d’un nouveau affichage LaTeX ayant le code LaTeX suivant :
D=\left( \Val{F} \right)Nous voulons maintenant créer une matrice colonne dont les termes soient ceux de la dernière colonne de la matrice D.
Créez une nouvelle matrice par formule nommée G comme ci-dessous :
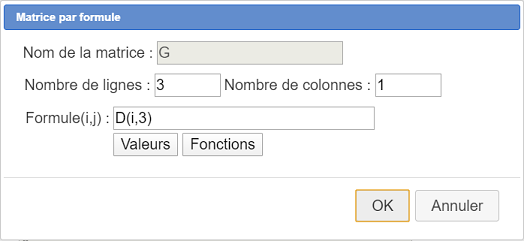
Voici la formule utilisée :
D(i,3)Vous pouvez afficher le résultat de cette nouvelle matrice à l’aide d’un nouveau affichage LaTeX ayant le code LaTeX suivant :
D=\left( \Val{G} \right)Créez maintenant un calcul matriciel nommé H défini par la formule suivante :
B*GLe résultat est une matrice colonne que vous pouvez afficher dans un affichage LaTeX à l’aide du code LaTeX suivant :
B \times G=\left( \Val{H} \right)Pour finir, montrons qu’un calcul matriciel peut donner un résultat qui n’est pas défini.
Créez un calcul matriciel nommé J avec la formule suivante :
G*BSi vous utilisez l’outil  de la barre d’outils supérieure vous verrez que ce calcul matriciel est déclaré comme non existant. En effet, le nombre de colonnes de la matrice G n’est pas égal au nombre de lignes de la matrice B.
de la barre d’outils supérieure vous verrez que ce calcul matriciel est déclaré comme non existant. En effet, le nombre de colonnes de la matrice G n’est pas égal au nombre de lignes de la matrice B.
Il et donc de votre résultat de vous assurer que vos calculs matriciels sont bien valides.
Voici ci-dessous le code base 64 de la figure finale :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAAAAAAAAAAAABT#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAIQ01hdHJpY2UA#####wABQQAAAAMAAAADAAAAAT#wAAAAAAAAAAAAAUAIAAAAAAAAAAAAAUAIAAAAAAAAAAAAAT#wAAAAAAAAAAAAAUAAAAAAAAAAAAAAAT#wAAAAAAAAAAAAAUAIAAAAAAAAAAAAAUAQAAAAAAAAAAAAAUAUAAAAAAAA#####wAAAAEAFENJbXBsZW1lbnRhdGlvblByb3RvAP####8ADETDqXRlcm1pbmFudAAAAAEAAAABAAAAAQAAAAH#####AAAAAQAIQ0NhbGNNYXQAAAAAAgAGZGV0TWF0AAhkZXRlcihBKf####8AAAACAAlDRm9uY3Rpb24X#####wAAAAEAD0NSZXN1bHRhdFZhbGV1cgAAAAH#####AAAAAQAHQ0NhbGN1bAEAAAACAARkZXRBAAtkZXRNYXQoMSwxKf####8AAAABAAhDVGVybU1hdAAAAAMAAAABP#AAAAAAAAAAAAABP#AAAAAAAAAAAAAEAP####8AAUIAC3NpbihBKnBpLzIpAAAABQP#####AAAAAQAKQ09wZXJhdGlvbgMAAAAJAgAAAAYAAAABAAAABgAAAAAAAAABQAAAAAAAAAD#####AAAAAgAGQ0xhdGV4AP####8AAAAAAQAA#####xBAMIAAAAAAAEAtCj1wo9cMAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAYQj1cbGVmdCggXFZhbHtCfSBccmlnaHQpAAAABAD#####AAFDAANCXjP#####AAAAAQAKQ1B1aXNzYW5jZQAAAAYAAAAFAAAAAUAIAAAAAAAAAAAACgD#####AAAAAAEAAP####8QQCcAAAAAAABAWWFHrhR64gAAAAAAAAAAAAAAAAABAAAAAAAAAAAAGkJeMz1cbGVmdCggXFZhbHtDfSBccmlnaHQp#####wAAAAEAD0NNYXRyaWNlUGFyRm9ybQD#####AAFEAAAAAwAAAAP#####AAAAAQANQ0ZvbmN0aW9uM1ZhcgAAAAAJCP####8AAAACABFDVmFyaWFibGVGb3JtZWxsZQAAAAAAAAAOAAAAAQAAAAEAAAAAAAAAAAAAAAgAAAAHAAAADgAAAAAAAAAOAAAAAQAAAAoA#####wAAAAABAAD#####EEAnAAAAAAAAQGbQo9cKPXEAAAAAAAAAAAAAAAAAAQAAAAAAAAAAABhEPVxsZWZ0KCBcVmFse0R9IFxyaWdodCkAAAAMAP####8AAUUAAAADAAAAAwAAAAsAAAAIAAAACQAAAA4AAAAAAAAADgAAAAEAAAABQAAAAAAAAAAAAAAKAP####8AAAAAAQAA#####xBAKQAAAAAAAEBwmFHrhR64AAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAYRT1cbGVmdCggXFZhbHtFfSBccmlnaHQpAAAABAD#####AAFGAANEKkUAAAAJAgAAAAYAAAAJAAAABgAAAAsAAAAKAP####8AAAAAAQAA#####xBAJwAAAAAAAEB2aFHrhR64AAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAjRCBcdGltZXMgRSA9IFxsZWZ0KCBcVmFse0Z9IFxyaWdodCkAAAAMAP####8AAUcAAAADAAAAAQAAAAgAAAAJAAAADgAAAAAAAAABQAgAAAAAAAAAAAAKAP####8AAAAAAQAA#####xBAKQAAAAAAAEB7aFHrhR64AAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAYRz1cbGVmdCggXFZhbHtHfSBccmlnaHQpAAAABAD#####AAFIAANCKkcAAAAJAgAAAAYAAAAFAAAABgAAAA8AAAAKAP####8AAAAAAQAA#####xBAYJAAAAAAAEB7yFHrhR64AAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAhQiBcdGltZXMgRz1cbGVmdCggXFZhbHtIfSBccmlnaHQpAAAABAD#####AAFKAANHKkIAAAAJAgAAAAYAAAAPAAAABgAAAAX###############8=