Toutes les versions de cet article : [English] [Español] [Español] [français]
In this second tutorial about matrices, we will create a figure purpose of which is to solve a linear system of three equations with three unknown x, y and z (with integer coefficients).
For this, you must use 6.7.3 version of MathGraph32 at least.
To avoid fastidious steps, you will start from a figure already prepared.
In the upper toolbar, click on icon  and use Figure through Base 64 code.
and use Figure through Base 64 code.
Use the Base 64 code below :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAAAAAAAAQAAABr#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AANhMTEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2ExMgABNQAAAAFAFAAAAAAAAAAAAAIA#####wADYTEzAAEzAAAAAUAIAAAAAAAAAAAAAgD#####AANhMjEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2EyMgABMQAAAAE#8AAAAAAAAAAAAAIA#####wADYTIzAAEzAAAAAUAIAAAAAAAAAAAAAgD#####AANhMzEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2EzMgABMQAAAAE#8AAAAAAAAAAAAAIA#####wADYTMzAAEyAAAAAUAAAAAAAAAAAAAAAgD#####AAJiMQABMQAAAAE#8AAAAAAAAAAAAAIA#####wACYjIAATIAAAABQAAAAAAAAAAAAAACAP####8AAmIzAAEzAAAAAUAIAAAAAAAA#####wAAAAQAD0NFZGl0ZXVyRm9ybXVsZQD#####AAAAAAEAAP####8OQEdAAAAAAABAOYUeuFHrhgAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAABAAkkYV97MTF9PSQAAAAEAAEAAT0BAQAAAAMA#####wAAAAABAAD#####DkBn8AAAAAAAQDmFHrhR64YAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAAAgAJJGFfezEyfT0kAAAABAABAAE9AQEAAAADAP####8AAAAAAQAA#####w5AdVgAAAAAAEA3hR64UeuGAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAMACSRhX3sxM309JAAAAAQAAQABPQEBAAAAAwD#####AAAAAAEAAP####8OQEdAAAAAAABAUWFHrhR64gAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAEAAkkYV97MjF9PSQAAAAEAAEAAT0BAQAAAAMA#####wAAAAABAAD#####DkBn8AAAAAAAQFFhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAABQAJJGFfezIyfT0kAAAABAABAAE9AQEAAAADAP####8AAAAAAQAA#####w5AdVgAAAAAAEBQYUeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAYACSRhX3syM309JAAAAAQAAQABPQEBAAAAAwD#####AAAAAAEAAP####8OQEdAAAAAAABAXGFHrhR64gAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAHAAkkYV97MzF9PSQAAAAEAAEAAT0BAQAAAAMA#####wAAAAABAAD#####DkBn0AAAAAAAQFvhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAACAAJJGFfezMyfT0kAAAABAABAAE9AQEAAAADAP####8AAAAAAQAA#####w5AdUgAAAAAAEBa4UeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAkACSRhX3szM309JAAAAAQAAQABPQEBAAAAAwD#####AAAAAAEAAP####8OQH6oAAAAAABAOIUeuFHrhgAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAKAAYkYl8xPSQAAAAEAAEAAT0BAQAAAAMA#####wAAAAABAAD#####DkB+mAAAAAAAQFAhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAACwAGJGJfMj0kAAAABAABAAE9AQEAAAADAP####8AAAAAAQAA#####w5AfpgAAAAAAEBaIUeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAwABiRiXzM9JAAAAAQAAQABPQEB#####wAAAAIADENDb21tZW50YWlyZQD#####AP8AAAEAAP####8QQDOAAAAAAABAeKhR64UeuAAAAAAAAAAAAAAAAAABAAAAAAAAAAAA1kVudGVyIG9ubHkgaW50ZWdlciBudW1iZXJzIGFzIGNvZWZmaWNlbnRzLgpUaGUgc29sdXRpb24gd2lsbCBzdGlsbCBiZSBhY2N1cmF0ZSBpZiB0aGUgY29lZmZpY2ljZW50cwphcmUgcmF0aW9uYWwgbnVtYmVycyBidXQgdGhlIGRpc3BsYXkgb2YgdGhlIHN5dGVtCndpbGwgYmUgYXBwcm94aW1hdGVkIChpZiB0aGUgY29lZmZpY2llbnRzIHJlbWFpbgpzaW1wbGUgZW5vdWdoKS7###############8=In this figure have been prepared calculations $a_{11},a_{12},a_{13},a_{21},a_{22},a_{23},a_{31},a_{32},a_{33}$ which are the coefficients of the system and calculations $b_1,b_2,b_3$ which are the right constant terms of the system.
This figure also contains formula editors associated with each coefficient.
Now we wish to display the system to be solved via a LaTeX display.
For this we will use three real functions of three variables.
Expand the calculation toolbar and click on it’s right side on icon  .
.
In the list, choose Real function of three variables and fill in the dialog box as underneath :
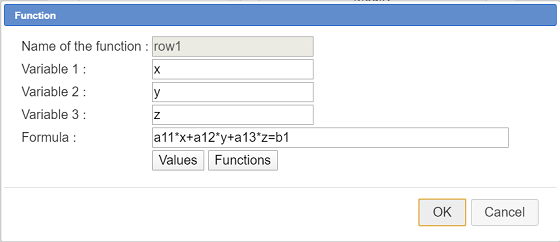
Here is the formula for function row1 :
a11*x+a12*y+a13*z=b1
Proceed in the same way to create a real function of three variables namedrow2 with this formula :
a21*x+a22*y+a23*z=b2
And again a function of three variables named row3 with this formula :
a31*x+a32*y+a33*z=b3
Now we are going to use a LaTeX display to display the system to be solved.
Expand the display toolbar and click on icon 
Click under the formula editors on the left side of the figure and use the LaTeX code below (you can use button  and click on button Formula insertion).
and click on button Formula insertion).
LaTeX code :
\text{Système : }
\left\{ \begin{array}{l}
\ForSimp{row1}
\\ \ForSimp{row2}
\\ \ForSimp{row3}
\end{array} \right.Now let us create a matrix A terms of which will be the system coefficients.
Expand the calculation toolbar and click on it’s right side on icon  .
.
In the list, choose Matrix and fill in the dialog box as below to create matrix A.

In the same way create a matrix B as shown above :
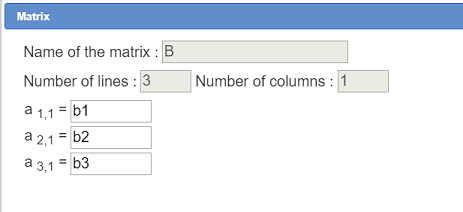
So the system to be solved is A \times X = B where X is the unknown matrix.
In order to know if this system has an single solution we are going to ask for the determinant of matrixA.
Expand the calculation toolbar and click on it’s right side on icon  .
.
In the list, choose Determinant and fill in the dialog box as underneath (the chosen name for the derminant will be detA).
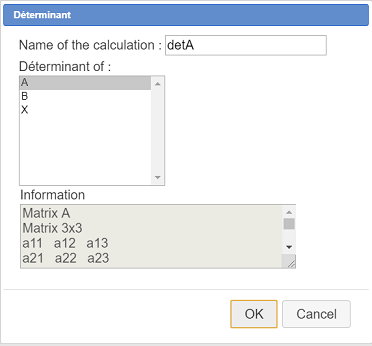
Expand the calculation toolbar and click on icon  to create a real calculation named detnul with this formula :
to create a real calculation named detnul with this formula :
detA=0
Now we will create a matrix calculation named X contanining the system’s solution when this solution is unique.
Expand the calculation toolbar and click on it’s right side on icon  .
.
In the list, choose Matricial calculation and fill in the dialog box as underneath.
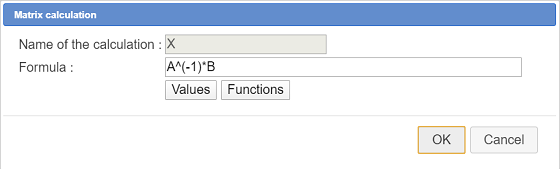
The name of the matrix calculation is X and the formula to be used is :
A^(-1)*B
A^(-1) represents the inverse matrix of matrix A (if A is inversible).
All we have got to do now is display the solution in a LaTeX display.
This LaTeX display will use a conditional display \If according to detnul. If detnul value is 1 the contents of the first brackets will be displayed and otherwise the contents of the second brackets will be used.
Expand the display toolbar and click on icon  .
.
Click under the former LaTeX display and use the LaTeX code above :
\If{detnul}
{
\text{The system has not a unique solution}
}
{
\begin{array}{l}
\text{The system has an unique solution}
\\ \left( \begin{array}{l}
x
\\ y
\\ z
\end{array} \right)
= \left( \ValFrac{X} \right)
\end{array}
}To be noted : this LaTeX display uses a special LaTeX code of MathGraph32 \ValFrac.
This code displays the matrix A where each cell is replaced by it’s rational approximated value (with 10^(-12) uncertainty). So, if the coefficients are not too big, the solution displayed is accurate.
Here is the Base 64 code of the final figure :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAAAAAAAAQAAACb#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AANhMTEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2ExMgABNQAAAAFAFAAAAAAAAAAAAAIA#####wADYTEzAAEzAAAAAUAIAAAAAAAAAAAAAgD#####AANhMjEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2EyMgABMQAAAAE#8AAAAAAAAAAAAAIA#####wADYTIzAAEzAAAAAUAIAAAAAAAAAAAAAgD#####AANhMzEAATEAAAABP#AAAAAAAAAAAAACAP####8AA2EzMgABMQAAAAE#8AAAAAAAAAAAAAIA#####wADYTMzAAEyAAAAAUAAAAAAAAAAAAAAAgD#####AAJiMQABMQAAAAE#8AAAAAAAAAAAAAIA#####wACYjIAATIAAAABQAAAAAAAAAAAAAACAP####8AAmIzAAEzAAAAAUAIAAAAAAAA#####wAAAAEACUNGb25jTlZhcgD#####AARyb3cxABRhMTEqeCthMTIqeSthMTMqej1iMf####8AAAABAApDT3BlcmF0aW9uCAAAAAQAAAAABAAAAAAEAv####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAAB#####wAAAAIAEUNWYXJpYWJsZUZvcm1lbGxlAAAAAAAAAAQCAAAABQAAAAIAAAAGAAAAAQAAAAQCAAAABQAAAAMAAAAGAAAAAgAAAAUAAAAKAAAAAwABeAABeQABegAAAAMA#####wAEcm93MgAUYTIxKngrYTIyKnkrYTIzKno9YjIAAAAECAAAAAQAAAAABAAAAAAEAgAAAAUAAAAEAAAABgAAAAAAAAAEAgAAAAUAAAAFAAAABgAAAAEAAAAEAgAAAAUAAAAGAAAABgAAAAIAAAAFAAAACwAAAAMAAXgAAXkAAXoAAAADAP####8ABHJvdzMAFGEzMSp4K2EzMip5K2EzMyp6PWIzAAAABAgAAAAEAAAAAAQAAAAABAIAAAAFAAAABwAAAAYAAAAAAAAABAIAAAAFAAAACAAAAAYAAAABAAAABAIAAAAFAAAACQAAAAYAAAACAAAABQAAAAwAAAADAAF4AAF5AAF6#####wAAAAQAD0NFZGl0ZXVyRm9ybXVsZQD#####AAAAAAEAAP####8OQEdAAAAAAABAOYUeuFHrhgAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAABAAkkYV97MTF9PSQAAAAEAAEAAT0BAQAAAAcA#####wAAAAABAAD#####DkBn8AAAAAAAQDmFHrhR64YAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAAAgAJJGFfezEyfT0kAAAABAABAAE9AQEAAAAHAP####8AAAAAAQAA#####w5AdVgAAAAAAEA3hR64UeuGAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAMACSRhX3sxM309JAAAAAQAAQABPQEBAAAABwD#####AAAAAAEAAP####8OQEdAAAAAAABAUWFHrhR64gAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAEAAkkYV97MjF9PSQAAAAEAAEAAT0BAQAAAAcA#####wAAAAABAAD#####DkBn8AAAAAAAQFFhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAABQAJJGFfezIyfT0kAAAABAABAAE9AQEAAAAHAP####8AAAAAAQAA#####w5AdVgAAAAAAEBQYUeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAYACSRhX3syM309JAAAAAQAAQABPQEBAAAABwD#####AAAAAAEAAP####8OQEdAAAAAAABAXGFHrhR64gAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAHAAkkYV97MzF9PSQAAAAEAAEAAT0BAQAAAAcA#####wAAAAABAAD#####DkBn0AAAAAAAQFvhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAACAAJJGFfezMyfT0kAAAABAABAAE9AQEAAAAHAP####8AAAAAAQAA#####w5AdUgAAAAAAEBa4UeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAkACSRhX3szM309JAAAAAQAAQABPQEBAAAABwD#####AAAAAAEAAP####8OQH6oAAAAAABAOIUeuFHrhgAAAAAAAgAAAAAAAAABAAAAAAAAAAAAAAAKAAYkYl8xPSQAAAAEAAEAAT0BAQAAAAcA#####wAAAAABAAD#####DkB+mAAAAAAAQFAhR64UeuIAAAAAAAIAAAAAAAAAAQAAAAAAAAAAAAAACwAGJGJfMj0kAAAABAABAAE9AQEAAAAHAP####8AAAAAAQAA#####w5AfpgAAAAAAEBaIUeuFHriAAAAAAACAAAAAAAAAAEAAAAAAAAAAAAAAAwABiRiXzM9JAAAAAQAAQABPQEB#####wAAAAIABkNMYXRleAD#####AAAAAAEAAP####8QQC0AAAAAAABAY#Cj1wo9cQAAAAAAAAAAAAAAAAABAAAAAAAAAAAAc1x0ZXh0e1N5c3TDqG1lIDogfQpcbGVmdFx7IFxiZWdpbnthcnJheX17bH0KXEZvclNpbXB7cm93MX0gClxcIFxGb3JTaW1we3JvdzJ9ClxcIFxGb3JTaW1we3JvdzN9ClxlbmR7YXJyYXl9IFxyaWdodC7#####AAAAAQAIQ01hdHJpY2UA#####wABQQAAAAMAAAADAAAABQAAAAEAAAAFAAAAAgAAAAUAAAADAAAABQAAAAQAAAAFAAAABQAAAAUAAAAGAAAABQAAAAcAAAAFAAAACAAAAAUAAAAJAAAACQD#####AAFCAAAAAwAAAAEAAAAFAAAACgAAAAUAAAALAAAABQAAAAz#####AAAAAQAUQ0ltcGxlbWVudGF0aW9uUHJvdG8A#####wAMRMOpdGVybWluYW50AAAAAQAAAAEAAAABAAAAHf####8AAAABAAhDQ2FsY01hdAAAAAAfAAZkZXRNYXQACGRldGVyKEEp#####wAAAAIACUNGb25jdGlvbhcAAAAFAAAAHQAAAAIBAAAAHwAEZGV0QQALZGV0TWF0KDEsMSn#####AAAAAQAIQ1Rlcm1NYXQAAAAgAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAAAAAAAgD#####AAZkZXRudWwABmRldEE9MAAAAAQIAAAABQAAACEAAAABAAAAAAAAAAAAAAALAP####8AAVgACEFeKC0xKSpCAAAABAL#####AAAAAQAKQ1B1aXNzYW5jZQAAAAUAAAAd#####wAAAAEADENNb2luc1VuYWlyZQAAAAE#8AAAAAAAAAAAAAUAAAAeAAAACAD#####AAAAAAEAAP####8QQCkAAAAAAABAcShR64UeuAAAAAAAAAAAAAAAAAABAAAAAAAAAAAA31xJZntkZXRudWx9CnsKXHRleHR7VGhlIHN5c3RlbSBoYXMgbm90IGEgdW5pcXVlIHNvbHV0aW9ufQp9CnsKXGJlZ2lue2FycmF5fXtsfQpcdGV4dHtUaGUgc3lzdGVtIGhhcyBhbiB1bmlxdWUgc29sdXRpb259ClxcIFxsZWZ0KCBcYmVnaW57YXJyYXl9e2x9CnggClxcIHkKXFwgegpcZW5ke2FycmF5fSBccmlnaHQpCj0gIFxsZWZ0KCBcVmFsRnJhY3tYfSBccmlnaHQpClxlbmR7YXJyYXl9Cn3#####AAAAAgAMQ0NvbW1lbnRhaXJlAP####8A#wAAAQAA#####xBAM4AAAAAAAEB4qFHrhR64AAAAAAAAAAAAAAAAAAEAAAAAAAAAAADWRW50ZXIgb25seSBpbnRlZ2VyIG51bWJlcnMgYXMgY29lZmZpY2VudHMuClRoZSBzb2x1dGlvbiB3aWxsIHN0aWxsIGJlIGFjY3VyYXRlIGlmIHRoZSBjb2VmZmljaWNlbnRzCmFyZSByYXRpb25hbCBudW1iZXJzIGJ1dCB0aGUgZGlzcGxheSBvZiB0aGUgc3l0ZW0Kd2lsbCBiZSBhcHByb3hpbWF0ZWQgKGlmIHRoZSBjb2VmZmljaWVudHMgcmVtYWluCnNpbXBsZSBlbm91Z2gpLv###############w==You can see the final figure underneath (and use it) :