Toutes les versions de cet article : [English] [Español] [français]
En este tutorial vamos a realizar una figura donde podemos escribir un sistema de 4 ecuaciones con 4 incógnitas de forma natural y resolverlo.
A continuación se muestra la figura en acción :
Para crear esta figura se debe utilizar la versión 6.8.0 de MathGraph32 o posterior.
Si no se desea seguir todos los pasos, se puede abrir esta figura usando su código Base 64 como a continuación :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUqAAAC4AAAAQEAAAAAAAAAAQAAAEv#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAJQ0ZvbmNOVmFyAP####8ABWVxdWExAAUzKng9Mf####8AAAABAApDT3BlcmF0aW9uCAAAAAMCAAAAAUAIAAAAAAAA#####wAAAAIAEUNWYXJpYWJsZUZvcm1lbGxlAAAAAAAAAAE#8AAAAAAAAAAAAAQAAXgAAXkAAXoAAXQAAAACAP####8ABWVxdWEyAAV4K3k9MgAAAAMIAAAAAwAAAAAEAAAAAAAAAAQAAAABAAAAAUAAAAAAAAAAAAAABAABeAABeQABegABdAAAAAIA#####wAFZXF1YTMAB3greSt6PTMAAAADCAAAAAMAAAAAAwAAAAAEAAAAAAAAAAQAAAABAAAABAAAAAIAAAABQAgAAAAAAAAAAAAEAAF4AAF5AAF6AAF0AAAAAgD#####AAVlcXVhNAAJeCt5K3o9NC10AAAAAwgAAAADAAAAAAMAAAAABAAAAAAAAAAEAAAAAQAAAAQAAAACAAAAAwEAAAABQBAAAAAAAAAAAAAEAAAAAwAAAAQAAXgAAXkAAXoAAXT#####AAAABAAPQ0VkaXRldXJGb3JtdWxlAP####8AAAAAAQAA#####xBAVaAAAAAAAEAxhR64UeuGAAH###8AAAACAAAAAAAAAAEAAAAAAAAAAAAAAAEADEVxdWF0aW9uIDEgOgAAABQBAQACXCwBAQAAAAUA#####wAAAAABAAD#####EEBVoAAAAAAAQE5Cj1wo9cMAAf###wAAAAIAAAAAAAAAAQAAAAAAAAAAAAAAAgAMRXF1YXRpb24gMiA6AAAAFAEBAAJcLAEBAAAABQD#####AAAAAAEAAP####8QQFUgAAAAAABAWWFHrhR64gAB####AAAAAgAAAAAAAAABAAAAAAAAAAAAAAADAAxFcXVhdGlvbiAzIDoAAAAUAQEAAlwsAQEAAAAFAP####8AAAAAAQAA#####xBAVOAAAAAAAEBicKPXCj1xAAH###8AAAACAAAAAAAAAAEAAAAAAAAAAAAAAAQADEVxdWF0aW9uIDQgOgAAABQBAQACXCwBAQAAAAIA#####wADZGYxACxnYXVjaGUoZXF1YTEoeCx5LHosdCkpLWRyb2l0KGVxdWExKHgseSx6LHQpKQAAAAMB#####wAAAAIACUNGb25jdGlvbhT#####AAAAAQASQ0FwcGVsRm9uY3Rpb25OVmFyAAAABAAAAAEAAAAEAAAAAAAAAAQAAAABAAAABAAAAAIAAAAEAAAAAwAAAAYVAAAABwAAAAQAAAABAAAABAAAAAAAAAAEAAAAAQAAAAQAAAACAAAABAAAAAMAAAAEAAF4AAF5AAF6AAF0AAAAAgD#####AANkZjIALGdhdWNoZShlcXVhMih4LHkseix0KSktZHJvaXQoZXF1YTIoeCx5LHosdCkpAAAAAwEAAAAGFAAAAAcAAAAEAAAAAgAAAAQAAAAAAAAABAAAAAEAAAAEAAAAAgAAAAQAAAADAAAABhUAAAAHAAAABAAAAAIAAAAEAAAAAAAAAAQAAAABAAAABAAAAAIAAAAEAAAAAwAAAAQAAXgAAXkAAXoAAXQAAAACAP####8AA2RmMwAsZ2F1Y2hlKGVxdWEzKHgseSx6LHQpKS1kcm9pdChlcXVhMyh4LHkseix0KSkAAAADAQAAAAYUAAAABwAAAAQAAAADAAAABAAAAAAAAAAEAAAAAQAAAAQAAAACAAAABAAAAAMAAAAGFQAAAAcAAAAEAAAAAwAAAAQAAAAAAAAABAAAAAEAAAAEAAAAAgAAAAQAAAADAAAABAABeAABeQABegABdAAAAAIA#####wADZGY0ACxnYXVjaGUoZXF1YTQoeCx5LHosdCkpLWRyb2l0KGVxdWE0KHgseSx6LHQpKQAAAAMBAAAABhQAAAAHAAAABAAAAAQAAAAEAAAAAAAAAAQAAAABAAAABAAAAAIAAAAEAAAAAwAAAAYVAAAABwAAAAQAAAAEAAAABAAAAAAAAAAEAAAAAQAAAAQAAAACAAAABAAAAAMAAAAEAAF4AAF5AAF6AAF0#####wAAAAEABUNGb25jAP####8ABHplcm8AEmFicyh4KTwwLjAwMDAwMDAwMQAAAAMEAAAABgAAAAAEAAAAAAAAAAE+ES4L6CbWlQABeP####8AAAABABFDRGVyaXZlZVBhcnRpZWxsZQD#####AAVkZXJ4MQAAAAkAAAAAAAAACQD#####AAVkZXJ5MQAAAAkAAAABAAAACQD#####AAVkZXJ6MQAAAAkAAAACAAAACQD#####AAVkZXJ0MQAAAAkAAAADAAAACQD#####AAVkZXJ4MgAAAAoAAAAAAAAACQD#####AAVkZXJ5MgAAAAoAAAABAAAACQD#####AAVkZXJ6MgAAAAoAAAACAAAACQD#####AAVkZXJ0MgAAAAoAAAADAAAACQD#####AAVkZXJ4MwAAAAsAAAAAAAAACQD#####AAVkZXJ5MwAAAAsAAAABAAAACQD#####AAVkZXJ6MwAAAAsAAAACAAAACQD#####AAVkZXJ0MwAAAAsAAAADAAAACQD#####AAVkZXJ4NAAAAAwAAAAAAAAACQD#####AAVkZXJ5NAAAAAwAAAABAAAACQD#####AAVkZXJ6NAAAAAwAAAACAAAACQD#####AAVkZXJ0NAAAAAwAAAAD#####wAAAAEACENNYXRyaWNlAP####8AAUEAAAAEAAAABAAAAAcAAAAEAAAADgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAADwAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAEAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAEQAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAEgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAEwAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAFAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAFQAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAFgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAFwAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAGAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAGQAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAGgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAGwAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAHAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAcAAAAEAAAAHQAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAP####8AAAABABRDSW1wbGVtZW50YXRpb25Qcm90bwD#####AAxEw6l0ZXJtaW5hbnQAAAABAAAAAQAAAAEAAAAe#####wAAAAEACENDYWxjTWF0AAAAAB8ABmRldE1hdAAIZGV0ZXIoQSkAAAAGF#####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAAe#####wAAAAEAB0NDYWxjdWwBAAAAHwAEZGV0QQALZGV0TWF0KDEsMSn#####AAAAAQAIQ1Rlcm1NYXQAAAAgAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAAAAAACgD#####AAFCAAAABAAAAAH#####AAAAAQAMQ01vaW5zVW5haXJlAAAABwAAAAQAAAAJAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAEAAAAAcAAAAEAAAACgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAABAAAAAHAAAABAAAAAsAAAABAAAAAAAAAAAAAAABAAAAAAAAAAAAAAABAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAQAAAABwAAAAQAAAAMAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAADAD#####AAFYAAhBXigtMSkqQgAAAAMC#####wAAAAEACkNQdWlzc2FuY2UAAAANAAAAHgAAABAAAAABP#AAAAAAAAAAAAANAAAAIgAAAA4A#####wACeDAABlgoMSwxKQAAAA8AAAAjAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAAAAAADgD#####AAJ5MAAGWCgyLDEpAAAADwAAACMAAAABQAAAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AAnowAAZYKDMsMSkAAAAPAAAAIwAAAAFACAAAAAAAAAAAAAE#8AAAAAAAAAAAAA4A#####wACdDAABlgoNCwxKQAAAA8AAAAjAAAAAUAQAAAAAAAAAAAAAT#wAAAAAAAAAAAADgD#####AAJ4MQAJMStyYW5kKDApAAAAAwAAAAABP#AAAAAAAAAAAAAGEQAAAAEAAAAAAAAAAD#JDHdg9gPoAAAADgD#####AAJ4MgAJMStyYW5kKDApAAAAAwAAAAABP#AAAAAAAAAAAAAGEQAAAAEAAAAAAAAAAD#HAt+KIoUAAAAADgD#####AAJ4MwAJMStyYW5kKDApAAAAAwAAAAABP#AAAAAAAAAAAAAGEQAAAAEAAAAAAAAAAD#eTQz86A48AAAADgD#####AAJ5MQALMS4xK3JhbmQoMCkAAAADAAAAAAE#8ZmZmZmZmgAAAAYRAAAAAQAAAAAAAAAAP+#hQopY9IYAAAAOAP####8AAnkyAAsxLjErcmFuZCgwKQAAAAMAAAAAAT#xmZmZmZmaAAAABhEAAAABAAAAAAAAAAA#5J9Nyyx5QAAAAA4A#####wACeTMACzEuMStyYW5kKDApAAAAAwAAAAABP#GZmZmZmZoAAAAGEQAAAAEAAAAAAAAAAD#RvtgjCkF8AAAADgD#####AAJ6MQALMS4yK3JhbmQoMCkAAAADAAAAAAE#8zMzMzMzMwAAAAYRAAAAAQAAAAAAAAAAP+j5izV8TtgAAAAOAP####8AAnoyAAsxLjIrcmFuZCgwKQAAAAMAAAAAAT#zMzMzMzMzAAAABhEAAAABAAAAAAAAAAA#7jiEgUIJrgAAAA4A#####wACejMACzEuMityYW5kKDApAAAAAwAAAAABP#MzMzMzMzMAAAAGEQAAAAEAAAAAAAAAAD#qVqFAND+8AAAADgD#####AAJ0MQALMS4zK3JhbmQoMCkAAAADAAAAAAE#9MzMzMzMzQAAAAYRAAAAAQAAAAAAAAAAP7o#KkKMDIAAAAAOAP####8AAnQyAAsxLjMrcmFuZCgwKQAAAAMAAAAAAT#0zMzMzMzNAAAABhEAAAABAAAAAAAAAAA#1mu2NjNTfAAAAA4A#####wACdDMACzEuMytyYW5kKDApAAAAAwAAAAABP#TMzMzMzM0AAAAGEQAAAAEAAAAAAAAAAD+wy1zsOJ1QAAAADgD#####AARkZWcxAV96ZXJvKGRlcngxKHgxLHkxLHoxLHQxKS1kZXJ4MSh4Mix5Mix6Mix0MikpJnplcm8oZGVyeDEoeDIseTIsejIsdDIpLWRlcngxKHgzLHkzLHozLHQzKSkmemVybyhkZXJ5MSh4MSx5MSx6MSx0MSktZGVyeTEoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcnkxKHgyLHkyLHoyLHQyKS1kZXJ5MSh4Myx5Myx6Myx0MykpJnplcm8oZGVyejEoeDEseTEsejEsdDEpLWRlcnoxKHgyLHkyLHoyLHQyKSkmemVybyhkZXJ6MSh4Mix5Mix6Mix0MiktZGVyejEoeDMseTMsejMsdDMpKSZ6ZXJvKGRlcnQxKHgxLHkxLHoxLHQxKS1kZXJ0MSh4Mix5Mix6Mix0MikpJnplcm8oZGVydDEoeDIseTIsejIsdDIpLWRlcnQxKHgzLHkzLHozLHQzKSkAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCv####8AAAABAA5DQXBwZWxGb25jdGlvbgAAAA0AAAADAQAAAAcAAAAEAAAADgAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAAOAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAAOAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAAA4AAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAABIAAAANAAAAAwEAAAAHAAAABAAAAA8AAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAADwAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAADwAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAPAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAASAAAADQAAAAMBAAAABwAAAAQAAAAQAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABAAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABAAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAEAAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAEQAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAARAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAARAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAABEAAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAAA4A#####wAEZGVnMgFfemVybyhkZXJ4Mih4MSx5MSx6MSx0MSktZGVyeDIoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcngyKHgyLHkyLHoyLHQyKS1kZXJ4Mih4Myx5Myx6Myx0MykpJnplcm8oZGVyeTIoeDEseTEsejEsdDEpLWRlcnkyKHgyLHkyLHoyLHQyKSkmemVybyhkZXJ5Mih4Mix5Mix6Mix0MiktZGVyeTIoeDMseTMsejMsdDMpKSZ6ZXJvKGRlcnoyKHgxLHkxLHoxLHQxKS1kZXJ6Mih4Mix5Mix6Mix0MikpJnplcm8oZGVyejIoeDIseTIsejIsdDIpLWRlcnoyKHgzLHkzLHozLHQzKSkmemVybyhkZXJ0Mih4MSx5MSx6MSx0MSktZGVydDIoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcnQyKHgyLHkyLHoyLHQyKS1kZXJ0Mih4Myx5Myx6Myx0MykpAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAASAAAADQAAAAMBAAAABwAAAAQAAAASAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABIAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABIAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAEgAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAEwAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAATAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAATAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAABMAAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAABIAAAANAAAAAwEAAAAHAAAABAAAABQAAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAAFAAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAFAAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAUAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAASAAAADQAAAAMBAAAABwAAAAQAAAAVAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABUAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABUAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAFQAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAADgD#####AARkZWczAV96ZXJvKGRlcngzKHgxLHkxLHoxLHQxKS1kZXJ4Myh4Mix5Mix6Mix0MikpJnplcm8oZGVyeDMoeDIseTIsejIsdDIpLWRlcngzKHgzLHkzLHozLHQzKSkmemVybyhkZXJ5Myh4MSx5MSx6MSx0MSktZGVyeTMoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcnkzKHgyLHkyLHoyLHQyKS1kZXJ5Myh4Myx5Myx6Myx0MykpJnplcm8oZGVyejMoeDEseTEsejEsdDEpLWRlcnozKHgyLHkyLHoyLHQyKSkmemVybyhkZXJ6Myh4Mix5Mix6Mix0MiktZGVyejMoeDMseTMsejMsdDMpKSZ6ZXJvKGRlcnQzKHgxLHkxLHoxLHQxKS1kZXJ0Myh4Mix5Mix6Mix0MikpJnplcm8oZGVydDMoeDIseTIsejIsdDIpLWRlcnQzKHgzLHkzLHozLHQzKSkAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCgAAABIAAAANAAAAAwEAAAAHAAAABAAAABYAAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAAFgAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAFgAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAWAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAASAAAADQAAAAMBAAAABwAAAAQAAAAXAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABcAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABcAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAFwAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAGAAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAAYAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAAYAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAABgAAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAABIAAAANAAAAAwEAAAAHAAAABAAAABkAAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAAGQAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAGQAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAZAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAAOAP####8ABGRlZzQBX3plcm8oZGVyeDQoeDEseTEsejEsdDEpLWRlcng0KHgyLHkyLHoyLHQyKSkmemVybyhkZXJ4NCh4Mix5Mix6Mix0MiktZGVyeDQoeDMseTMsejMsdDMpKSZ6ZXJvKGRlcnk0KHgxLHkxLHoxLHQxKS1kZXJ5NCh4Mix5Mix6Mix0MikpJnplcm8oZGVyeTQoeDIseTIsejIsdDIpLWRlcnk0KHgzLHkzLHozLHQzKSkmemVybyhkZXJ6NCh4MSx5MSx6MSx0MSktZGVyejQoeDIseTIsejIsdDIpKSZ6ZXJvKGRlcno0KHgyLHkyLHoyLHQyKS1kZXJ6NCh4Myx5Myx6Myx0MykpJnplcm8oZGVydDQoeDEseTEsejEsdDEpLWRlcnQ0KHgyLHkyLHoyLHQyKSkmemVybyhkZXJ0NCh4Mix5Mix6Mix0MiktZGVydDQoeDMseTMsejMsdDMpKQAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAGgAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAAaAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAAaAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAABoAAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAABIAAAANAAAAAwEAAAAHAAAABAAAABsAAAANAAAAKAAAAA0AAAArAAAADQAAAC4AAAANAAAAMQAAAAcAAAAEAAAAGwAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAGwAAAA0AAAApAAAADQAAACwAAAANAAAALwAAAA0AAAAyAAAABwAAAAQAAAAbAAAADQAAACoAAAANAAAALQAAAA0AAAAwAAAADQAAADMAAAASAAAADQAAAAMBAAAABwAAAAQAAAAcAAAADQAAACgAAAANAAAAKwAAAA0AAAAuAAAADQAAADEAAAAHAAAABAAAABwAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAABIAAAANAAAAAwEAAAAHAAAABAAAABwAAAANAAAAKQAAAA0AAAAsAAAADQAAAC8AAAANAAAAMgAAAAcAAAAEAAAAHAAAAA0AAAAqAAAADQAAAC0AAAANAAAAMAAAAA0AAAAzAAAAEgAAAA0AAAADAQAAAAcAAAAEAAAAHQAAAA0AAAAoAAAADQAAACsAAAANAAAALgAAAA0AAAAxAAAABwAAAAQAAAAdAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAASAAAADQAAAAMBAAAABwAAAAQAAAAdAAAADQAAACkAAAANAAAALAAAAA0AAAAvAAAADQAAADIAAAAHAAAABAAAAB0AAAANAAAAKgAAAA0AAAAtAAAADQAAADAAAAANAAAAMwAAAAIA#####wAEZWdhbAADeD0wAAAAAwgAAAAEAAAAAAAAAAEAAAAAAAAAAAAAAAQAAXgAAXkAAXoAAXT#####AAAAAQAMQ1Rlc3RFcU5hdE9wAP####8AB2VnYWxlcTEAAAABAAAAOAAAABMA#####wAHZWdhbGVxMgAAAAEAAAA4AAAAEwD#####AAdlZ2FsZXEzAAAAAQAAADgAAAATAP####8AB2VnYWxlcTQAAAAEAAAAOAAAAAwA#####wAHc29sZnJhYwAHZnJhYyhYKQAAAAYZAAAADQAAACMAAAAOAP####8AA254MAAMc29sZnJhYygxLDEpAAAADwAAAD0AAAABP#AAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AA2R4MAAMc29sZnJhYygxLDIpAAAADwAAAD0AAAABP#AAAAAAAAAAAAABQAAAAAAAAAAAAAAOAP####8AA255MAAMc29sZnJhYygyLDEpAAAADwAAAD0AAAABQAAAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AA2R5MAAMc29sZnJhYygyLDIpAAAADwAAAD0AAAABQAAAAAAAAAAAAAABQAAAAAAAAAAAAAAOAP####8AA256MAAMc29sZnJhYygzLDEpAAAADwAAAD0AAAABQAgAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AA2R6MAAMc29sZnJhYygzLDIpAAAADwAAAD0AAAABQAgAAAAAAAAAAAABQAAAAAAAAAAAAAAOAP####8AA250MAAMc29sZnJhYyg0LDEpAAAADwAAAD0AAAABQBAAAAAAAAAAAAABP#AAAAAAAAAAAAAOAP####8AA2R0MAAMc29sZnJhYyg0LDIpAAAADwAAAD0AAAABQBAAAAAAAAAAAAABQAAAAAAAAAAAAAAOAP####8AB2NvcnJlY3QAM2RlZzEmZGVnMiZkZWczJmRlZzQmZWdhbGVxMSZlZ2FsZXEyJmVnYWxlcTMmZWdhbGVxNAAAAAMKAAAAAwoAAAADCgAAAAMKAAAAAwoAAAADCgAAAAMKAAAADQAAADQAAAANAAAANQAAAA0AAAA2AAAADQAAADcAAAANAAAAOQAAAA0AAAA6AAAADQAAADsAAAANAAAAPAAAAA4A#####wAGdW5lc29sAAdkZXRBPD4wAAAAAwkAAAANAAAAIQAAAAEAAAAAAAAAAAAAAAgA#####wAGemVybzE0AA9hYnMoeCk8MTBeKC0xNCkAAAADBAAAAAYAAAAABAAAAAAAAAARAAAAAUAkAAAAAAAAAAAAEAAAAAFALAAAAAAAAAABeAAAAA4A#####wAFZXhhY3QAS3plcm8xNChueDAvZHgwLXgwKSZ6ZXJvMTQobnkwL2R5MC15MCkmemVybzE0KG56MC9kejAtejApJnplcm8xNChudDAvZHQwLXQwKQAAAAMKAAAAAwoAAAADCgAAABIAAABIAAAAAwEAAAADAwAAAA0AAAA+AAAADQAAAD8AAAANAAAAJAAAABIAAABIAAAAAwEAAAADAwAAAA0AAABAAAAADQAAAEEAAAANAAAAJQAAABIAAABIAAAAAwEAAAADAwAAAA0AAABCAAAADQAAAEMAAAANAAAAJgAAABIAAABIAAAAAwEAAAADAwAAAA0AAABEAAAADQAAAEUAAAANAAAAJ#####8AAAACAAZDTGF0ZXgA#####wAAAP8BAAD#####E0AeAAAAAAAAQGsQo9cKPXEBAe#v+wAAAAAAAAAAAAAAAQAAAAAAAAAAAhZcSWZ7Y29ycmVjdH0KewpcSWZ7dW5lc29sfQp7ClxiZWdpbnthcnJheX17bH0KXHRleHR7TGUgc3lzdMOobWUgYWRtZXQgdW4gdW5pcXVlIHF1YWRydXBsZXQgKCR4JDskeSQ7JHokLCR0JCkgc29sdXRpb24gfSAKXFwgXGxlZnQoIFxiZWdpbnthcnJheX17bH0geCBcXCB5XFwgeiBcXCB0IFxlbmR7YXJyYXl9IFxyaWdodClcYXBwcm94IFxsZWZ0KCBcVmFse1gsMTJ9IFxyaWdodCkKXFwgXHRleHR7U29sdXRpb24gcmF0aW9ubmVsbGUgXElme2V4YWN0fXt9e2FwcHJvY2jDqWUgOiB9fQpcbGVmdCggXGJlZ2lue2FycmF5fXtsfSB4IFxcIHlcXCB6IFxcIHQgXGVuZHthcnJheX0gXHJpZ2h0KSBcSWYge2V4YWN0fXs9fXtcYXBwcm94fSBcbGVmdCggXFZhbEZyYWN7WH0gXHJpZ2h0KQpcZW5ke2FycmF5fQp9CnsKXHRleHRjb2xvcntyZWR9e1x0ZXh0e0xlIHN5c3TDqG1lIG4nYSBwYXMgdW5lIHNldWxlIHNvbHV0aW9ufX0KfQoKfQp7Clx0ZXh0Y29sb3J7cmVkfXtcdGV4dHtTeXN0w6htZSBpbmNvcnJlY3Qgb3Ugbm9uIGxpbsOpYWlyZX19Cn3###############8=Inicie MathGraph32 (versión 6.8.0 o posterior) y use el icono  para crear una figura sin referencial y sin unidad de longitud.
para crear una figura sin referencial y sin unidad de longitud.
Nuestras cuatro ecuaciones estarán contenidas en funciones de cuatro variables (funcionalidad disponible solo desde la versión 6.8.0).
Desplegando la barra de herramientas de cálculos, haga clic con el botón derecho en el icono  y elija Función real de tres o más variables.
y elija Función real de tres o más variables.
Se abre un cuadro de diálogo. Llénelo como se muestra a continuación :
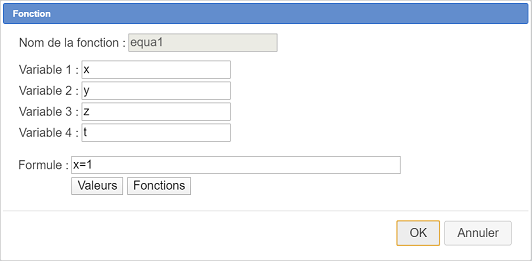
Haga lo mismo para crear otras tres funciones de variables x, y, z y t con las fórmulas siguientes :
| Nombre de la función | Fórmula |
| equa2 | x+y=2 |
| equa3 | x+y+z=3 |
| equa4 | x+y+z=4-t |
Posteriormente podemos modificar estas ecuaciones pero aquí sabemos que nuestro sistema admite solo una solución $(x ;y ;z ;t)=(1 ;1 ;1 ;1)$
Ahora asociemos estas cuatro funciones con editores de fórmulas que luego nos permitirán modificar el sistema a resolver.
Abra la barra de visualización y haga clic en el icono  .
.
Haga clic en en la parte superior izquierda de la figura y luego complete el cuadro de diálogo como se muestra a continuación :
Haga lo mismo para crear otros 3 editores de fórmulas asociados con las funciones equa2, equa3, equa4 alineándolos debajo del anterior. Para mover un editor, captúrelo con la herramienta  (la parte activa para capturar es el título).
(la parte activa para capturar es el título).
Cree de nuevo cuatro funciones más de variables x, y, z y t con las fórmulas siguientes
| Nombre de la función | Fórmula |
| df1 | gauche(equa1(x,y,z,t))-droit(equa1(x,y,z,t)) |
| df2 | gauche(equa2(x,y,z,t))-droit(equa2(x,y,z,t)) |
| df3 | gauche(equa3(x,y,z,t))-droit(equa3(x,y,z,t)) |
| df4 | gauche(equa4(x,y,z,t))-droit(equa4(x,y,z,t)) |
Los operadores izquierdo y derecho se utilizan para aislar la parte izquierda y derecha del operador de un cálculo (aquí el operador será una igualdad).
Vuelva a desarrollar la barra de herramientas de cálculos, haga clic con el botón derecho en el icono  y seleccione Derivada parcial.
y seleccione Derivada parcial.
La primera derivada parcia a crear es la de equa1 con respecto a la variable x.
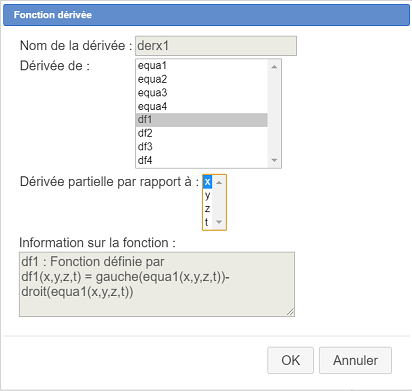
Aquí están las 16 derivadas parciales a crear como se muestra a continuación :
| Nombre de la derivada parcial | Derivada de | Variable de derivación |
| derx1 | df1 | x |
| dery1 | df1 | y |
| derz1 | df1 | z |
| dert1 | df1 | t |
| derx2 | df2 | x |
| dery2 | df2 | y |
| derz2 | df2 | z |
| dert2 | df2 | t |
| derx3 | df3 | x |
| dery3 | df3 | y |
| derz3 | df3 | z |
| dert3 | df3 | t |
| derx4 | df4 | x |
| dery4 | df4 | y |
| derz4 | df4 | z |
| dert4 | df4 | t |
Ahora crearemos una matriz A de cuatro filas y cuatro columnas.
Para esto, despleguemos la barra de herramientas de cálculo nuevamente, hacemos clic derecho en el ícono  y elegimos Matriz.
y elegimos Matriz.
Completamos el cuadro de diálogo como se muestra a continuación :
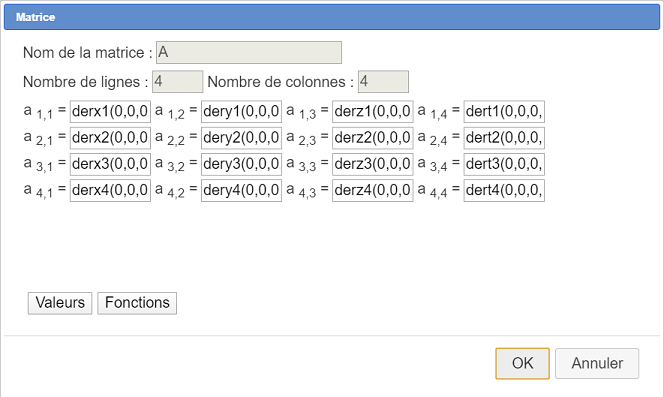
La primera fórmula es por ejemplo : derx1(0,0,0,0) puesto que derx1 es una función de 4 variables ya que es una derivada parcial de una función de 4 variables con respecto a x.
Aquí están las 16 fórmulas para los 16 elementos de la matriz :
| Elemento | Fórmula |
| $a_{11}$ | derx1(0,0,0,0) |
| $a_{12}$ | dery1(0,0,0,0) |
| $a_{13}$ | derz1(0,0,0,0) |
| $a_{14}$ | dert1(0,0,0,0) |
| $a_{21}$ | derx2(0,0,0,0) |
| $a_{22}$ | dery2(0,0,0,0) |
| $a_{23}$ | derz2(0,0,0,0) |
| $a_{24}$ | dert2(0,0,0,0) |
| $a_{31}$ | derx3(0,0,0,0) |
| $a_{32}$ | dery3(0,0,0,0) |
| $a_{33}$ | derz3(0,0,0,0) |
| $a_{34}$ | dert3(0,0,0,0) |
| $a_{41}$ | derx4(0,0,0,0) |
| $a_{42}$ | dery4(0,0,0,0) |
| $a_{43}$ | derz4(0,0,0,0) |
| $a_{44}$ | dert4(0,0,0,0) |
Procedemos de la misma manera para crear una matriz real B con 3 filas y una columna como se muestra a continuación :
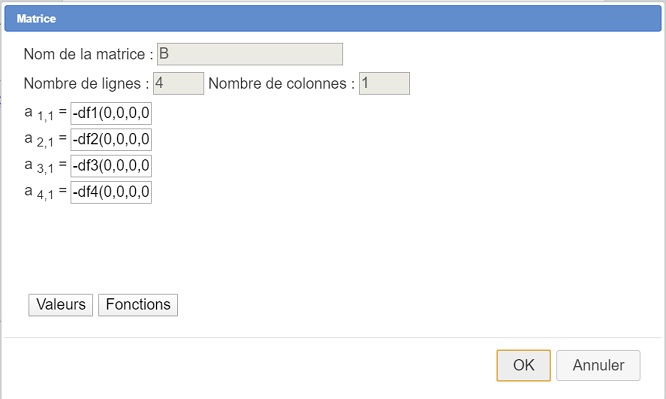
Aquí están las 4 fórmulas para los 16 elementos de la matriz :
| Elemento | Fórmula |
| $b_{11}$ | -df1(0,0,0,0) |
| $b_{21}$ | -df2(0,0,0,0) |
| $b_{31}$ | -df3(0,0,0,0) |
| $b_{41}$ | -d4(0,0,0,0) |
Ahora vamos a pedir el cálculo del determinante de la matriz A que nos permitirá saber si el sistema admite o no una solución única.
Volvamos a desplegar la barra de herramientas de cálculo, hacemos clic con el botón derecho en el icono  y elegimos Determinante.
y elegimos Determinante.
Completamos el cuadro de diálogo como se muestra a continuación :
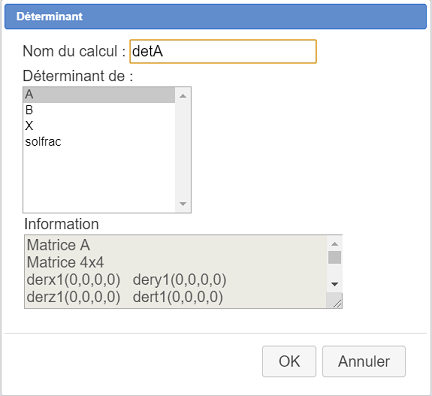
Ahora vamos a crear un cálculo matricial llamado X que contiene la solución de este sistema (cuando esta es única).
Volvamos a desplegar la barra de herramientas de cálculo, hacemos clic con el botón derecho en el icono  y elegimos Cálculo matricial.
y elegimos Cálculo matricial.
Completamos el cuadro de diálogo como se muestra a continuación :
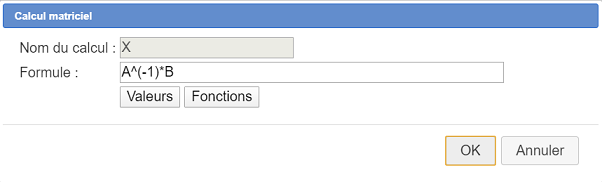
Utilizamos el icono siguiente  para crear los cálculos reales siguientes :
para crear los cálculos reales siguientes :
| Nombre del cálculo | Fórmula | Comentario |
| x0 | X(1,1) | Contiene el valor x de la solución única |
| y0 | X(2,1) | Contiene el valor y de la solución única |
| z0 | X(3,1) | Contiene el valor z de la solución única |
| t0 | X(4,1) | Contiene el valor t de la solución única |
| x1 | 1+rand(0) | Valor aleatorio utilizado para verificar que las derivadas parciales son constantes |
| x2 | 1+rand(0) | |
| x3 | 1+rand(0) | |
| y1 | 1.1+rand(0) | |
| y2 | 1.1+rand(0) | |
| y3 | 1.1+rand(0) | |
| z1 | 1.2+rand(0) | |
| z2 | 1.2+rand(0) | |
| z3 | 1.2+rand(0) | |
| t1 | 1.3+rand(0) | |
| t2 | 1.3+rand(0) | |
| t3 | 1.3+rand(0) |
Ahora creamos cuatro cálculos reales llamados deg1, deg2, deg3 y deg4 con las fórmulas siguientes :
Para deg1 :
zero(derx1(x1,y1,z1,t1)-derx1(x2,y2,z2,t2))&zero(derx1(x2,y2,z2,t2)-derx1(x3,y3,z3,t3))&zero(dery1(x1,y1,z1,t1)-dery1(x2,y2,z2,t2))&zero(dery1(x2,y2,z2,t2)-dery1(x3,y3,z3,t3))&zero(derz1(x1,y1,z1,t1)-derz1(x2,y2,z2,t2))&zero(derz1(x2,y2,z2,t2)-derz1(x3,y3,z3,t3))&zero(dert1(x1,y1,z1,t1)-dert1(x2,y2,z2,t2))&zero(dert1(x2,y2,z2,t2)-dert1(x3,y3,z3,t3))Para deg2 :
zero(derx2(x1,y1,z1,t1)-derx2(x2,y2,z2,t2))&zero(derx2(x2,y2,z2,t2)-derx2(x3,y3,z3,t3))&zero(dery2(x1,y1,z1,t1)-dery2(x2,y2,z2,t2))&zero(dery2(x2,y2,z2,t2)-dery2(x3,y3,z3,t3))&zero(derz2(x1,y1,z1,t1)-derz2(x2,y2,z2,t2))&zero(derz2(x2,y2,z2,t2)-derz2(x3,y3,z3,t3))&zero(dert2(x1,y1,z1,t1)-dert2(x2,y2,z2,t2))&zero(dert2(x2,y2,z2,t2)-dert2(x3,y3,z3,t3))Para deg3 :
zero(derx3(x1,y1,z1,t1)-derx3(x2,y2,z2,t2))&zero(derx3(x2,y2,z2,t2)-derx3(x3,y3,z3,t3))&zero(dery3(x1,y1,z1,t1)-dery3(x2,y2,z2,t2))&zero(dery3(x2,y2,z2,t2)-dery3(x3,y3,z3,t3))&zero(derz3(x1,y1,z1,t1)-derz3(x2,y2,z2,t2))&zero(derz3(x2,y2,z2,t2)-derz3(x3,y3,z3,t3))&zero(dert3(x1,y1,z1,t1)-dert3(x2,y2,z2,t2))&zero(dert3(x2,y2,z2,t2)-dert3(x3,y3,z3,t3))Para deg4 :
zero(derx4(x1,y1,z1,t1)-derx4(x2,y2,z2,t2))&zero(derx4(x2,y2,z2,t2)-derx4(x3,y3,z3,t3))&zero(dery4(x1,y1,z1,t1)-dery4(x2,y2,z2,t2))&zero(dery4(x2,y2,z2,t2)-dery4(x3,y3,z3,t3))&zero(derz4(x1,y1,z1,t1)-derz4(x2,y2,z2,t2))&zero(derz4(x2,y2,z2,t2)-derz4(x3,y3,z3,t3))&zero(dert4(x1,y1,z1,t1)-dert4(x2,y2,z2,t2))&zero(dert4(x2,y2,z2,t2)-dert4(x3,y3,z3,t3))Por ejemplo, deg1 valdrá 1 si la ecuación contenida en equa1 es efectivamente de primer grado con respecto a las variables x, y, z y t.
También debemos probar si las fórmulas contenidas en las cuatro funciones equa1, equa2, equa3 y equa4 son de hecho igualdades.
Para eso definiremos una función real de cuatro variables llamada igual cuya fórmula es una igualdad.
Creamos entonces una función de cuatro variables llamada igual con la fórmula x=0 (cualquier función está bien siempre que incluya una igualdad).
Volvemos a desplegar la barra de herramientas de cálculo, hacemos clic con el botón derecho en el icono  y seleccionamos Test de equivalencia de tipo de operador..
y seleccionamos Test de equivalencia de tipo de operador..
Creamos el primer test nominado egaleq1 como se muestra a continuación :
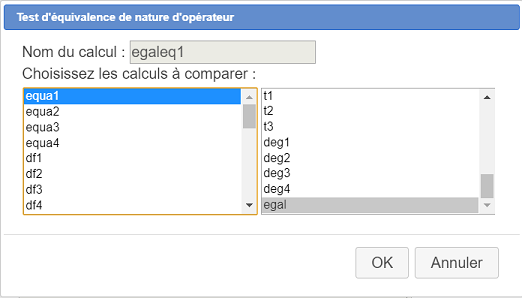
Luego creamos de la misma manera otros tres tests de equivalencia de la naturaleza del operador :
| Nombre del test de naturaleza de operador | Test entre |
| egaleq2 | equa2 et egal |
| egaleq3 | equa3 et egal |
| egaleq4 | equa4 et egal |
Ahora vamos a crear soluciones racionales aproximadas para los cuatro miembros de nuestra solución (que solo existe si es única).
Para esto usaremos un cálculo matricial.
Desde que se introdujo el cálculo matricial en MathGraph32, se ha agregado una nueva función frac que se puede usar en los cálculos.
Se puede aplicar a un número, una matriz columna o una matriz de fila.
Aplicado a una matriz columna de n filas, devuelve una matriz de n filas y dos columnas. La primera columna del resultado devuelve los numeradores de los valores racionales aproximados de la matriz inicial (con error menor a 10 ^ -12) y la segunda columna los denominadores.
Volvemos a desplegar la barra de herramientas de cálculo, hacemos clic con el botón derecho en el icono  y elegimos Cálculo matricial.
y elegimos Cálculo matricial.
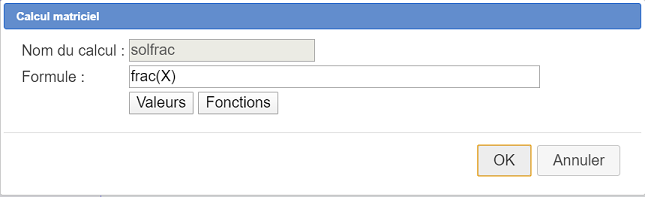
Creamos un cálculo de matricial llamado solfrac como se muestra a continuación :

La fórmula a utilizar es : frac (X)
Ahora recuperaremos los numeradores y denominadores de estas fracciones racionales aproximadas en los cálculos reales.
Creamos los siguientes cálculos reales (herramienta  ) :
) :
| Nombre del cálculo | Fórmula |
| nx0 | solfrac(1,1) |
| dx0 | solfrac(1,2) |
| ny0 | solfrac(2,1) |
| dx0 | solfrac(2,2) |
| nz0 | solfrac(3,1) |
| dz0 | solfrac(3,2) |
| nt0 | solfrac(4,1) |
| dt0 | solfrac(4,2) |
| correct | deg1°2°3°4&egaleq1&egaleq2&egaleq3&egaleq4 |
El último cálculo correcto tomará el valor 1 si el sistema ingresado es efectivamente de grado 1 e incluye efectivamente una igualdad en cada editor y 0 en caso contrario.
Creamos con el icono  un cálculo real llamado unesol con la siguiente fórmula :
un cálculo real llamado unesol con la siguiente fórmula :
detA<>0
unesol valdrá 1 si el sistema admite una solución única.
Ahora usamos el icono  para crear una función real de la variable x denominada zero14 definida por la siguiente fórmula :
para crear una función real de la variable x denominada zero14 definida por la siguiente fórmula :
abs(x)<10^(-14)
Nuestra solución racional aproximada está dada dentro de 10^(-12) aproximada.
Si la diferencia entre ésta y nuestra solución aproximada contenida en (x0, y0, z0, t0) es menor que 10 ^ (- 14) consideraremos que la solución racional aproximada es exacta.
Usaremos el ícono  para crear un cálculo real denominado exacto con la siguiente fórmula :
para crear un cálculo real denominado exacto con la siguiente fórmula :
zero14(nx0/dx0-x0)&zero14(ny0/dy0-y0)&zero14(nz0/dz0-z0)&zero14(nt0/dt0-t0)
Todavía tenemos que crear una pantalla LaTeX responsable de mostrar la solución cuando es única, de lo contrario se mostrará información si no es única o si el sistema no es lineal.
En la barra de herramientas de visualizaciones, use el icono  .
.
Hagamos clic debajo de los editores de fórmulas para designar la ubicación de la visualización LaTeX.
Utilizamos el siguiente código LaTeX :
Esta visualización LaTeX tiene códigos de visualización condicionales \ If específicos de MathGraph32.
Recordemos que la sintaxis es \ If \condición \ \ código LaTeX si la condición es igual a 1 \ \ código LaTeX en caso contrario \
El código
\Val {X, 12 \ hace que se muestre la matriz X, cada término redondeado a 12 lugares decimales.
El código \ ValFrac \ X \ hace que se muestre la matriz X donde cada término se escribe como una fracción racional aproximada dentro de 10 ^ (- 12).
Ahora podemos modificar los editores de fórmulas para resolver el sistema de su elección.
Si, por ejemplo, ingresamos x² = 1 como la primera ecuación, el sistema se declarará no lineal.
Si ingresamos como la primera ecuación 3x = 1 sin cambiar las otras ecuaciones, veremos que la solución racional (1/3 ; 5/3 ; 1 ; 1) se declara como exacta.
Pero si ponemos como primera ecuación la fórmula 3x = 1.0000000000001, la misma solución se declara como aproximada.