Toutes les versions de cet article : [English] [Español] [français]
Este artículo ha sido adaptado a la versión JavaScript de MathGraph32.
MathGraph32 hace posible crear sucesiones del tipo $u_{n+1}=f(u_n)$ y representarlas gráficamente.
Este artículo estudia las sucesiones recurrentes complejas de la forma $u_{n + 1} = f\left( {u_n } \right)$ con $f(z) = \frac{1}{2}(z + \frac{a}{z})$.
Se generaliza así el algoritmo de Babilonia para calcular una raíz cuadrada en el conjunto de los números complejos.
El artículo muestra cómo MathGraph32 hace que sea muy fácil visualizar resultados interesantes con figuras animadas en línea por MathGraph32.
Haga clic aquí para leer este artículo.
Cree una nueva figura usando el ícono  y elije un referencial ortonormal con vectores.
y elije un referencial ortonormal con vectores.
Usando el icono  cree un punto libre y asígnele el nombre M.
cree un punto libre y asígnele el nombre M.
Expanda la barra de herramientas de medición y use el ícono  para medir el afijo del punto M (simplemente haga clic en M). Se abre un cuadro de diálogo para elegir el nombre de esta medida. Introduzca, por ejemplo, zM.
para medir el afijo del punto M (simplemente haga clic en M). Se abre un cuadro de diálogo para elegir el nombre de esta medida. Introduzca, por ejemplo, zM.
Expanda la barra de herramientas de cálculos y use el ícono 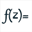 para crear una función compleja f de variable compleja nominada t y definida por la fórmula f( t)=t+1/t^2.
para crear una función compleja f de variable compleja nominada t y definida por la fórmula f( t)=t+1/t^2.
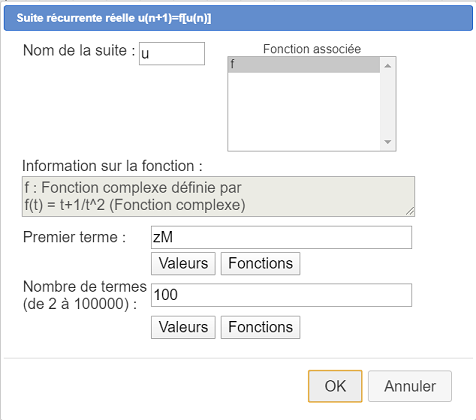
Creamos ahora una sucesión recurrente compleja llamada u del tipo u(n+1)=f[u(n)] cuyo primer término será el afijo que acabamos de medir.
Para ello, en la barra de herramientas de cálculos, utilice el icono 
Se abre un cuadro de diálogo.
Introduzca u en el campo Nombre.
La función f ya está seleccionada.
Utilice el botón Valores para elegir zM, que representa el afijo de M en el campo Primer término.
En el campo Número de términos ingrese 100.
Valide con OK.
Aquí está la caja de diálogo antes de la validación :
Vamos a crear ahora la gráfica de esta sucesión.
Active el color azul y el estilo de línea punteada.
Luego use el ícono  (gráfico de una sucesión recurrente compleja).
(gráfico de una sucesión recurrente compleja).
Se abre un cuadro de diálogo como este :
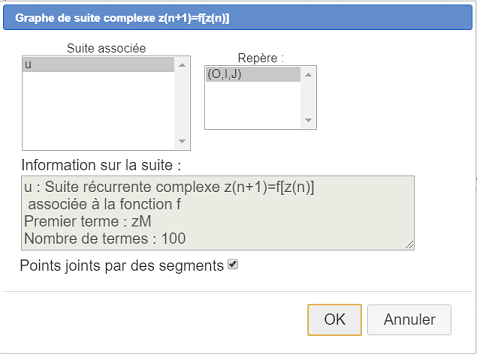
La sucesión u ya está seleccionada. Valide las opciones predeterminadas.
Ahora vamos a crear un editor de fórmulas que nos permitirá modificar la fórmula de f(t) directamente en la figura.
Al expandir la barra de herramientas de cálculo, utilice el icono  y haga clic en la parte superior izquierda de la figura (no demasiado a la izquierda).
y haga clic en la parte superior izquierda de la figura (no demasiado a la izquierda).
Se abre un cuadro de diálogo. Rellénelo como a continuación (tenga cuidado de asignar el editor a la función compleja f)
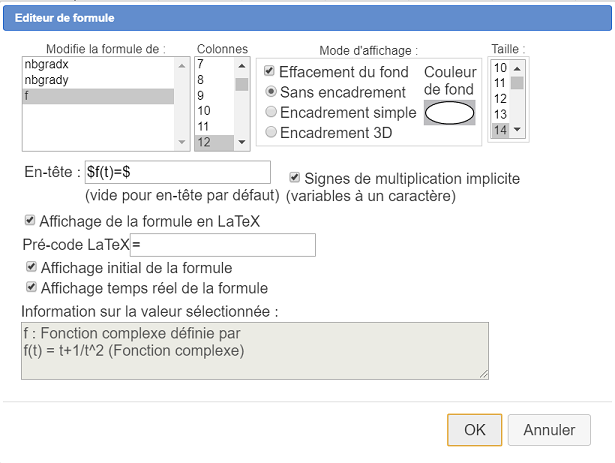
Finalmente, mostraremos los términos de esta sucesión en la figura.
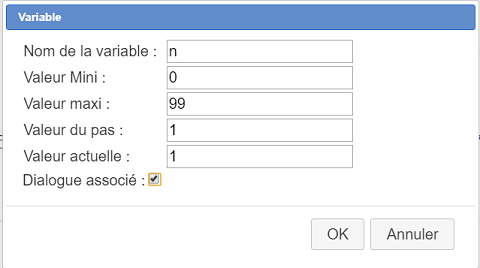
Para ello vamos a utilizar una variable cuyos valores enteros oscilarán entre 0 y 99 (hemos elegido 100 términos para la sucesión y los índices empiezan en 0).
Use el ícono  y complete el cuadro de diálogo como se muestra a continuación (las variables siempre se insertan en la parte superior de la lista de objetos creados). No olvide marcar la casilla Diálogo asociado.
y complete el cuadro de diálogo como se muestra a continuación (las variables siempre se insertan en la parte superior de la lista de objetos creados). No olvide marcar la casilla Diálogo asociado.
.
Expanda la barra de herramientas de cálculos y use el ícono  para crear un cálculo complejo llamado un con la fórmula f(n).
para crear un cálculo complejo llamado un con la fórmula f(n).
Ahora usemos una pantalla LaTeX dinámica.
Expanda la barra de herramientas de visualizaciones y use el icono  para crear una visualización LaTeX libre y haga clic en la parte superior izquierda de la figura, debajo del editor de fórmulas. Rellene el cuadro de diálogo como se muestra a continuación. Puede usar el botón Insertar valor para insertar el código LaTeX especial que muestre los valores de n y un (para un debe solicitar 12 decimales).
para crear una visualización LaTeX libre y haga clic en la parte superior izquierda de la figura, debajo del editor de fórmulas. Rellene el cuadro de diálogo como se muestra a continuación. Puede usar el botón Insertar valor para insertar el código LaTeX especial que muestre los valores de n y un (para un debe solicitar 12 decimales).
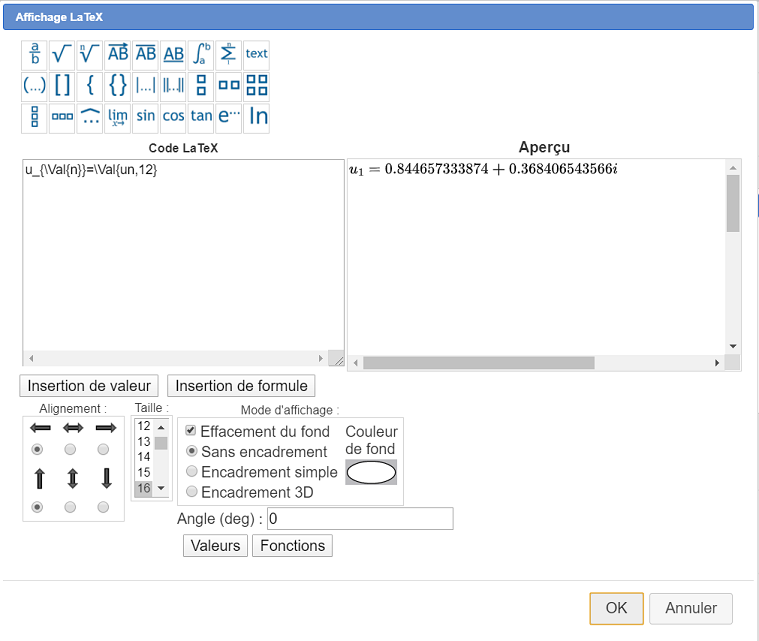
Aquí está el código LaTeX a usar :
La figura está lista.
Ahora puede variar los valores de n haciendo clic en la parte inferior derecha de la figura con los botones + y -.
Puede verlo a continuación impulsado por el motor JavaScript de MathGraph32.
Puede capturar el punto M.
Cambie, por ejemplo, la fórmula de f(t) por :
y capture M : la secuencia converge hacia 2i o hacia -2i (sucesión compleja de Babilonia).