Toutes les versions de cet article : [English] [Español] [français]
Cet exemple nécessite une grande puissance de calcul mais le moteur de calcul de MathGraph32 est suffisamment performant pour ça.
Vous pouvez voir ci-dessous la figure en action. Cliquez sur la macro Animer la roue pour lancer l’animation.
Démarrez MathGraph32 (version JavaScript) et utilisez l’icône  pour créer une figure munie d’un repère orthonormal.
pour créer une figure munie d’un repère orthonormal.
Utilisez l’icône  (options de la figure) et vérifiez que la case radian est bien cochée pour l’unité d’angle.
(options de la figure) et vérifiez que la case radian est bien cochée pour l’unité d’angle.
En déroulant la barre d’outils des calculs (troisième barre d’outils à partir du bas), utilisez maintenant l’icône  et créez une fonction f comme ci-dessous. Laissez cochée la case Tracer courbe.
et créez une fonction f comme ci-dessous. Laissez cochée la case Tracer courbe.
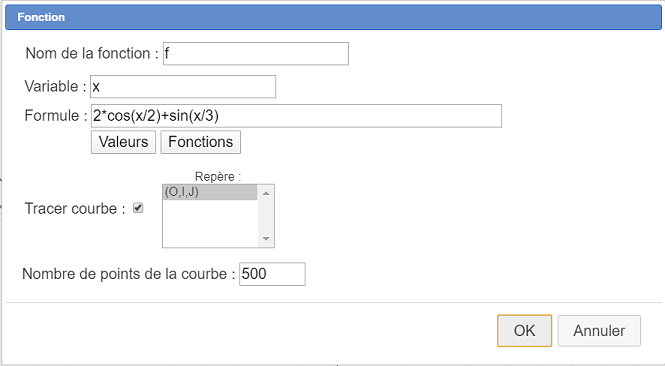
Nous allons maintenant demander à MathGraph32 de calculer la dérivée formelle de la fonction f.
Utilisez pour cela l’icône  . Dans la boîte de dialogue qui s’ouvre, la fonction f est déjà sélectionnée. Nommez cette dérivée f ’ et validez.
. Dans la boîte de dialogue qui s’ouvre, la fonction f est déjà sélectionnée. Nommez cette dérivée f ’ et validez.
Un petit rappel préliminaire : La longueur (algébrique) de l’arc de courbe de f entre les abscisses 0 et a est donné par la formule $ \int_{0}^{a} \sqrt{1+(f’(x))^2}dx $ (avec f dérivable à dérivée continue).
Utilisez l’icône  pour créer une fonction g comme ci-dessous, en décochant la case Tracer courbe (cette fonction nous servira à calculer des longueurs approchées d’arcs de courbe).
pour créer une fonction g comme ci-dessous, en décochant la case Tracer courbe (cette fonction nous servira à calculer des longueurs approchées d’arcs de courbe).
Voici la formule à entrer pour g(x) : integrale(sqrt(1+f'(t)^2),t,0,x)
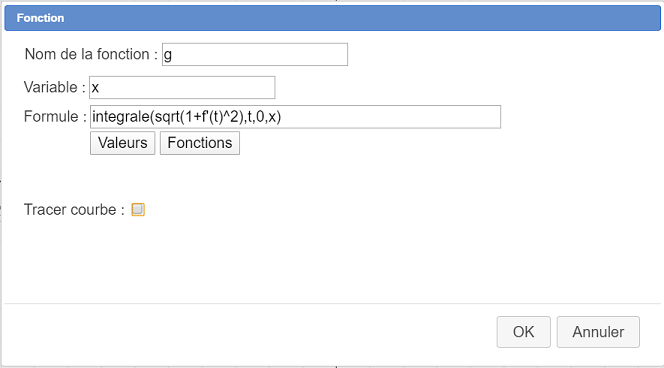
A noter qu’en cliquant sur le bouton Fonctions on vous propose une liste des fonctions prédéfinies avec leur syntaxe. Ici le premier paramètre de la fonction prédéfinie intégrale est la formule à intégrer, le second la variable formelle utilisée pour la fonction à intégrer (ici t), le troisième est la borne inférieure d’intégration et le dernier la borne supérieure d’intégration.
g(x) représentera donc la longueur algébrique de l’arc de courbe de f entre les abscisses 0 et x.
Utilisez maintenant l’icône  pour créer deux calculs réels comme expliqué ci-dessous :
pour créer deux calculs réels comme expliqué ci-dessous :
| Nom du calcul | Formule | Explications |
| L | g(16) | L représentera la longueur algébrique de l’arc de courbe de f entre les abscisses 0 et 16 . Il est positif. |
| L’ | g(-16) | L’ représentera la longueur algébrique de l’arc de courbe de f entre les abscisses 0 et -16 . Il est négatif. |
Nous allons maintenant créer un curseur dont la valeurs iront de L’ à L.
Pour cela activez l’icône  dans la barre d’outils des calculs ; cliquez en haut et à gauche de la figure.
dans la barre d’outils des calculs ; cliquez en haut et à gauche de la figure.
Remplissez la boîte de dialogue comme ci-dessous :
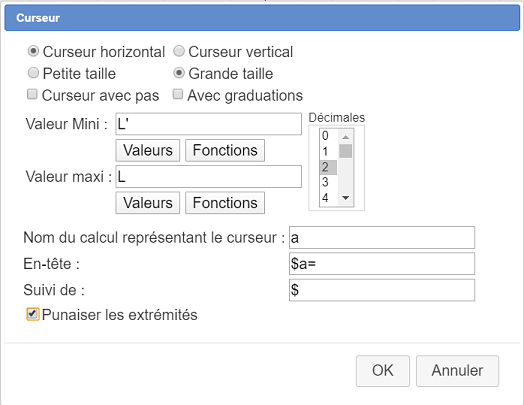
Ici on demande un curseur de grande taille à valeurs non entières. Les $ servent à ce que l’en-tête soit affichée en mode LaTeX.
La valeur de a représentera la valeur algébrique de la longueur parcourue par la roue.
Pour chaque valeur de a nous avons besoin de connaître l’abscisse x de la courbe pour laquelle on a parcouru cette longueur.
Nous allons calculer x comme valeur approchée d’une solution d’équation.
Utilisez pour cela l’icône  et remplissez la boîte de dialogue comme ci-dessous :
et remplissez la boîte de dialogue comme ci-dessous :
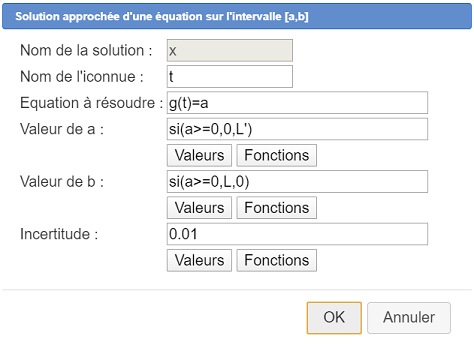
L’équation à résoudre est g(t)=a (d’inconnue t) et nous demandons la solution de cette équation sur l’intervalle [0 ; L] si a est positif et [L’ ; 0] si a est négatif (plus l’intervalle de recherche est restreint plus les calculs seront rapides). Pour cela nous utilisons un si dans les formules des bornes inférieures et supérieures de l’intervalle de recherche.
Le calcul de x est gourmand en puissance de calcul car chaque calcul de x se fait par dichotomie pour approcher la solution et, de plus, la fonction g utilisée utilise un calcul approché d’intégrale.
Il est maintenant temps de créer la "roue" qui va tourner sur la courbe.
Créons d’abord une variable r qui représentera la rayon de cette roue.
Utilisez l’icône  pour créer une variable nommée r avec comme valeur mini 0.25, valeur maxi 1.5, pas d’incrémentation 0.25 et valeur actuelle 1. Cochez la case dialogue associé. Un élément graphique en bas et à droite de la figure permettra de faire varier r en cliquant sur les boutons + et -.
pour créer une variable nommée r avec comme valeur mini 0.25, valeur maxi 1.5, pas d’incrémentation 0.25 et valeur actuelle 1. Cochez la case dialogue associé. Un élément graphique en bas et à droite de la figure permettra de faire varier r en cliquant sur les boutons + et -.
Dans la palette des couleurs, activez la couleur marron.
Utilisez l’icône  et demandez le point de coordonnées (x ; 0).
et demandez le point de coordonnées (x ; 0).
En déroulant la barre des affichages, utilisez l’icône  pour créer un affichage LaTex lié au dernier point créé avec comme code LaTeX x et demandez un affichage centré horizontalement et au-dessous du point. Vous pouvez ensuite capturer cet affichage avec l’outil
pour créer un affichage LaTex lié au dernier point créé avec comme code LaTeX x et demandez un affichage centré horizontalement et au-dessous du point. Vous pouvez ensuite capturer cet affichage avec l’outil  pour le descendre légèrement. La création de cet affichage LaTeX n’est pas indispensable pour la suite.
pour le descendre légèrement. La création de cet affichage LaTeX n’est pas indispensable pour la suite.
Utilisez de nouveau l’icône  et demandez le point de coordonnées (x ; f(x)) qui est donc le point de la courbe d’abscisse x.
et demandez le point de coordonnées (x ; f(x)) qui est donc le point de la courbe d’abscisse x.
Activez le style de trait pointillé et utilisez l’icône  pour joindre par un segment les points de coordonnées (x ; 0) et (x ; f(x))
pour joindre par un segment les points de coordonnées (x ; 0) et (x ; f(x))
Nous allons maintenant tracer la tangente à la courbe en ce dernier point.
Pour cela utilisez l’icône  , cliquez sur le dernier point créé et, dans la boîte de dialogue qui s’ouvre, entrez comme coefficient directeur : f ’(x).
, cliquez sur le dernier point créé et, dans la boîte de dialogue qui s’ouvre, entrez comme coefficient directeur : f ’(x).
Utilisez maintenant l’outil  pour créer la perpendiculaire à cette tangente passant par le point de la courbe : cliquez en premier sur la tangente puis sur le point de coordonnées (x ;f (x)). Cette perpendiculaire est la normale à la courbe en ce point.
pour créer la perpendiculaire à cette tangente passant par le point de la courbe : cliquez en premier sur la tangente puis sur le point de coordonnées (x ;f (x)). Cette perpendiculaire est la normale à la courbe en ce point.
Utilisez l’icône  pour créer le cercle de centre le point de coordonnées (x ; f(x)) et rayon r (où r est la variable précédemment définie).
pour créer le cercle de centre le point de coordonnées (x ; f(x)) et rayon r (où r est la variable précédemment définie).
Utilisez l’outil  pour créer l’intersection de ce cercle avec la normale à la courbe (il suffit de cliquer à l’intersection quand est affiché cette intersection près du pointeur souris).
pour créer l’intersection de ce cercle avec la normale à la courbe (il suffit de cliquer à l’intersection quand est affiché cette intersection près du pointeur souris).
Deux points d’intersection apparaissent. Nous n’utiliserons que celui qui est situé au-dessus de la tangente. Nous l’appellerons A.
Nous allons créer la roue. Dans la palette des couleurs, activez la couleur bleue et choisissez un style de trait continu de deux pixels d’épaisseur.
Utilisez l’outil  pour créer le cercle de centre A et passant par le point de la courbe. Ce cercle sera notre "roue".
pour créer le cercle de centre A et passant par le point de la courbe. Ce cercle sera notre "roue".
Utilisez maintenant l’outil  de la barre d’outils supérieure pour masquer : le premier cercle, le deuxième point d’intersection, les deux droites (tangente et normale).
de la barre d’outils supérieure pour masquer : le premier cercle, le deuxième point d’intersection, les deux droites (tangente et normale).
Nous allons maintenant créer des rayons pour cette roue.
Dans la palette des couleurs activez la couleur rouge et activez le style de trait pointillé.
Déroulez la barre d’outils des transformations et utilisez l’icône  (rotation)
(rotation)
Cliquez d’abord sur le centre du dernier cercle (centre de la roue). Une boîte de dialogue vous demande l’angle de la rotation. Comme angle de la rotation, entrez -a/r puis validez comme ci-dessous :
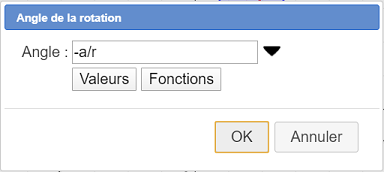
Nous utilisons ici la formule donnant la longueur d’un arc de cercle : $Long = r \times \vartheta$ où ici la longueur de l’arc est a. Mais n’oubliez pas le signe -.
Cliquez ensuite sur le point de la courbe de coordonnées (x ; f(x)).
Le point image qui apparaît représente la position actuelle du point de la roue qui était en bas de la roue quand la roue était au point d’abscisse 0.
Utilisez à nouveau l’icône de rotation  et cliquez sur le centre de la roue. Cette fois choisissez comme angle pi/3 (vous pouvez cliquez sur la flèche noire déroulant une liste des angles prédéfinis comme ci-dessous).
et cliquez sur le centre de la roue. Cette fois choisissez comme angle pi/3 (vous pouvez cliquez sur la flèche noire déroulant une liste des angles prédéfinis comme ci-dessous).
Cliquez sur le point précédemment créé. Cliquez à nouveau sur le dernier point et ainsi de suite 5 fois de suite pour avoir 6 points régulièrement espacés sur la roue.
Joignez ensuite ces points deux à deux opposés par des segments pour avoir les "rayons" de la roue comme cela :
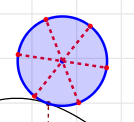
.
Vous pouvez déjà constater qu’en capturant le point mobile du curseur en haut et à gauche la roue tourne sans glissement sur la courbe.
Nous allons maintenant créer une macro qui va faire automatiquement tourner la roue.
Pour cela déroulez la barre d’outils des affichages et cliquez à sa droite sur l’icône  comme ci-dessous puis choisissez dans la liste Macro d’animation de point lié.
comme ci-dessous puis choisissez dans la liste Macro d’animation de point lié.

On vous demande d’abord de cliquer sur l’endroit où sera affichée la macro : cliquez en dessous du curseur.
Remplissez la boîte de dialogue qui apparaît comme ci-dessous :
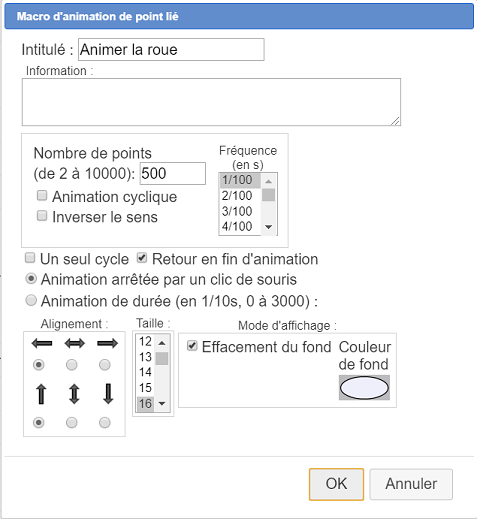
Maintenant pour lancer l’animation il n’y a plus qu’à activer dans la barre d’outil supérieure l’outil  et cliquer sur l’intitulé de la macro. Cliquez à nouveau sur la figure pour arrêter l’animation.
et cliquer sur l’intitulé de la macro. Cliquez à nouveau sur la figure pour arrêter l’animation.
En bas et à droite de la figure pour pouvez cliquer sur les boutons + et - pour faire varier le rayon de la roue.
Apportons une dernière amélioration à cette figure en y ajoutant une éditeur de formule qui permettra de modifier la formule de f(x) directement sur la figure.
Déroulez la barre d’outil des affichages et cliquez sur l’icône  .
.
Cliquez ensuite à l’endroit où sera affiché cet éditeur (par exemple en haut et au centre de la figure) et remplissez la boîte de dialogue comme ci-dessous puis validez :
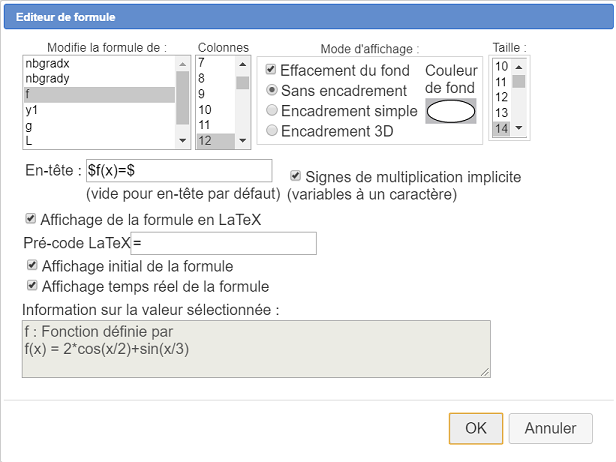
Vous pouvez maintenant changer la formule de la fonction f. Il vaut mieux que la fonction soit continue et pas trop irrégulière !
Voici ci-dessous le code Base 64 de cette figure :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAATeAAACygAAAQEAAAAAAAAAAAAAAGb#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAPQ1ZhcmlhYmxlQm9ybmVlAP####8AAXI#8AAAAAAAAD#QAAAAAAAAP#QAAAAAAAA#0AAAAAAAAAEABDAuMjUABDEuMjUABDAuMjX#####AAAAAQAKQ1BvaW50QmFzZQD#####AAAAAAAOAAFPAMAoAAAAAAAAAAAAAAAAAAAAAAUAAUB9QAAAAAAAQHINcKPXCj7#####AAAAAQAUQ0Ryb2l0ZURpcmVjdGlvbkZpeGUA#####wEAAAAAEAAAAQAAAAEAAAACAT#wAAAAAAAA#####wAAAAEAD0NQb2ludExpZURyb2l0ZQD#####AAAAAAEOAAFJAMAYAAAAAAAAAAAAAAAAAAAAAAUAAUA6AAAAAAAAAAAAA#####8AAAABAAlDRHJvaXRlQUIA#####wAAAAAAEAAAAQAAAAEAAAACAAAABP####8AAAABABZDRHJvaXRlUGVycGVuZGljdWxhaXJlAP####8AAAAAABAAAAEAAAABAAAAAgAAAAX#####AAAAAQAJQ0NlcmNsZU9BAP####8BAAAAAAAAAQAAAAIAAAAE#####wAAAAEAEENJbnREcm9pdGVDZXJjbGUA#####wAAAAYAAAAH#####wAAAAEAEENQb2ludExpZUJpcG9pbnQA#####wEAAAAAEAAAAQAABQABAAAACAAAAAoA#####wAAAAABDgABSgDAKAAAAAAAAMAQAAAAAAAAAAAFAAIAAAAI#####wAAAAIAB0NSZXBlcmUA#####wDm5uYAAAABAAAAAgAAAAQAAAAKAQEAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAA#####wAAAAEACkNVbml0ZXhSZXAA#####wAEdW5pdAAAAAv#####AAAAAQALQ0hvbW90aGV0aWUA#####wAAAAL#####AAAAAQAKQ09wZXJhdGlvbgMAAAABP#AAAAAAAAD#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAADP####8AAAABAAtDUG9pbnRJbWFnZQD#####AQAAAAAQAAJXIgEAAAEAAAAABAAAAA3#####AAAAAQAJQ0xvbmd1ZXVyAP####8AAAACAAAADv####8AAAABAAdDQ2FsY3VsAP####8AB25iZ3JhZHgAAjIwAAAAAUA0AAAAAAAAAAAAEgD#####AAduYmdyYWR5AAIyMAAAAAFANAAAAAAAAP####8AAAABABRDSW1wbGVtZW50YXRpb25Qcm90bwD#####ABRHcmFkdWF0aW9uQXhlc1JlcGVyZQAAABsAAAAIAAAAAwAAAAsAAAAQAAAAEf####8AAAABABNDQWJzY2lzc2VPcmlnaW5lUmVwAAAAABIABWFic29yAAAAC#####8AAAABABNDT3Jkb25uZWVPcmlnaW5lUmVwAAAAABIABW9yZG9yAAAACwAAAAwAAAAAEgAGdW5pdGV4AAAAC#####8AAAABAApDVW5pdGV5UmVwAAAAABIABnVuaXRleQAAAAv#####AAAAAQAQQ1BvaW50RGFuc1JlcGVyZQAAAAASAAAAAAAQAAABAAAFAAAAAAsAAAAPAAAAEwAAAA8AAAAUAAAAFwAAAAASAAAAAAAQAAABAAAFAAAAAAsAAAAOAAAAAA8AAAATAAAADwAAABUAAAAPAAAAFAAAABcAAAAAEgAAAAAAEAAAAQAABQAAAAALAAAADwAAABMAAAAOAAAAAA8AAAAUAAAADwAAABYAAAANAAAAABIAAAAXAAAADwAAABAAAAAQAAAAABIAAAAAABAAAAEAAAUAAAAAGAAAABoAAAANAAAAABIAAAAXAAAADwAAABEAAAAQAAAAABIAAAAAABAAAAEAAAUAAAAAGQAAABz#####AAAAAQAIQ1NlZ21lbnQAAAAAEgEAAAAAEAAAAQAAAAEAAAAYAAAAGwAAABgAAAAAEgEAAAAAEAAAAQAAAAEAAAAZAAAAHQAAAAUAAAAAEgEAAAAACwABVwDAFAAAAAAAAMA0AAAAAAAAAAAFAAE#3FZ4mrzfDgAAAB7#####AAAAAgAIQ01lc3VyZVgAAAAAEgAGeENvb3JkAAAACwAAACAAAAASAAAAABIABWFic3cxAAZ4Q29vcmQAAAAPAAAAIf####8AAAACABJDTGlldU9iamV0UGFyUHRMaWUBAAAAEgBmZmYAAAAAACAAAAAPAAAAEAAAACAAAAACAAAAIAAAACAAAAASAAAAABIABWFic3cyAA0yKmFic29yLWFic3cxAAAADgEAAAAOAgAAAAFAAAAAAAAAAAAAAA8AAAATAAAADwAAACIAAAAXAAAAABIBAAAAABAAAAEAAAUAAAAACwAAAA8AAAAkAAAADwAAABQAAAAaAQAAABIAZmZmAAAAAAAlAAAADwAAABAAAAAgAAAABQAAACAAAAAhAAAAIgAAACQAAAAlAAAABQAAAAASAQAAAAALAAFSAEAgAAAAAAAAwCAAAAAAAAAAAAUAAT#RG06BtOgfAAAAH#####8AAAACAAhDTWVzdXJlWQAAAAASAAZ5Q29vcmQAAAALAAAAJwAAABIAAAAAEgAFb3JkcjEABnlDb29yZAAAAA8AAAAoAAAAGgEAAAASAGZmZgAAAAAAJwAAAA8AAAARAAAAJwAAAAIAAAAnAAAAJwAAABIAAAAAEgAFb3JkcjIADTIqb3Jkb3Itb3JkcjEAAAAOAQAAAA4CAAAAAUAAAAAAAAAAAAAADwAAABQAAAAPAAAAKQAAABcAAAAAEgEAAAAAEAAAAQAABQAAAAALAAAADwAAABMAAAAPAAAAKwAAABoBAAAAEgBmZmYAAAAAACwAAAAPAAAAEQAAACcAAAAFAAAAJwAAACgAAAApAAAAKwAAACz#####AAAAAgAMQ0NvbW1lbnRhaXJlAAAAABIBZmZmAAAAAAAAAAAAQBgAAAAAAAAAAAAAACALAAH###8AAAABAAAAAAAAAAEAAAAAAAAAAAALI1ZhbChhYnN3MSkAAAAaAQAAABIAZmZmAAAAAAAuAAAADwAAABAAAAAgAAAABAAAACAAAAAhAAAAIgAAAC4AAAAcAAAAABIBZmZmAAAAAAAAAAAAQBgAAAAAAAAAAAAAACULAAH###8AAAABAAAAAAAAAAEAAAAAAAAAAAALI1ZhbChhYnN3MikAAAAaAQAAABIAZmZmAAAAAAAwAAAADwAAABAAAAAgAAAABgAAACAAAAAhAAAAIgAAACQAAAAlAAAAMAAAABwAAAAAEgFmZmYAwCAAAAAAAAA#8AAAAAAAAAAAAAAAJwsAAf###wAAAAIAAAABAAAAAQAAAAAAAAAAAAsjVmFsKG9yZHIxKQAAABoBAAAAEgBmZmYAAAAAADIAAAAPAAAAEQAAACcAAAAEAAAAJwAAACgAAAApAAAAMgAAABwAAAAAEgFmZmYAwBwAAAAAAAAAAAAAAAAAAAAAAAAALAsAAf###wAAAAIAAAABAAAAAQAAAAAAAAAAAAsjVmFsKG9yZHIyKQAAABoBAAAAEgBmZmYAAAAAADQAAAAPAAAAEQAAACcAAAAGAAAAJwAAACgAAAApAAAAKwAAACwAAAA0#####wAAAAEABUNGb25jAP####8AAWYAEzIqY29zKHgvMikrc2luKHgvMykAAAAOAAAAAA4CAAAAAUAAAAAAAAAA#####wAAAAIACUNGb25jdGlvbgQAAAAOA#####8AAAACABFDVmFyaWFibGVGb3JtZWxsZQAAAAAAAAABQAAAAAAAAAAAAAAeAwAAAA4DAAAAHwAAAAAAAAABQAgAAAAAAAAAAXgAAAAFAP####8BAAAAABAAAXgAAAAAAAAAAABACAAAAAAAAAAABQABv#5GMaUabogAAAAFAAAAGQD#####AAJ4MQAAAAsAAAA3AAAAEgD#####AAJ5MQAFZih4MSn#####AAAAAQAOQ0FwcGVsRm9uY3Rpb24AAAA2AAAADwAAADgAAAAXAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAsAAAAPAAAAOAAAAA8AAAA5#####wAAAAIADUNMaWV1RGVQb2ludHMA#####wAAAAAAAAABAAAAOgAAAfQAAQAAADcAAAAEAAAANwAAADgAAAA5AAAAOv####8AAAABAAhDRGVyaXZlZQD#####AAJmJwAAADYAAAAdAP####8AAWcAIGludGVncmFsZShzcXJ0KDErZicodCleMiksdCwwLHgp#####wAAAAEAFUNJbnRlZ3JhbGVEYW5zRm9ybXVsZQABdAAAAB4BAAAADgAAAAABP#AAAAAAAAD#####AAAAAQAKQ1B1aXNzYW5jZQAAACAAAAA8AAAAHwAAAAEAAAABQAAAAAAAAAAAAAABAAAAAAAAAAAAAAAfAAAAAAABeAAAABIA#####wABTAAFZygxNikAAAAgAAAAPQAAAAFAMAAAAAAAAAAAABIA#####wACTCcABmcoLTE2KQAAACAAAAA9#####wAAAAEADENNb2luc1VuYWlyZQAAAAFAMAAAAAAAAAAAAAMA#####wAAAAAAEAAAAEAIAAAAAAAAAAAAAAAAAAAAAAUAAEBFgAAAAAAAQD#XCj1wo9gAAAATAP####8AB0N1cnNldXIAAAAFAAAABQAAAAMAAAA#AAAAPgAAAEAAAAAEAAAAAEEBAAAAABAAAAEAAAABAAAAQAE#8AAAAAAAAAAAAAUBAAAAQQAAAAAAEAAAAMAIAAAAAAAAP#AAAAAAAAAAAAUAAEBtQAAAAAAAAAAAQgAAAA0AAAAAQQAAAEAAAAAOAwAAAA8AAAA#AAAADgEAAAAPAAAAPwAAAA8AAAA+AAAAEAAAAABBAQAAAAANAAJPMQDAEAAAAAAAAEAQAAAAAAAAAAAFAAAAAEMAAABEAAAADQAAAABBAAAAQAAAAA4DAAAADgEAAAABP#AAAAAAAAAAAAAPAAAAPwAAAA4BAAAADwAAAD4AAAAPAAAAPwAAABAAAAAAQQEAAAAADQACSTEAwAAAAAAAAABACAAAAAAAAAAABQAAAABDAAAARgAAABgBAAAAQQAAAAAAEAAAAQAAAAEAAABAAAAAQwAAAAUBAAAAQQAAAAABEAACazEAwAAAAAAAAABAAAAAAAAAAAAAAQABP+JTJTJTJTIAAABI#####wAAAAIAD0NNZXN1cmVBYnNjaXNzZQEAAABBAAFhAAAARQAAAEcAAABJ#####wAAAAEAD0NWYWxldXJBZmZpY2hlZQEAAABBAAAAAAAAAAAAAAAAAMAYAAAAAAAAAAAAAABJDwAB####AAAAAQAAAAIAAAABAAAAAAAAAAAAAyRhPQABJAIAAABK#####wAAAAIAEUNTb2x1dGlvbkVxdWF0aW9uAP####8AAXgAAXQAAAAOCAAAACAAAAA9AAAAHwAAAAAAAAAPAAAASgAAAA4BAAAAIAAAAD0AAAAfAAAAAAAAAA8AAABK#####wAAAAEADUNGb25jdGlvbjNWYXIAAAAADgcAAAAPAAAASgAAAAEAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAA8AAAA#AAAAKQAAAAAOBwAAAA8AAABKAAAAAQAAAAAAAAAAAAAADwAAAD4AAAABAAAAAAAAAAAAAAABP4R64UeuFHsAAAAXAP####8AfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAsAAAAPAAAATAAAAAEAAAAAAAAAAP####8AAAACAAZDTGF0ZXgA#####wB#AAAAv#AAAAAAAABAGAAAAAAAAAAAAAAATRIAAAAAAAEAAAAAAAAAAQAAAAAAAAAAAAF4AAAAFwD#####AH8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAALAAAADwAAAEwAAAAgAAAANgAAAA8AAABMAAAAGAD#####AH8AAAAQAAABAAABAQAAAE0AAABP#####wAAAAEACUNEcm9pdGVPbQD#####AQAA#wAQAAABAAABAQAAAAsAAABPAAAAIAAAADwAAAAPAAAATAAAAAcA#####wEAAP8AEAAAAQAAAQEAAABPAAAAUf####8AAAACAAlDQ2VyY2xlT1IA#####wEAAP8AAAEBAAAATwAAAA8AAAABAAAAAAkA#####wAAAFIAAABTAAAACgD#####AQAA#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABAAAAVAAAAAoA#####wAAAP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAgAAAFQAAAAIAP####8AAAD#AAAAAgAAAFYAAABP#####wAAAAEACUNSb3RhdGlvbgD#####AAAAVgAAACUAAAAOAwAAAA8AAABKAAAADwAAAAEAAAAQAP####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAE8AAABYAAAALQD#####AAAAVgAAAA4DAAAADwAAAAAAAAABQAgAAAAAAAAAAAAQAP####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFkAAABaAAAAEAD#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABbAAAAWgAAABAA#####wD#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAXAAAAFoAAAAQAP####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAF0AAABaAAAAEAD#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABeAAAAWgAAABgA#####wD#AAAAEAAAAQAAAQIAAABZAAAAXQAAABgA#####wD#AAAAEAAAAQAAAQIAAABbAAAAXgAAABgA#####wD#AAAAEAAAAQAAAQIAAABcAAAAX#####8AAAABAA5DU3VyZmFjZURpc3F1ZQD#####AAAA#wAAAAAABQAAAFf#####AAAAAgAXQ01hY3JvQW5pbWF0aW9uUG9pbnRMaWUA#####wAAAP8BAAD#####EEBFgAAAAAAAQFL1wo9cKPYCAe#v+wAAAAAAAAAAAAAAAQAAAAAAAAAAAA5BbmltZXIgbGEgcm91ZQAAAAAAAAoAAAH0AAAAAAAAAEkAAQD#####AAAABAAPQ0VkaXRldXJGb3JtdWxlAP####8AAAAAAQAA#####w5AdpAAAAAAAEA11wo9cKPYAAH###8AAAACAAAAAAAAAAEAAAAAAAAAAAAAADYAByRmKHgpPSQAAAAMAQEAAT0BAQAAAA###########w==