Toutes les versions de cet article : [English] [Español] [français]
Nous allons montrer dans cet article comment utiliser des constructions prédéfinies de MathGraph32 pour représenter des plans et autres objets dans l’espace.
Cet article a été adapté à la version JavaScript de MathGraph32.
Commencez par créer une figure pseudo 3D avec l’icône  , choisissez Figure 3D de base puis choisissez l’item Repère 3D orthonormal.
, choisissez Figure 3D de base puis choisissez l’item Repère 3D orthonormal.
Nous allons maintenant créer quatre curseurs qui contiendront les quatre paramètres de notre équation de plan $ax+by+cz+d=0$.
Cliquez sur l’icône  de création d’un curseur. Cliquez en haut et à gauche de la figure et renseignez la boîte de dialogue comme ci-dessous. Nous créons ici un curseur à valeurs entières dont les valeurs iront de -6 à +6.
de création d’un curseur. Cliquez en haut et à gauche de la figure et renseignez la boîte de dialogue comme ci-dessous. Nous créons ici un curseur à valeurs entières dont les valeurs iront de -6 à +6.
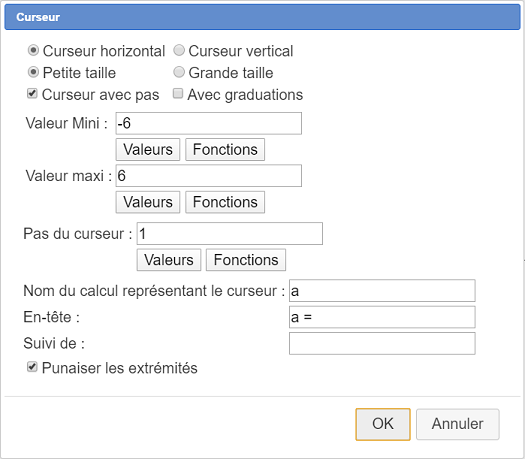
A noter : les extrémités du curseur sont punaisées par défaut. Si vous voulez le déplacer ou l’agrandir il vous faudra d’abord les dépunaiser avec l’outil  .
.
Créez de même trois autres curseurs à valeurs entières (entre -6 et +6) au-dessous du précédent pour les valeurs de b, c et d.
Avec la version JavaScript, les macro-constructions prédéfinies doivent être téléchargées séparément sur le site de MathGraph32 sur cette page Téléchargement de MathGraph32 version 7.9.
Cela a un avantage : vous pouvez y rajouter des macro-constructions que vous avez créées vous même ou supprimer des macro-constructions que vous jugez inutiles.
Nous supposerons donc que vous avez téléchargé la dernière version des constructions et que vous avez décompressé le fichier zip les contenant dans un dossier de votre choix.
Pour gérer les macro-constructions nous devons faire apparaître de nouvelles icônes dans la barre d’outils supérieure. Pour cela utilisez l’icône  .
.
Utilisez maintenant l’icône  (gestion des macro-constructions) et choisissez l’item Incorporer une construction depuis un fichier. Naviguez jusqu’au dossier contenant les constructions prédéfinies. Ouvrez le dossier Espace puis le sous-dossier Points et choisissez la construction Représentation plan par équation.
(gestion des macro-constructions) et choisissez l’item Incorporer une construction depuis un fichier. Naviguez jusqu’au dossier contenant les constructions prédéfinies. Ouvrez le dossier Espace puis le sous-dossier Points et choisissez la construction Représentation plan par équation.
Cette construction fait maintenant partie de votre figure. Pour le constater, utilisez l’icône  et choisissez l’item Modification des infos d’une construction.
et choisissez l’item Modification des infos d’une construction.
Cette construction attend quatre objets sources numériques qui sont a, b, c et d et quatre objets sources graphiques qui sont les points définissant notre repère de l’espace : 0, I, J et K.
Utilisez à nouveau l’icône  et choisissez l’item Implémenter une construction de la figure. Une boîte de dialogue s’ouvre et notre unique construction y est déjà sélectionnée. Cliquez sur le bouton Implémenter.
et choisissez l’item Implémenter une construction de la figure. Une boîte de dialogue s’ouvre et notre unique construction y est déjà sélectionnée. Cliquez sur le bouton Implémenter.
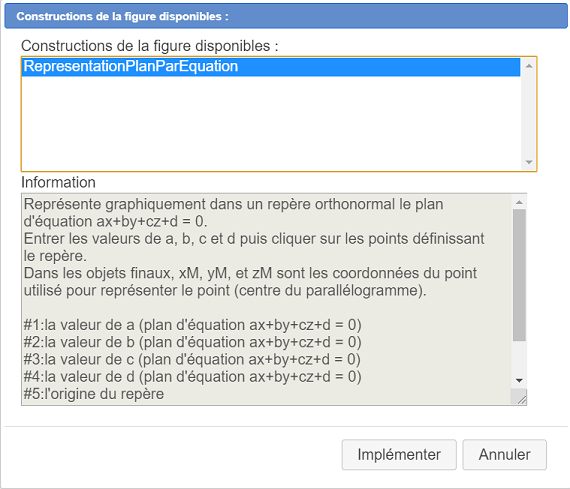
Nous devons maintenant indiquer à notre construction quels sont les objets sources.
Dans la liste de gauche cliquez sur le n°1. Dans la liste de droite associez lui le calcul a (créé lors de la création du premier curseur) comme ci-dessous :
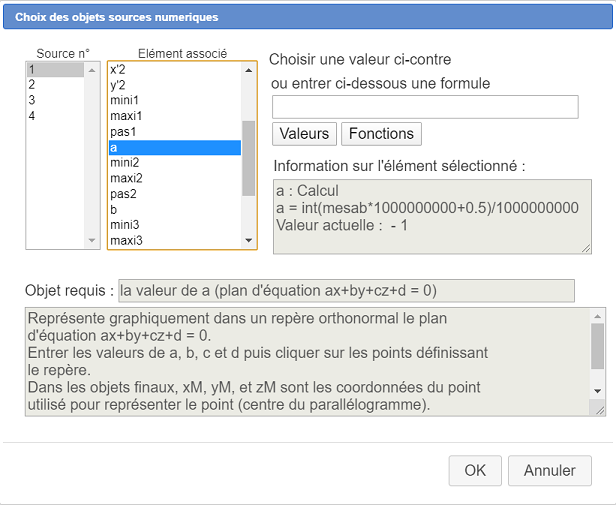
De même associez aux éléments 2, 3 et 4 les valeurs de b, c et d puis validez. En haut et à droite de la figure, un affichage fugitif vous demande maintenant de cliquer sur l’origine du repère : cliquez sur O. De même cliquez ensuite sur I, J et K.
Le plan est représenté par un parallélogramme de couleur bleue (il s’agit en fait d’un polygone qui a servi a créer une surface). Quatre points de contrôle permettent d’agrandir ou réduire ce polygone. Utilisez l’icône ![]() pour masquer le point créé au centre de ce polygone qui ne nous servira pas ici.
pour masquer le point créé au centre de ce polygone qui ne nous servira pas ici.
A l’aide de l’outil de capture ![]() modifiez les curseurs pour obtenir les mêmes valeurs que ci-dessous pour a, b, c et d (1, 1, 3 et 3) (la figure ci-dessous est dynamique et vous pouvez y modifier les valeurs de a, b, c et d). Vous pouvez aussi la faire tourner avec $\vartheta$.
modifiez les curseurs pour obtenir les mêmes valeurs que ci-dessous pour a, b, c et d (1, 1, 3 et 3) (la figure ci-dessous est dynamique et vous pouvez y modifier les valeurs de a, b, c et d). Vous pouvez aussi la faire tourner avec $\vartheta$.
Nous allons maintenant utiliser une construction permettant de créer le projeté orthogonal d’un point (ici l’origine) sur un plan (et de fournir ses coordonnées qui seront dans des calculs nommés xproj, yproj et zproj).
Utilisez à nouveau l’icône  et choisissez l’item Incorporer une construction depuis un fichier, ouvrez le dossier nommé Espace puis le sous-dossier Points et cliquez sur la construction nommée ProjeteOrthogonalPointSurPlan. Cliquez sur Ouvrir. comme ci-dessous :
et choisissez l’item Incorporer une construction depuis un fichier, ouvrez le dossier nommé Espace puis le sous-dossier Points et cliquez sur la construction nommée ProjeteOrthogonalPointSurPlan. Cliquez sur Ouvrir. comme ci-dessous :
Cette construction fait maintenant partie de notre figure.
Pour l’implémenter, utilisez à nouveau l’icône  et choisissez l’item Implémenter une construction de la figure.
et choisissez l’item Implémenter une construction de la figure.
Pour l’élément source n°1 (abscisse du point à projeter) entrez directement 0 (abscisse de l’origine) comme ci-dessous. Procédez de même avec les éléments sources 2 et 3 (valeurs 0).
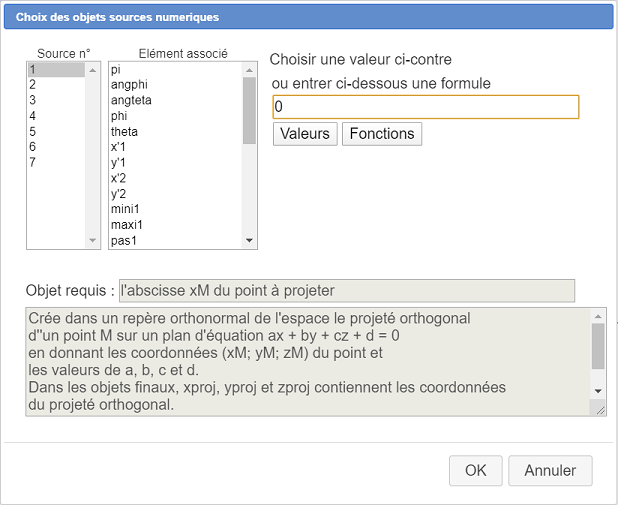
On nous demande comme élément source n° 4 la valeur de a : associez lui la valeur déjà existante comme ci-dessous :
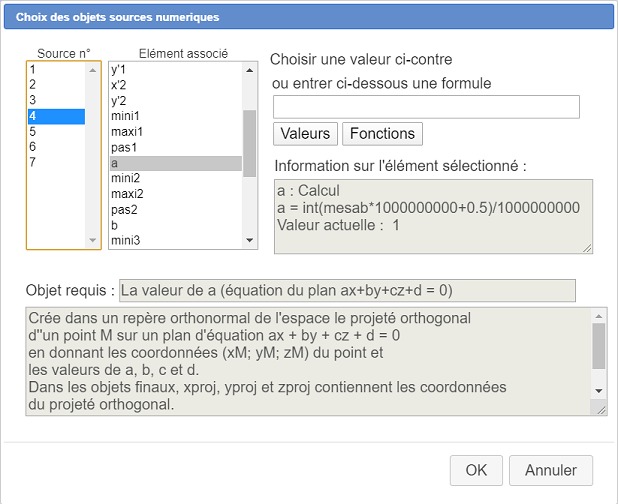
.
De même associez aux éléments sources 5, 6 et 7 les calculs déjà existants b, c et d .
En haut et à droite de la figure, un affichage fugitif demande ensuite de cliquer sur les quatre points définissant le repère : cliquez successivement sur O, I, J et K.
Un nouveau point apparaît et, dans les objets numériques, trois calculs nommés xproj, yproj et zproj contiennent les coordonnées de ce point (utilisez l’icône  pour voir tous les objets de type calculs créés). Nommez ce point H avec l’outil
pour voir tous les objets de type calculs créés). Nommez ce point H avec l’outil  .
.
Nous allons maintenant simuler un point lié à notre plan. Pour cela utilisez l’icône  . Cliquez d’abord sur le bord du plan (c’est en fait un polygone) puis à l’intérieur de ce polygône. Un nouveau point apparaît. Nommez le M.
. Cliquez d’abord sur le bord du plan (c’est en fait un polygone) puis à l’intérieur de ce polygône. Un nouveau point apparaît. Nommez le M.
Utilisons maintenant une construction prédéfinie très puissante qui va nous permettre de récupérer les coordonnées de notre point M sachant qu’il est dans un plan dont on connaît une équation.
Utilisez à nouveau l’icône  et choisissez l’item Incorporer une construction depuis un fichier, ouvrez le dossier nommé Espace puis le sous-dossier Points et cliquez sur la construction nommée Calcul Coordonnees Point Dans Plan. Cliquez sur Ouvrir.
et choisissez l’item Incorporer une construction depuis un fichier, ouvrez le dossier nommé Espace puis le sous-dossier Points et cliquez sur la construction nommée Calcul Coordonnees Point Dans Plan. Cliquez sur Ouvrir.
Dans la boîte de dialogue qui s’ouvre affectez comme précédemment les valeurs de a, b, c et d aux quatre objets sources 1, 2, 3 et 4.
On vous demande ensuite de cliquer sur le point dont on veut calculer les coordonnées : cliquez sur M. Cliquez ensuite comme indiqué sur les points O, I, J et K.
Utilisez l’icône  de la barre supérieure. Allez en bas de la liste des objets créés. Les derniers objets créés sont les calculs contenant les coordonnées de M et s’appellent donc xM2, yM2 et zM2 comme on le voit ci-dessous.
de la barre supérieure. Allez en bas de la liste des objets créés. Les derniers objets créés sont les calculs contenant les coordonnées de M et s’appellent donc xM2, yM2 et zM2 comme on le voit ci-dessous.
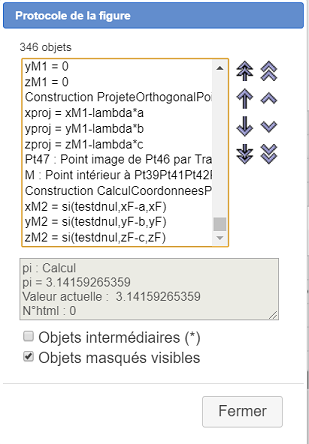
Nous allons maintenant créer un affichage LaTeX chargé d’afficher de façon dynamique ces trois coordonnées.
Cliquez sur l’icône  de création d’un affichage de code LaTeX libre et cliquez en haut de la figure à un endroit libre, sous les curseurs.
de création d’un affichage de code LaTeX libre et cliquez en haut de la figure à un endroit libre, sous les curseurs.
Dans la fenêtre qui apparaît, tapez la lettre M puis cliquez sur l’icône  . le code LaTeX correspondant à une parenthèse ouvrante apparaît :
. le code LaTeX correspondant à une parenthèse ouvrante apparaît : M\left( { } \right) et le curseur clignote à l’intérieur de l’accolade. Cliquez ensuite sur le bouton Insertion de valeur. Renseignez la boîte de dialogue comme ci-dessous :
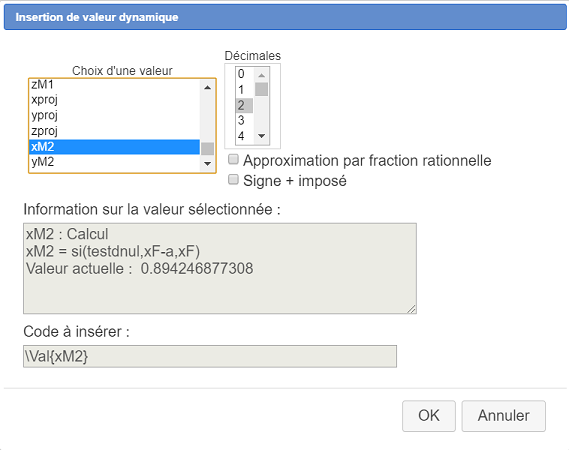
Validez. Juste après tapez un caractère point-virgule.
Le code LaTex est maintenant le suivant : M\left( {\Val{xM2}; } \right).
Utilisez ensuite de la même façon le bouton Insertion de valeur pour insérer un affichage des valeurs de xM2 et yM2 avec un point-virgule de séparation.
Procédez de même pour obtenir un affichage dynamique des valeurs de yM2 et zM2 après des points-virgules.
Pour le moment notre code LaTeX est :
M \left( \Val{xM2}; \Val{yM2}; \Val{zM2} \right).
Nous souhaitons que M ne soit pas affiché en italique : sélectionnez M dans l’éditeur puis cliquez sur l’icône 
Le code LaTeX est maintenant celui ci-dessous. Cochez les cases Effacement du fond et Encadrement simple.
\text{M} \left( \Val{xM2}; \Val{yM2}; \Val{zM2} \right)
Validez la boîte de dialogue. Notre affichage apparaît et si vous capturez M vous voyez ses coordonnées actualisées.
Procédez de même pour afficher dessous l’affichage LaTeX précédent l’affichage des coordonnées de H. Le code LaTeX obtenu doit être le suivant :
\text{H} \left( \Val{xproj}; \Val{yproj}; \Val{zproj} \right)
Nous allons maintenant demander au logiciel de calculer la distance entre O et M à l’aide d’une construction prédéfinie (on pourrait bien sûr les calculer directement).
Cette fois encore, utilisez l’icône  , choisissez l’item Incorporer une construction depuis un fichier et incorporez la construction nommée Distance Point Point que vous trouvez dans le dossier Espace -> Distances.
, choisissez l’item Incorporer une construction depuis un fichier et incorporez la construction nommée Distance Point Point que vous trouvez dans le dossier Espace -> Distances.
Puis utilisez de nouveau l’icône  et choisissez l’item Implémenter une construction de la figure. Choisissez cette dernière construction Distance Point Point dans la liste et cliquez sur le bouton Implémenter.
et choisissez l’item Implémenter une construction de la figure. Choisissez cette dernière construction Distance Point Point dans la liste et cliquez sur le bouton Implémenter.
Comme objets sources 1, 2 et 3, entrez directement comme formule 0 dans le champ d’édition (coordonnées de l’origine) et affectez comme objets sources 4, 5 et 6 respectivement xM2, yM2 et zM2 (coordonnées de M). Un objet final a été créé nommé dist qui contient la distance entre O et M. Vous pouvez le constater avec l’outil  de la barre supérieure.
de la barre supérieure.
Nous allons maintenant créer un affichage de cette valeur. Pour cela utilisez l’icône ![]() puis cliquez au-dessous des deux affichages précédents.
puis cliquez au-dessous des deux affichages précédents.
Renseignez la boîte de dialogue comme ci-dessous (vous pouvez utiliser le bouton Valeurs).
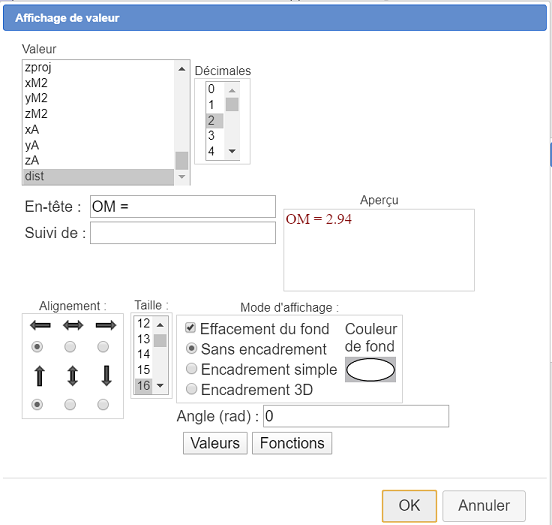
De le même façon utilisez la même construction prédéfinie pour calculer la distance entre O et H (rappelons que celles de H sont contenues dans xproj, yproj et zproj) et créez une affichage de cette valeur (dist1) au dessous de l’affichage précédent.
Notre figure est maintenant celle ci-dessous. Capturez $\theta$ pour faire tourner le figure, le point M ou faites varier les valeurs de a, b, c et d avec les curseurs.
Nous allons maintenant utiliser des constructions prédéfinies pour représenter la sphère de centre O et passant par M et le cercle d’intersection de celle-ci avec notre plan.
Cette fois encore, utilisez l’icône  , choisissez l’item Incorporer une construction depuis un fichier et incorporez la construction nommée Sphere Par Coord Centre Rayon que vous trouvez dans le dossier Espace -> Solides.
, choisissez l’item Incorporer une construction depuis un fichier et incorporez la construction nommée Sphere Par Coord Centre Rayon que vous trouvez dans le dossier Espace -> Solides.
Procédez de même pour incorporer dans la figure la construction Cercle Intersection Spere Plan que vous trouverez dans le dossier Droites Cercles.
Commençons par créer la sphère de centre O et passant par M.
Utilisez l’icône  , choisissez l’item Implémenter une construction de la figure. Choisissez la construction SphereParCoordCentreRayon et cliquez sur le bouton Implémenter.
, choisissez l’item Implémenter une construction de la figure. Choisissez la construction SphereParCoordCentreRayon et cliquez sur le bouton Implémenter.
Une boîte de dialogue s’ouvre pour le choix des objets sources numériques. Pour les trois premiers objets sources, affectez comme formule 0 (coordonnées de O). Affectez à l’objet source numéro 4 la valeur dist (distance de O à M) comme ci-dessous.
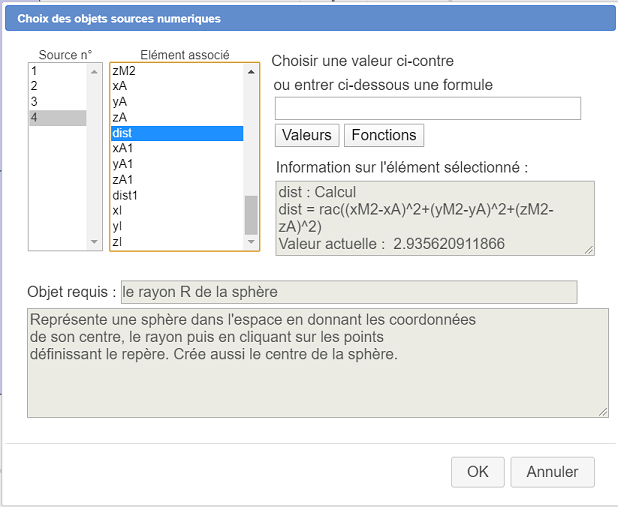
Il est ensuite demandé de cliquer sur les quatre points définissant le repère : cliquez sur O, I, J et K. La représentation de la sphère apparaît (elle est composée de lieux d’objets).
Représentons maintenant graphiquement le cercle d’intersection de la sphère avec le plan.
Utilisez l’icône  , choisissez l’item Implémenter une construction de la figure. Choisissez la construction CercleIntersectionSpherePlan et cliquez sur le bouton Implémenter.
, choisissez l’item Implémenter une construction de la figure. Choisissez la construction CercleIntersectionSpherePlan et cliquez sur le bouton Implémenter.
Affectez comme valeur pour les trois premiers objets sources 0 en utilisant le champ Formule (coordonnées du centre de la sphère). Comme élément associé à l’objet source n°4, cliquez sur dist. Comme éléments associés aux objets sources n°5, 6, 7 et 8 cliquez sur a, b, c et d. Validez.
Il est ensuite demandé de cliquer sur les quatre points définissant le repère : cliquez sur O, I, J et K (pour O choisissez point libre).
Un lieu de points apparaît représentant le cercle d’intersection.
Vous pouvez changer sa couleur et son style de trait avec l’outil  et le remplir de couleur avec l’outil
et le remplir de couleur avec l’outil 
Pour finir, activez le style de trait pointillé, 2 pixels d’épaisseurs, la couleur bleue et utilisez l’icône  pour joindre les points O, H et M par trois segments. Le triangle OHM est rectangle en H et H est le centre du cercle d’intersection.
pour joindre les points O, H et M par trois segments. Le triangle OHM est rectangle en H et H est le centre du cercle d’intersection.
Voici ci-dessous la figure finale :
Vous pouvez récupérer ci-dessous le code Base 64 de cette figure :