Los referenciales con MathGraph32 : Una gran versatilidad.

La versión 4.5 de MathGraph32 tiene una mayor versatilidad en el uso de los referenciales.

Recordemos ante todo que MathGraph32 permite el uso de múltiples referenciales en la misma figura. Podemos añadir un referencial a una figura haciendo clic sobre la herramienta .

Lo más simple es empezar con una figura en blanco provista de un referencial.

Para ello utilizamos el menú Archivo - Nueva figura con - Referencial sin vectores o Archivo - Nueva figura con - Referencial con vectores. En el segundo caso, dos vectores se añaden en cada eje (el nombre puede ser elegido en el cuadro de diálogo de creación de la nueva figura).

Observaciones : :
– Las graduaciones son en realidad lugares de objetos que se pueden capturar con la herramienta .

– El número de pasos de la graduación en cada eje puede ser modificado a posteriori, mediante el icono de modificación de un objeto numérico y luego modificando los cálculos designados nbgradx y nbgrady.

Ejemplo 1 : Utilización de una graduación trigonométrica

Ejemplo 2 : Creación de un referencial con una unidad sobre el eje (y’y) que sea el doble de la del eje (x’x)

Ejemplo 3 : Creación de un referencial con un desplazamiento del origen sobre uno de los ejes

Primer ejemplo : Utilización de una graduación trigonométrica

Deseamos trazar la gráfica de la función seno en un referencial ortogonal.

Para ello utilizamos el menú Archivo - Nueva figura con - Referencial sin vectores. En el cuadro de diálogo que aparece, seleccione el botón de opción Referencial ortogonal y, en la parte inferior del cuadro de diálogo, marcamos la casilla Graduación trigonométrica.

Una nueva figura aparece. El eje x se gradúa con múltiplos de $\pi$. Se pueden capturar sobre el eje de las abscisas y sobre el eje de las ordenadas los puntos de abscisa 1 y de ordenada 1 de manera de cambiar la unidad sobre cada eje.

Para trazar la curva representativa de la función seno, cliquear sobre el ícono . Un cuadro de diálogo se abre. Se rellena como se muestra a continuación y se valida. Por supuesto, se pueden añadir tantas curvas como uno quiera.

Segundo ejemplo : Creación de un referencial con unidad sobre el eje (y’y)

que sea el doble de la del eje (x’x)

.

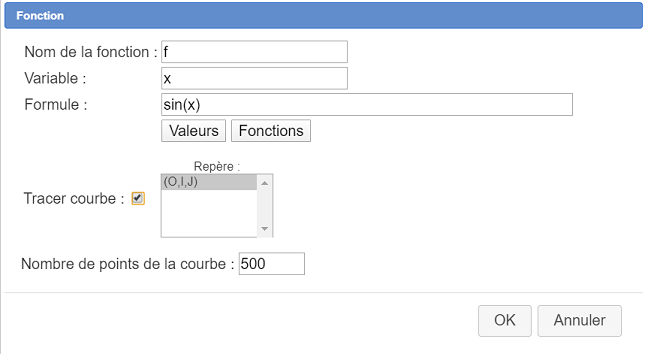
Deseamos crear una figura que dotada de un referencial cuya unidad será de 1 cm sobre el eje de las abscisas y 2 cm sobre el eje de las ordenadas

Para ello utilizamos el menú Archivo - Nueva figura con - Referencial sin vectores.

Completamos el cuadro de diálogo como se muestra a continuación.

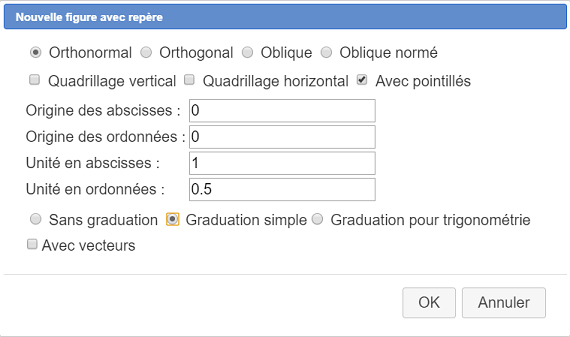
Se tiene a continuación la figura obtenida :

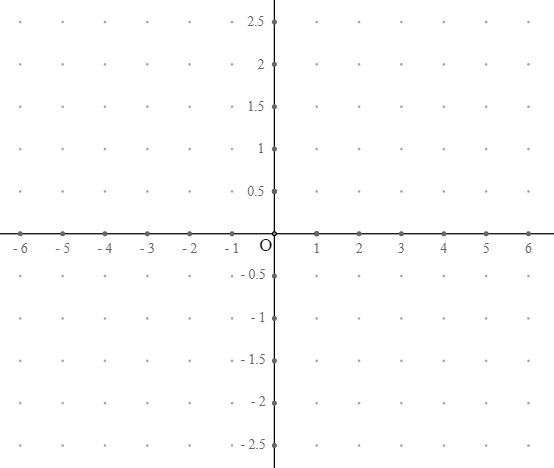
¿Cómo hacer para obtener un referencial graduado de la misma manera pero que solo tenga graduaciones sobre el eje de las ordenadas ?

Para ello la graduación del referencial debe ser ajustada posteriormente.

Utilizamos el menú Archivo - Nueva figura con - Referencial sin vectores como se observa a continuación (esta vez es necesario marcar el botón) Sin graduación :

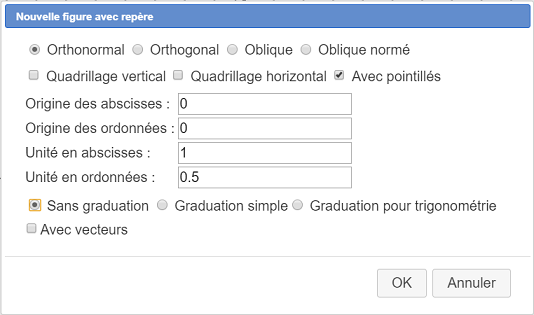
Utilizamos seguidamente el menú Modificar - Graduar los ejes de un referencial. Un cuadro de diálogo se abre. Se rellena como se muestra a continuación.

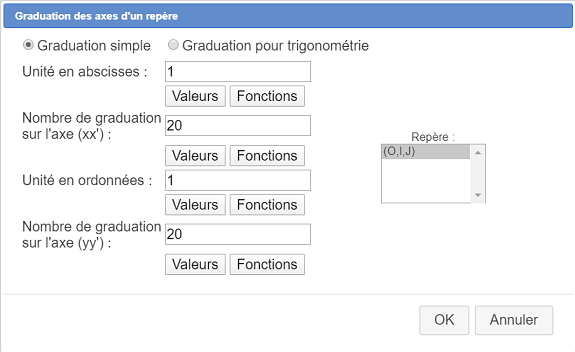
Se obtiene entonces una figura similar a la anterior pero con el eje de las ordenadas completamente graduado.

Ejemplo 3 : Creación de un referencial con un desplazamiento del origen sobre uno de los ejes

.

Queremos representar gráficamente las funciones f y g definidas sobre lel intervalo [0 ; 8] por $f(x)=600e^{-\frac{x}{10}}$ y $g(x)=400*exp(\frac{x}{20})-200$.

Utilizamos para ello el menú Archivo - Nueva figura con - Referencial sin vectores y completamos el cuadro de diálogo como se muestra a continuación :

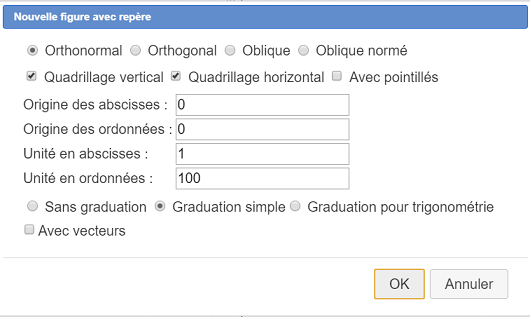
Utilizamos seguidamente la herramienta para desplazar el origen del referencial y llevarlo a la parte inferior izquierda de la ventana.

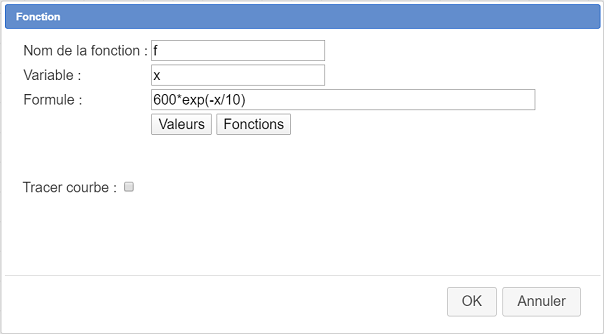
Para crear la función f cliqueamos sobre el ícono y completamos el cuadro de diálogo como se ve a continuación (Atención es necesario desmarcar la casilla Trazar curva) :

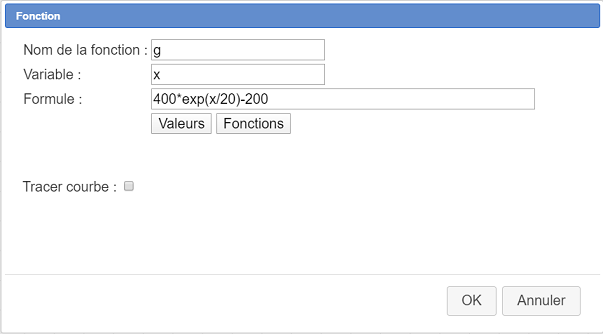
Del mismo modo creamos la función f con el ícono y completamos el cuadro de diálogo como se muestra a continuación :

Ahora vamos a trazar las curvas de estas dos funciones en el intervalo [0 ; 8].

Cliqueamos sobre el ícono .

La función f ya está seleccionado en la lista de la izquierda.

Marcamos la casilla ][a ; b][ que indica que queremos trazar la curva sobre un intervalo.

Completamos el cuadro de diálogo como se muestra a continuación :

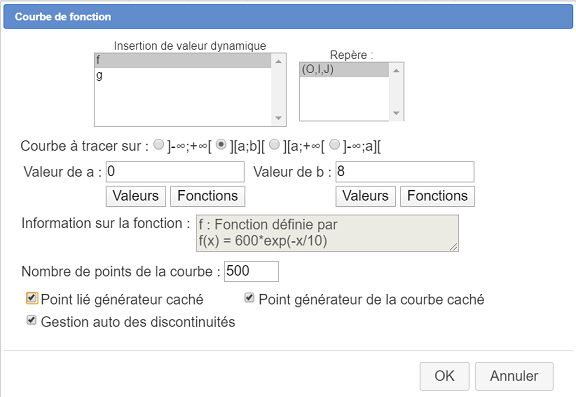
La curva de f aparece.

Cliqueamos sobre el ícono .

Esta vez cliqueamos sobre la función g en la lista de la izquierda.

Marcamos la casilla ][a ; b][ que indica que queremos trazar la curva sobre un intervalo.

Completamos el cuadro de diálogo como se muestra a continuación :

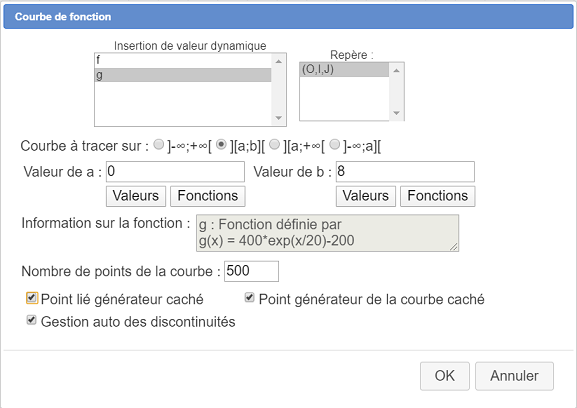
La curva de g aparece.

Le pedimos ahora a MathGraph32 calcular un valor aproximado de la solución de la ecuación f(x)=g(x).

Utilizamos para ello el menú Cálculos - Nuevo cálculo en R - Solución aproximada de ecuación. Un cuadro de diálogo se abre. Se completa como se muestra a continuación.

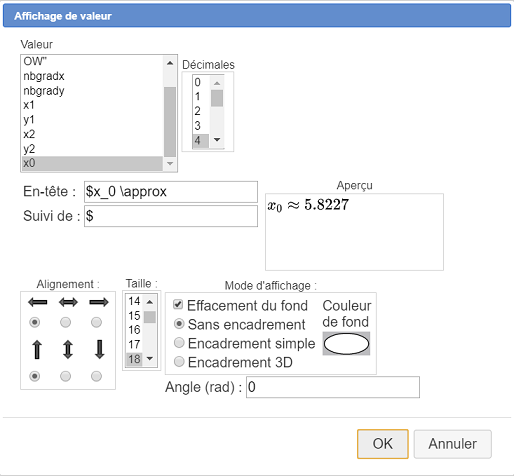
Visualizamos esta solución sobre la figura. Para ello cliqueamos sobre el ícono de visualización de valor. Cliqueamos en la parte superior izquierda de la figura. Completamos el cuadro de diálogo como se muestra a continuación y validamos :

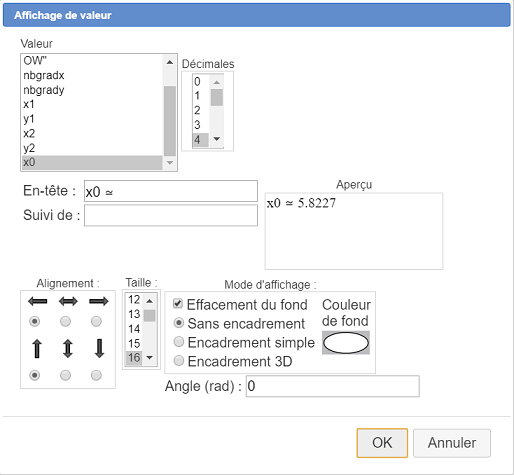
A continuación se muestra la figura obtenida. Podemos modificarla con el applet de construcción en línea de MathGraph32.

Finalmente, mostremos que se puede desplazar por ejemplo el origen de las ordenadas.

Utilizamos el siguiente menú Modificar - Referencial. El referencial (O,I,J), único referencial, ya está seleccionado. Cliqueamos sobre el botón Modificar.

En el campo Origen de las ordenadas en ingresamos 200 y validamos.