Toutes les versions de cet article : [English] [Español] [français]
Pour tester cet article vous devez avoir installé une version 7.0.0 ou ultérieure de MathGraph32.
MathGraph32 version 7.0 permet déjà de créer une droite de régression linéaire avec l’outil  : il suffit alors de cliquer sur des points puis sur le bouton rouge STOP pour obtenir la droite de régression linéaire de y par rapport à x.
: il suffit alors de cliquer sur des points puis sur le bouton rouge STOP pour obtenir la droite de régression linéaire de y par rapport à x.
Mais avoir une construction permettant d’obtenir cette droite de régression à partir d’une matrice peut être utilisé, par exemple pour l’utiliser dans des régressions non linéaires.
De plus ce sera un excellent exemple d’apprentissage sur MathGraph32, les macro constructions et les matrices.
Si vous souhaitez simplement utiliser les deux macro constructions (régression linéaire et exponentielle) vous pouvez les télécharger en fin de cet article.
Elles fonctionnent toutes les deux de la même façon : on leur fournit une matrice à deux colonnes (la première contient des abscisses de points et la deuxième des ordonnées) et la macro fournit les éléments nécessaires à la représentation graphique de la fonction de corrélation.
Créez une nouvelle figure vierge, par exemple munie d’un repère.
Nous allons créer une matrice de coordonnées très simple, ce qui nous permettra au besoin de vérifier que nous n’avons pas fait d’erreur dans nos formules.
Utilisez l’icône  située à la droite de la barre d’outils des calculs et choisissez l’item Matrice.
située à la droite de la barre d’outils des calculs et choisissez l’item Matrice.
Remplissez la boîte de dialogue comme ci-dessous.
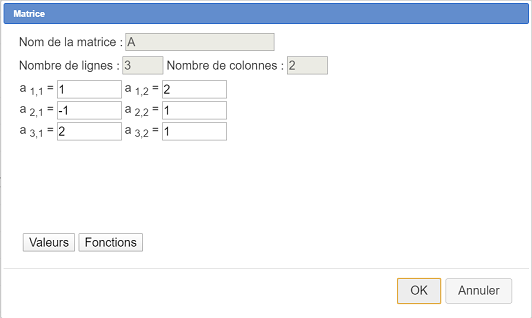
La première colonne contient les abscisses des points et la deuxième les ordonnées.
Dans nos calculs, nous ne devons pas utiliser 3 comme nombre de lignes de la matrice A car cette matrice sera remplacée par une autre quand la macro construction devra être implémentée.
Avec l’outil  créez donc le calcul réel suivant :
créez donc le calcul réel suivant :
| Nom du calcul | Formule | Commentaire |
| N | nbrow(A) | Dans un calcul réel, c’est le seul type de formule autorisé pour obtenir le nombre de lignes d’une matrice. Par exemple, 2*nbrow(A) ou nbrow(A+1) seraient des calculs réels refusés. |
Dans les calculs suivants nous allons utiliser la fonction somme qui fonctionne de la façon suivante :
somme(formule à sommer, nom variable sommation, indice de départ, indice de fin, pas)
Les trois derniers paramètres doivent être des entiers avec indice de début inférieur ou égal indice de fin et la valeur de pas doit être un entier supérieur ou égal à 1 (valeur 1 le plus souvent).
Créez donc les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
| mx | somme(A(k,1),k,1,N,1)/N | Contiendra la moyenne des abscisses $\overline{x}$. On utilise donc les termes de la première colonne de A. |
| my | somme(A(k,2),k,1,N,1)/N | Contiendra la moyenne des ordonnées $\overline{y}$. On utilise donc les termes de la deuxième colonne de A. |
| vx | somme(A(k,1)^2,k,1,N,1)/N-mx^2 | Contiendra la variance des x donnée par la formule $\overline{x^2}-(\overline{x})^2$ |
| vy | somme(A(k,2)^2,k,1,N,1)/N-my^2 | Contiendra la variance des y donnée par la formule $\overline{y^2}-(\overline{y})^2$ |
| covxy | somme(A(k,1)*A(k,2),k,1,N,1)/N-mx*my | Contiendra la covariance définie par la formule $\overline{xy}-\overline{x}\times\overline{y}$ |
| coefcor | covxy/(sqrt(vx)*sqrt(vy)) | Contiendra le coefficient de corrélation linéaire, compris entre 0 et 1. Plus il est proche de 1 meilleure sera la corrélation. |
| areg | covxy/vx | Coefficient directeur de la droite de corrélation linéaire |
| breg | my-areg*mx | L’ordonnée à l’origine de la droite de régression qui passe par le point de coordonnées $(\overline{x},\overline{y})$ |
A ce stade vous pouvez sauvegarder votre figure qui est prête pour créer notre macro construction.
Dans la barre d’outils supérieure cliquez sur l’icône ![]() qui fait apparaître des outils supplémentaires.
qui fait apparaître des outils supplémentaires.
L’icône  sert à créer la construction.
sert à créer la construction.
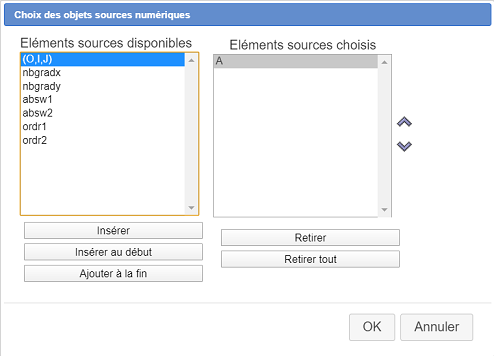
Cliquez une première fois sur cette icône et choisissez l’item Choix des objets sources numériques.
Une boîte de dialogue s’ouvre. Utilisez le bouton Insérer pour choisir comme seul objet source numérique la matrice A comme ci-dessous puis validez.
Notre macro-construction ne fournira que des objets finaux de type numérique.
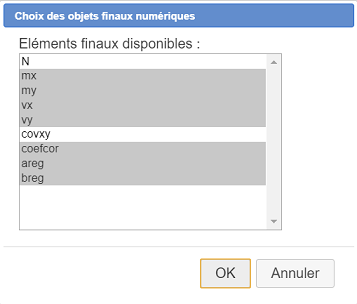
Cliquez une nouvelle fois sur l’icône  et choisissez l’item Choix des objets finaux numériques.
et choisissez l’item Choix des objets finaux numériques.
Sélectionnez les objets finaux numériques comme indiqué ci-dessous (vous pouvez aussi y inclure la covariance si vous le souhaitez) :
Cliquez une nouvelle fois sur l’icône  et choisissez l’item Finir la construction en cours.
et choisissez l’item Finir la construction en cours.
Remplissez la boîte de dialogue comme ci-dessous :
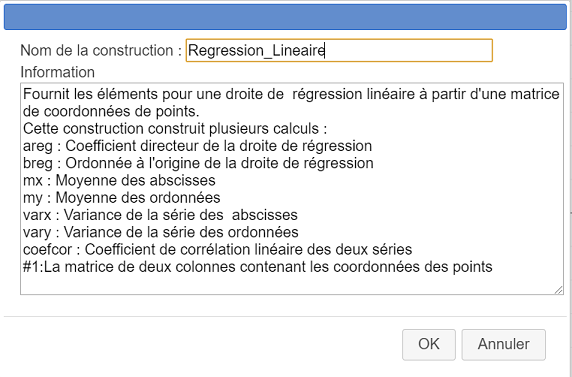
Voici le code à entrer dans le champ Information :
Fournit les éléments pour une droite de régression linéaire à partir d'une matrice de coordonnées de points.
Cette construction construit plusieurs calculs :
areg : Coefficient directeur de la droite de régression
breg : Ordonnée à l'origine de la droite de régression
mx : Moyenne des abscisses
my : Moyenne des ordonnées
varx : Variance de la série des abscisses
vary : Variance de la série des ordonnées
coefcor : Coefficient de corrélation linéaire des deux séries
#1:La matrice de deux colonnes contenant les coordonnées des pointsElle sert à donner des informations aux utilisateurs de notre macro-construction.
La dernière ligne commençant par #1 : fournit ce qui sera affiché comme indication quand l’utilisateur choisira le premier (et dernier) objet source de la construction.
Nous allons enregistrer notre macro construction dans un fichier séparé de façon à pouvoir l’utiliser dans d’autres figures.
Utilisez l’icône  (gestion des constructions) et choisissez l’item Enregistrer une construction de la figure.
(gestion des constructions) et choisissez l’item Enregistrer une construction de la figure.
Une boîte de dialogue s’ouvre. La seule construction est déjà sélectionnée. Cliquez sur le bouton Enregistrer et enregistrez votre construction dans le dossier de votre choix sous le nom Regression_Lineaire.mgc par exemple.
Enregistrez aussi votre figure sous le nom de votre choix (la macro construction en fait partie).
Nous allons maintenant tester le fonctionnement de notre construction dans une nouvelle figure.
Avec l’icône  , créez un figure munie d’un repère orthonormal.
, créez un figure munie d’un repère orthonormal.
Utilisez l’icône  (point libre) pour créer 6 points libres (vous pouvez en créer plus si vous le souhaitez).
(point libre) pour créer 6 points libres (vous pouvez en créer plus si vous le souhaitez).
Déroulez la barre d’outils des calculs, cliquez sur l’icône  et choisissez Matrice de coordonnées.
et choisissez Matrice de coordonnées.
Acceptez le nom fourni par défaut (mat) puis cliquez sur les 6 points. Pour finir cliquez sur le bouton rouge STOP en bas et à droite de la fenêtre.
MathGraph32 a pour vous :
Nous allons maintenant incorporer notre construction dans cette figure et l’appliquer à cette matrice.
Utilisez l’icône  (gestion des constructions) et choisissez l’item Incorporer une construction depuis un fichier.
(gestion des constructions) et choisissez l’item Incorporer une construction depuis un fichier.
Allez dans le dossier où vous avez enregistré votre fichier Regression_Lineaire.mgc , sélectionnez le et cliquez sur le bouton Ouvrir. La construction fait maintenant partie de votre figure.
Utilisez de nouveau l’icône  (gestion des constructions) et choisissez l’item Implémenter une construction de la figure.
(gestion des constructions) et choisissez l’item Implémenter une construction de la figure.
Notre unique construction est déjà sélectionnée. Cliquez sur le bouton Implémenter.
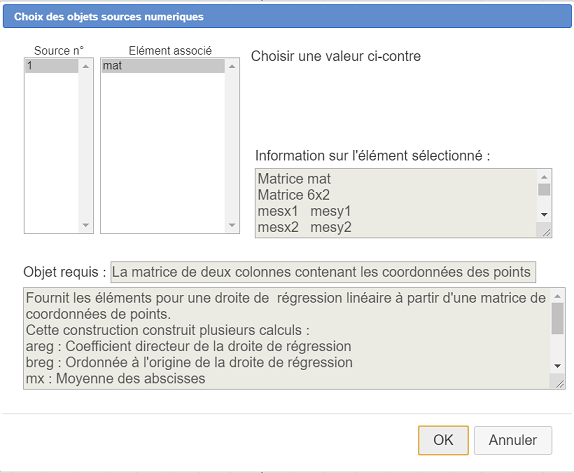
Une boîte de dialogue s’ouvre pour nous demander de choisir notre objet source (matrice). Affectez lui la matrice mat comme ci-dessous et validez :
Dans la barre d’outil du dessus, utiliser l’icône  pour voir les objets numériques de la figure.
pour voir les objets numériques de la figure.
En bas de la liste vous voyez les objets qui ont été créés par la construction, en particulier areg et breg.
Activez la couleur rouge, une épaisseur de trait de 2 pixels et activez l’outil  qui permet de créer une droite en donnant une équation de la droite dans un repère.
qui permet de créer une droite en donnant une équation de la droite dans un repère.
Comme formule pour l’équation de droite, entrez : y=areg*x+breg et validez comme ci-dessous :
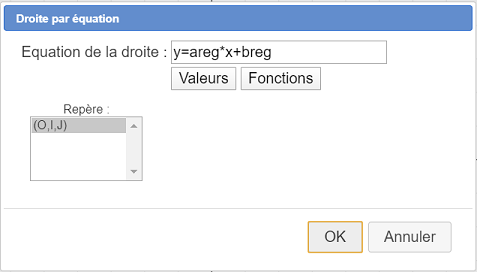
Votre droite de régression apparaît. Plus les points sont alignés plus la droite en est proche.
Nous allons maintenant créer une nouvelle figure qui nous permettra de créer une macro construction de régression exponentielle.
Utilisez l’icône  pour créer une nouvelle figure.
pour créer une nouvelle figure.
Utilisez l’icône  située à la droite de la barre d’outils des calculs et choisissez l’item Matrice.
située à la droite de la barre d’outils des calculs et choisissez l’item Matrice.
Créez la matrice nommée mat comme ci-dessous :
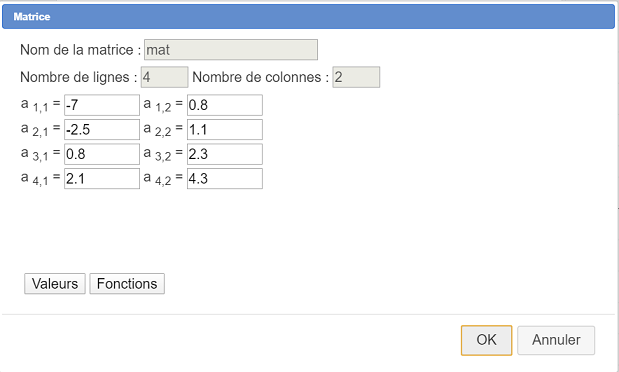
Puis utilisez l’icône  pour créer un calcul nommé N avec comme formule nbrow(mat).
pour créer un calcul nommé N avec comme formule nbrow(mat).
Rappelons d’abord le principe : si le nuage semble proche d’une courbe exponentielle, au lieu de l’approcher par régression linéaire (donc par une droite) on va chercher à l’approcher par une courbe dont l’équation est $y=A\times x^{ r}$ (on suppose que les ordonnées des points sont toutes positives).
Pour y > 0, $y=Ar^x$⇔$\ln (y)=\ln (A)+ \ln (x^r)$⇔$\ln (y)=\ln (A)+ x\ln (r) $.
En posant $y’=\ln{y}, \ln(A)=a$ et $\ln(r)=b$ la dernière égalité est donc de la forme $y’=ax+b$
L’idée est donc de construire une matrice à deux colonnes dont la première colonne est la même que celle de la matrice mat et la seconde formée des logarithmes népériens des nombres de la deuxième colonne de mat.
On appliquera à cette matrice notre macro construction de régression linéaire qui nous fournira les valeurs de areg et breg.
On en déduira les valeurs de $A=e^{areg}$ et $r=e^{breg}$
Construisons donc notre nouvelle matrice.
Utilisez l’icône  située à la droite de la barre d’outils des calculs et choisissez l’item Matrice par formule.
située à la droite de la barre d’outils des calculs et choisissez l’item Matrice par formule.
Remplissez la boîte de dialogue comme ci-dessous.
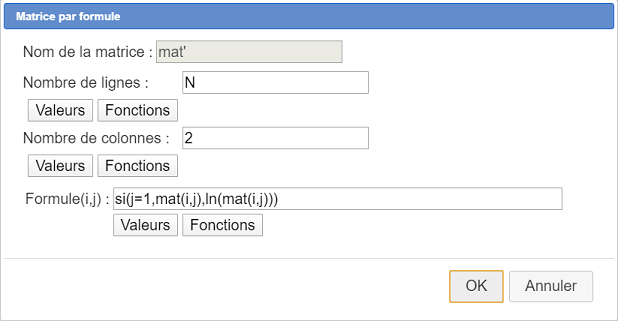
Voici la formule utilisée :
si(j=1,mat(i,j),ln(mat(i,j)))Utilisez l’icône  (gestion des constructions) et choisissez l’item Incorporer une construction depuis un fichier.
(gestion des constructions) et choisissez l’item Incorporer une construction depuis un fichier.
Allez dans le dossier où vous avez enregistré votre fichier Regression_Lineaire.mgc , sélectionnez le et cliquez sur le bouton Ouvrir.
Utilisez de nouveau l’icône  (gestion des constructions) et choisissez l’item Implémenter une construction de la figure.
(gestion des constructions) et choisissez l’item Implémenter une construction de la figure.
Notre unique construction est déjà sélectionnée. Cliquez sur le bouton Implémenter.
Remplissez la boîte de dialogue comme ci-dessous :
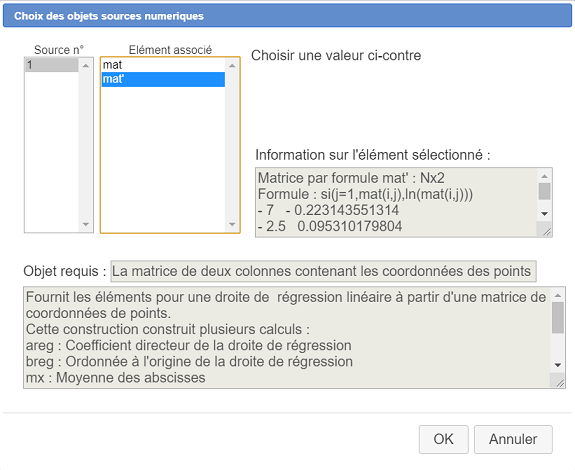
En utilisant l’icône  vous pouvez maintenant voir les objets créés par la macro construction, dont les calculs areg et breg.
vous pouvez maintenant voir les objets créés par la macro construction, dont les calculs areg et breg.
Utilisez maintenant l’icône  pour créer les calculs suivants
pour créer les calculs suivants
| Nom du calcul | Formule |
| A | exp(areg) |
| r | exp(breg) |
Créons maintenant la fonction qui fournira la formule d’approximation de y en x avec l’icône  comme ci-dessous (ne cochez pas la case Tracer la courbe)
comme ci-dessous (ne cochez pas la case Tracer la courbe)
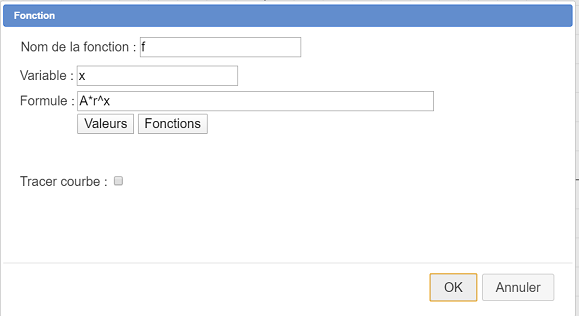
| Nom de la fonction | Formule |
| f | A*r^x |
Notre figure est maintenant prête pour créer notre nouvelle macro construction de régression exponentielle.
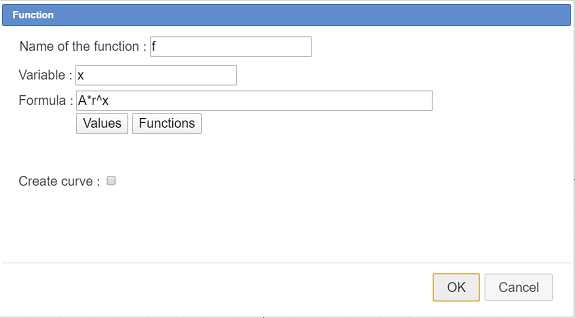
Activez l’outil  de création de construction et choisissez l’item Choix des objets sources numériques.
de création de construction et choisissez l’item Choix des objets sources numériques.
Comme seul élément source choisissez la matrice mat comme ci-dessous :
Activez de nouveau outil  et choisissez l’item Choix des objets finaux numériques.
et choisissez l’item Choix des objets finaux numériques.
Sélectionnez comme ci-dessous coefcor (coefficient de corrélation), A, r et f :
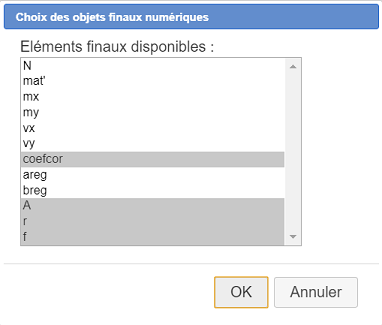
Activez de nouveau outil  et choisissez l’item Finir la construction en cours.
et choisissez l’item Finir la construction en cours.
Remplissez la boîte de dialogue comme ci-dessous :
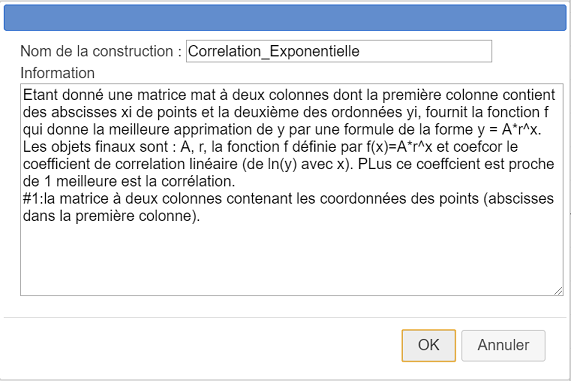
Voici le contenu du champ Information :
Etant donné une matrice mat à deux colonnes dont la première colonne contient des abscisses xi de points et la deuxième des ordonnées yi, fournit la fonction f qui donne la meilleure approximation de y par une formule de la forme y = A*r^x.
Les objets finaux sont : {A}, {r}, la fonction {f} définie par f(x)=A*r^x et coefcor le coefficient de corrélation linéaire (de ln(y) avec x). Plus ce coefficient est proche de 1 meilleure est la corrélation.
#1:la matrice à deux colonnes contenant les coordonnées des points (abscisses dans la première colonne).Votre nouvelle macro construction fait partie de votre figure.
Pour la sauver dans un fichier de suffixe mgc, utilisez l’icône  de gestion des constructions et choisissez l’item
de gestion des constructions et choisissez l’item
Enregistrer une construction de la figure. Enregistrez la sous le nom Regression_Exponentielle.mgc.
Il est préférable aussi de sauvegarder la figure elle-même des fois que vous ayez fait une erreur lors de la création de la macro construction.
Nous allons maintenant tester notre macro construction dans une autre figure.
Créez une nouvelle figure munie d’un repère et avec l’outil  créez quelques points libres comme ci-dessous de façon qu’ils soient "proches" d’une courbe exponentielle.
créez quelques points libres comme ci-dessous de façon qu’ils soient "proches" d’une courbe exponentielle.
Nous allons maintenant demander à MathGraph32 de créer une matrice dont les coordonnées soient celles des points créés.
Déroulez la barre d’outils des calculs, cliquez sur l’icône  et choisissez l’item Matrice de coordonnées.
et choisissez l’item Matrice de coordonnées.
Acceptez le nom mat comme nom de la matrice puis cliquez sur les points créés. Quand vous avez cliqué sur le dernier point, cliquez sur le bouton rouge STOP et bas et à droite de la fenêtre.
Si vous utilisez l’outil  vous verrez que MathGraph32 a mesuré l’abscisse et l’ordonnée de chaque point puis créé une matrice mat formée de ces mesures.
vous verrez que MathGraph32 a mesuré l’abscisse et l’ordonnée de chaque point puis créé une matrice mat formée de ces mesures.
Incorporons maintenant dans cette figure notre macro construction de régression exponentielle.
Utilisez l’icône  et choisissez l’item Incorporer une construction depuis un fichier.
et choisissez l’item Incorporer une construction depuis un fichier.
Allez chercher votre construction dans le dossier où vous l’avez enregistrée, sélectionnez là et cliquez sur le bouton Ouvrir. La construction fait maintenant partie de la figure.
Utilisez à nouveau l’icône  et choisissez l’item Implémenter une construction de la figure. Choisissez la construction de régression exponentielle et cliquez sur le bouton Implémenter.
et choisissez l’item Implémenter une construction de la figure. Choisissez la construction de régression exponentielle et cliquez sur le bouton Implémenter.
Une boîte de dialogue s’ouvre pour choisir le seul objet source requis, une matrice. Remplissez la comme ci-dessous en choisissant comme objet source la matrice mat et validez.
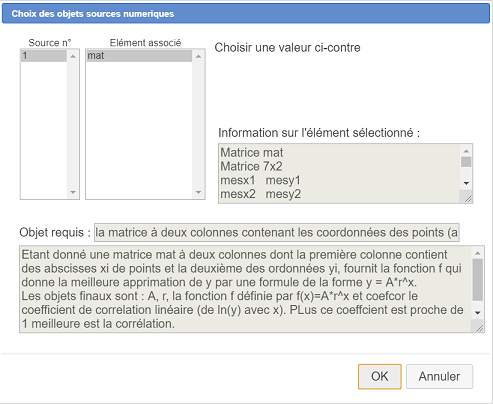
Dans la barre d’outil du dessus, utiliser l’icône  pour voir les objets numériques de la figure.
pour voir les objets numériques de la figure.
En bas de la liste vous voyez les objets qui ont été créés par la construction, coefcor, A, r et la fonction f.
Traçons maintenant la courbe représentative de f.
Dans la palette des couleurs, activez la couleur rouge puis utilisez l’outil  .
.
Demandez la courbe de la fonction f à tracer sur R.
Pour finir affichons la valeur du coefficient de corrélation à l’aide de l’outil d’affichage de valeur  .
.
Cliquez en haut et à gauche de la figure et remplissez la boîte de dialogue comme ci-dessous :
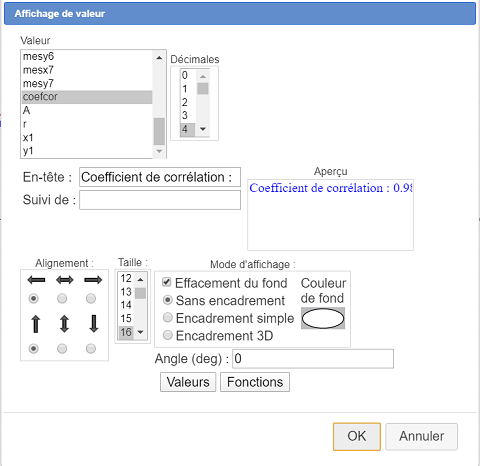
Vous pouvez maintenant capturer les points de la figure et constater que plus les points sont éloignés de la courbe moins le coefficient de corrélation est proche de 1.
Voici ci-dessous la figure finale :
Vous pouvez télécharger ces deux macro constructions dans des fichiers zip ci-dessous :